Chuyên đề: Ôn thi vào cấp 3 - Một số bài tập: Rút gọn biểu thức

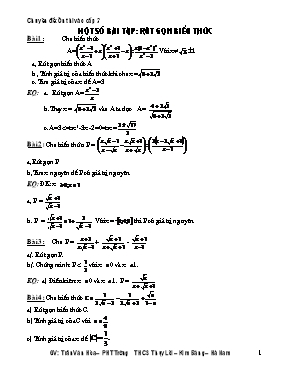
Mét sè bµi tËp: Rót gän biÓu thøc
Bµi 1 : Cho biÓu thøc 
 A=Víi x¹;±1
 a, Rót gän biÓu thøc A
 b , TÝnh gi¸ trÞ cña biÓu thøc khi cho x=
 c. T×m gi¸ trÞ cña x ®Ó A=3
KQ: 	a. Rót gän A=
b.Thay x= vµo A ta ®­îc A= 
c.A=3 x2-3x-2=0=> x=
Bµi 2: Cho biÓu thøc: P = 
a,Rót gän P
b,T×m x nguyªn ®Ó P cã gi¸ trÞ nguyªn.
KQ: §K: x 
a, P = 
b. P = . Víi x= th× P cã gi¸ trÞ nguyªn.
Bµi 3: Cho P = + - 
a/. Rót gän P.
b/. Chøng minh: P < víi x 0 vµ x 1.
KQ: a) §iÒu kiÖn: x 0 vµ x 1. P = 	
Bµi 4: Cho biÓu thøc 
a) Rót gän biÓu thøc C.
b) TÝnh gi¸ trÞ cña C víi .
c) TÝnh gi¸ trÞ cña x ®Ó 
Bµi 5: Cho biÓu thøc A = 
a)Nªu ®iÒu kiÖn x¸c ®Þnh vµ rót gän biÓu thøc A.
 b)T×m tÊt c¶ c¸c gi¸ trÞ cña x sao cho A < 0.
 c)T×m tÊt c¶ c¸c gi¸ trÞ cña tham sè ®Ó ph­¬ng tr×nh A cã nghiÖm.
Bài 6. Cho A = 
 a)Rút gọn A
 b)Tính giá trị của A khi a = 
 c)Tìm a để A < 0
Bài 7. Cho P = 
a) Rút gọn P
b) Tính giá trị của P tại x = 
c) Tìm x thỏa mãn 
Bài 8. Cho A = 
a) Rút gọn A
b) Tìm x Z để A Z
Bài 9. Cho P = 
a) Rút gọn P
b) Tìm a để 
Bµi 10 Cho biÓu thøc: P = 
a) T×m ®iÒu kiÖn cña a ®Ó P x¸c ®Þnh.
b) Rót gän P.
c) T×m c¸c gi¸ trÞ cña a ®Ó P > 0 và P < 0.
Câu 11: Cho biểu thức: 
a). Tìm điều kiện xác định của P? Rút gọn P.
b) Tìm x để 
Câu 12: Cho biểu thức 
a) Tìm điều kiện xác định của A? Rút gọn A.
b) Tính giá trị của biểu thức A khi x = 
c) Tìm x để A < 8. 
Bµi 13: Cho biÓu thøc 
a) T×m ®iÒu kiÖn x¸c ®Þnh, rót gän biÓu thøc A
b) Víi gi¸ trÞ nµo cña xth× A > 
c) T×m x ®Ó A ®¹t gi¸ trÞ lín nhÊt
Bµi 14: Cho biÓu thøc 
a) Nªu ®iÒu kiÖn x¸c ®Þnh vµ rót gän biÓu thøc P
b) T×m c¸c gi¸ trÞ cña x ®Ó P = 
c) T×m gi¸ trÞ nhá nhÊt cña biÓu thøc: M
Bµi 15: Cho biÓu thøc: 
a) T×m §KX§ , rót gän P
b) T×m gi¸ trÞ nhá nhÊt cña P
c) T×m x ®Ó biÓu thøc nhËn gi¸ trÞ nguyªn.
Bµi 16: Cho biÓu thøc: 
a) T×m §KX§, rót gän P.
b) T×m x ®Ó P <
Bµi 17: Cho biÓu thøc: 
a) T×m §KX§ vµ rót gän A
b) T×m tÊt c¶ c¸c gi¸ trÞ cña x sao cho A < 0
c) T×m tÊt c¶ c¸c gi¸ trÞ cña tham sè m ®Ó ph­¬ng tr×nh A. cã nghiÖm.
Bµi 18: Cho biÓu thøc: 
a) T×m §KX§, rót gän biÓu thøc A
b) TÝnh gi¸ trÞ cña biÓu thøc A
c) Víi gi¸ trÞ nµo cña x th× 
Bµi 19: Cho biÓu thøc : 
 P = 
a)T×m TX§ råi Rót gän 
b)T×m x ®Ó P =2 
c)TÝnh gi¸ trÞ cña P khi x = 3-2
Bµi 20: Cho biÓu thøc 
 	P= (
a)T×m TX§ råi rót gän P 
b)T×m a ®Ó P d­¬ng 
c)TÝnh gi¸ trÞ cña biÓu thøc biÕt a= 9- 4
Chuùc caùc em hoïc toát!
Mét sè bµi tËp: hµm sè bËc nhÊt – hµm sè bËc hai
HÖ hai ph­¬ng tr×nh bËc nhÊt hai Èn.
Bµi tËp 1: cho parabol y= 2x2. (p)
a. t×m hoµnh ®é giao ®iÓm cña (p) víi ®­êng th¼ng y= 3x-1.
b. t×m to¹ ®é giao ®iÓm cña (p) víi ®­êng th¼ng y=6x-9/2.
c. t×m gi¸ trÞ cña a,b sao cho ®­êng th¼ng y=ax+b tiÕp xóc víi (p) vµ ®i qua A(0;-2).
d. t×m ph­¬ng tr×nh ®­êng th¼ng tiÕp xóc víi (p) t¹i B(1;2).
e. biÖn luËn sè giao ®iÓm cña (p) víi ®­êng th¼ng y=2m+1. 
f. cho ®­êng th¼ng (d): y=mx-2. T×m m ®Ó :
+(p) kh«ng c¾t (d).	+(p)tiÕp xóc víi (d). t×m to¹ ®é ®iÓm tiÕp xóc ®ã?
+ (p) c¾t (d) t¹i hai ®iÓm ph©n biÖt.	+(p) c¾t (d).
Bµi tËp 2: cho hµm sè (p): y=x2 vµ hai ®iÓm A(0;1) ; B(1;3).
a. viÕt ph­¬ng tr×nh ®­êng th¼ng AB. t×m to¹ ®é giao ®iÓm AB víi (P) ®· cho.
b. viÕt ph­¬ng tr×nh ®­êng th¼ng d song song víi AB vµ tiÕp xóc víi (P).
c. viÕt ph­¬ng tr×nh ®­êng th¼ng d1 vu«ng gãc víi AB vµ tiÕp xóc víi (P).
d. chøng tá r»ng qua ®iÓm A chØ cã duy nhÊt mét ®­êng th¼ng c¾t (P) t¹i hai ®iÓm ph©n biÖt C,D sao cho CD=2.
Bµi tËp 3: Cho (P): y=x2 vµ hai ®­êng th¼ng a,b lÇn l­ît lµ: y= 2x-5;	y=2x+m
a. chøng tá r»ng ®­êng th¼ng a kh«ng c¾t (P).
b. t×m m ®Ó ®­êng th¼ng b tiÕp xóc víi (P), víi m t×m ®­îc h·y:
+ Chøng minh c¸c ®­êng th¼ng a,b song song víi nhau.
+ t×m to¹ ®é tiÕp ®iÓm A cña (P) víi b.
+ LËp pt ®t (d) ®i qua A vµ cã hÖ sè gãc b»ng -1/2. t×m to¹ ®é giao ®iÓm cña (a) vµ (d).
Bµi tËp 4 : cho hµm sè y=2x2 (P) vµ y=3x+m (d)
a. Khi m=1, t×m to¹ ®é c¸c giao ®iÓm cña (P) vµ (d).
b. TÝnh tæng b×nh ph­¬ng c¸c hoµnh ®é giao ®iÓm cña (P) vµ (d) theo m.
c. T×m mèi quan hÖ gi÷a c¸c hoµnh ®é giao ®iÓm cña (P) vµ (d) ®éc lËp víi m.
Bµi tËp 5: cho hµm sè y=-x2 (P) vµ ®­êng th¼ng (d) ®I qua N(-1;-2) cã hÖ sè gãc k.
a. chøng minh r»ng víi mäi gi¸ trÞ cña k th× ®­êng th¼ng (d) lu«n c¾t ®å thÞ (P) t¹i hai ®iÓm A,B. t×m k cho A,B n»m vÒ hai phÝa cña trôc tung.
b. gäi (x1;y1); (x2;y2) lµ to¹ ®é cña c¸c ®iÓm A,B, t×m k ®ÓS=x1+y1+x2+y2 ®¹t GTLN.
Bµi tËp 6: cho hµm sè y=x2 (P) vµ y=2mx-m2+4 (d)
a.t×m hoµnh ®é cña c¸c ®iÓm thuéc (P) biÕt tung ®é cña chóng y=(1- )2.
b.chøng minh r»ng (P) víi (d) lu«n c¾t nhau t¹i 2 ®iÓm ph©n biÖt. t×m to¹ ®é giao ®iÓm cña chóng. víi gi¸ trÞ nµo cña m th× tæng c¸c tung ®é cña chóng ®¹t gi¸ trÞ nhá nhÊt.
Bµi tËp 7: cho hµm sè y= mx-m+1 (d).
a. Chøng tá r»ng khi m thay ®æi th× ®t (d) lu«n ®i qua ®iÓm cè ®Þnh. t×m ®iÓm cè ®Þnh Êy.
b. T×m m ®Ó (d) c¾t (P) y=x2 t¹i 2 ®iÓm ph©n biÖt A vµ B, sao cho AB= .
Bµi tËp 8 : trªn hÖ trôc to¹ ®é Oxy cho c¸c ®iÓm M(2;1); N(5;-1/2) vµ ®t (d) y=ax+b.
a. T×m a vµ b ®Ó ®­êng th¼ng (d) ®i qua c¸c ®iÓm M, N.
b. X¸c ®Þnh to¹ ®é giao ®iÓm cña ®­êng th¼ng MN víi c¸c trôc Ox, Oy.
Bµi tËp 9: Cho hµm sè y=x2 (P) vµ y=3x+m2 (d).
a. Chøng minh víi bÊt kú gi¸ trÞ nµo cña m ®t (d) lu«n c¾t (P) t¹i 2 ®iÓm ph©n biÖt.
b. Gäi y1, y2 lµ c¸c tung ®é giao ®iÓm cña (d) vµ (P) t×m m ®Ó cã bthøc y1+y2= 11y1.y2
Bµi tËp 9: Cho hµm sè y=x2 (P).
a. VÏ ®å thÞ hµm sè (P).
b. Trªn (P) lÊy 2 ®iÓm A, B cã hoµnh ®é lÇn l­ît lµ 1 vµ 3. h·y viÕt ph­¬ng tr×nh ®­êng th¼ng AB.
c. LËp ph­¬ng tr×nh ®­êng trung trùc (d) cña ®o¹n th¼ng AB.
d. T×m to¹ ®é giao ®iÓm cña (d) vµ (P).
Bµi tËp 10: 
a. ViÕt ph­¬ng tr×nh ®­êng th¼ng tiÕp xóc víi (P) y=2x2 t¹i ®iÓm A(-1;2).
b. Cho hµm sè y=x2 (P) vµ B(3;0), t×m pt tho¶ m·n ®iÒu kiÖn tiÕp xóc víi (P) vµ ®i qua B.
c. Cho (P) y=x2. lËp ph­¬ng tr×nh ®­êng th¼ng ®i qua A(1;0) vµ tiÕp xóc víi (P).
d. Cho (P) y=x2 . lËp ph­¬ng tr×nh (d) song song víi ®t y=2x vµ tiÕp xóc víi (P).
e. ViÕt pt ®th¼ng song song víi ®t y=-x+2 vµ c¾t (P) y=x2 t¹i ®iÓm cã hoµnh ®é b»ng (-1)
f. ViÕt pt ®th¼ng vu«ng gãc víi (d) y=x+1 vµ c¾t (P) y=x2 t¹i ®iÓm cã tung ®é b»ng 9.
Bµi tËp 11 : Cho hÖ ph­¬ng tr×nh 
a) Gi¶i hÖ ph­¬ng tr×nh khi m = 1
b) Víi gi¸ trÞ nµo cña m th× hÖ ph­¬ng tr×nh nhËn cÆp sè ( x= 1 ; y =- 6) lµm nghiÖm
c) T×m m ®Ó hÖ ph­¬ng tr×nh cã nghiÖm duy nhÊt. T×m nghiÖm ®ã.
Bµi tËp 12 : Cho hÖ ph­¬ng tr×nh 
a) Gi¶i hÖ ph­¬ng tr×nh khi a = 1
b) T×m a ®Ó hÖ ph­¬ng tr×nh cã nghiÖm duy nhÊt vµ t×m nghiÖm ®ã. hÖ ph­¬ng tr×nh VN 
Bµi tËp 13 : Cho hÖ ph­¬ng tr×nh 
a) Gi¶i hÖ ph­¬ng tr×nh khi a = -2
b) T×m a ®Ó hÖ ph­¬ng tr×nh cã nghiÖm duy nhÊt, khi ®ã tÝnh x ; y theo a
c) T×m a ®Ó hÖ ph­¬ng tr×nh cã nghiÖm duy nhÊt tho¶ m·n: x - y = 1
d) T×m a ®Ó hÖ ph­¬ng tr×nh cã nghiÖm duy nhÊt tho¶ m·n x vµ y lµ c¸c sè nguyªn.
Bµi tËp 14: a) Gi¶i vµ biÖn luËn hÖ ph­¬ng tr×nh: (I)
b) Trong tr­êng hîp hÖ ph­¬ng tr×nh (I) cã nghiÖm duy nhÊt h·y t×m m ®Ó x+y lín h¬n 1
Bµi tËp 15: X¸c ®Þnh a, b ®Ó hpt: a. Cã nghiÖm lµ b. Cã VSN.
Chuùc caùc em hoïc toát!
Mét sè bµi tËp: ph­¬ng tr×nh bËc hai
ph­¬ng tr×nh quy vÒ ph­¬ng tr×nh bËc hai.
Bµi tËp 1: Cho ph­¬ng tr×nh: x2 - 2(3m + 2)x + 2m2 - 3m + 5 = 0
a) Gi¶i ph­¬ng tr×nh víi m lÇn l­ît b»ng c¸c gi¸ trÞ:
m = 2; 	m = - 2; 	m = 5; 	m = -5;	 m = 3; 	m = 7; m = - 4
b) T×m c¸c gi¸ trÞ cña m ®Ó ph­¬ng tr×nh cã mét nghiÖm x lÇn l­ît b»ng
x = 3; 	x = -3; 	x = 2; 	x = 5; 	x = 6; 	x = -1
c) T×m c¸c gi¸ trÞ cña m ®Ó ph­¬ng tr×nh trªn cã nghiÖm kÐp.
Bµi tËp 2: Cho ph­¬ng tr×nh: x2 - 2(m + 3)x + m2 + 3 = 0
a) Gi¶i ph­¬ng tr×nh víi m = -1vµ m = 3
b) T×m m ®Ó ph­¬ng tr×nh cã mét nghiÖm x = 4
c) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm ph©n biÖt; Cã hai nghiÖm tho· m·n ®iÒu kiÖn x1 = x2
Bµi tËp 3: Cho ph­¬ng tr×nh : ( m + 1) x2 + 4mx + 4m - 1 = 0
a) Gi¶i ph­¬ng tr×nh víi m = -2 
b) Víi gi¸ trÞ nµo cña m th× ph­¬ng tr×nh cã hai nghiÖm ph©n biÖt
c) Víi gi¸ trÞ nµo cña m th× ph­¬ng tr×nh ®· cho v« nghiÖm; Cã hai nghiÖm tho· m·n x1 = 2x2 
Bµi tËp 4: Cho ph­¬ng tr×nh : 2x2 - 6x + (m +7) = 0
a) Gi¶i ph­¬ng tr×nh víi m = -3 
b) Víi gi¸ trÞ nµo cña m th× ph­¬ng tr×nh cã mét nghiÖm x = - 4
c) Víi gi¸ trÞ nµo cña m th× pt cã hai nghiÖm ph©n biÖt; ph­¬ng tr×nh ®· cho v« nghiÖm
d) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm tho· m·n ®iÒu kiÖn x1 = - 2x2
Bµi tËp 5: BiÕt r»ng ph­¬ng tr×nh : x2 - (6m + 1 )x - 3m2 + 7 m - 2 = 0 (Víi m lµ tham sè ) cã mét nghiÖm x = 1. T×m nghiÖm cßn l¹i
Bµi tËp 6:	BiÕt r»ng ph­¬ng tr×nh : x2 - 2(m + 1 )x + m2 - 3m + 3 = 0 ( Víi m lµ tham sè ) cã mét nghiÖm x = -1. T×m nghiÖm cßn l¹i.
Bµi tËp 7: Cho ph­¬ng tr×nh: x2 - mx + 2m - 3 = 0 
a) Gi¶i ph­¬ng tr×nh víi m = - 5
b) T×m m ®Ó ph­¬ng tr×nh cã nghiÖm kÐp; Cã hai nghiÖm ph©n biÖt
c) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm tr¸i dÊu
d)T×m hÖ thøc gi÷a hai nghiÖm cña ph­¬ng tr×nh kh«ng phô thuéc vµo m 
Bµi tËp 8: Cho ph­¬ng tr×nh bËc hai (m - 2)x2 - 2(m + 2)x + 2(m - 1) = 0
a) Gi¶i ph­¬ng tr×nh víi m = 3
b) T×m m ®Ó ph­¬ng tr×nh cã mét nghiÖm x = - 2
c) T×m m ®Ó ph­¬ng tr×nh cã nghiÖm kÐp; Cã hai nghiÖm ph©n biÖt
d) T×m hÖ thøc liªn hÖ gi÷a hai nghiÖm kh«ng phô thuéc vµo m
e) Khi ph­¬ng tr×nh cã mét nghiÖm x = -1 t×m gi¸ trÞ cña m vµ t×m nghiÖm cßn l¹i
Bµi tËp 9:Cho ph­¬ng tr×nh: x2 - 2(m- 1)x + m2 - 3m = 0 
a) Gi¶i ph­¬ng tr×nh víi m = - 2
b) T×m m ®Ó ph­¬ng tr×nh cã mét nghiÖm x = - 2. T×m nghiÖm cßn l¹i
c) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm ph©n biÖt
d) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm x1 vµ x2 th¶o m·n: x12 + x22 = 8
e) T×m gi¸ trÞ nhá nhÊt cña A = x12 + x22 
Bµi tËp 10: Cho ph­¬ng tr×nh: mx2 - (m + 3)x + 2m + 1 = 0 
a) T×m m ®Ó ph­¬ng tr×nh cã nghiÖm kÐp; cã hai nghiÖm ph©n biÖt
c) T×m m ®Ó ph­¬ng tr×nh cã hiÖu hai nghiÖm b»ng 2
d) T×m hÖ thøc liªn hÖ gi÷a x1vµ x2 kh«ng phô thuéc m 
Bµi tËp 11: Cho ph­¬ng tr×nh: x2 - (2a- 1)x - 4a - 3 = 0 
a) Chøng minh r»ng ph­¬ng tr×nh lu«n cã nghiÖm víi mäi gi¸ trÞ cña a
b) T×m hÖ thøc liªn hÖ gi÷a hai nghiÖm kh«ng phô thuéc vµo a
c) T×m gi¸ trÞ nhá nhËt cña biÓu thøc A = x12 + x22 
Bµi tËp 12: Cho ph­¬ng tr×nh: x2 - (2m- 6)x + m -13 = 0
a) Chøng minh r»ng ph­¬ng tr×nh lu«n cã hai nghiÖm ph©n biÖt
b) T×m gi¸ trÞ nhá nhÊt cña biÓu thøc A = x1. x2 - x12 - x22 
Bµi tËp 13: Cho ph­¬ng tr×nh: x2 - 2(m+4)x + m2 - 8 = 0
a) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm ph©n biÖt
b) T×m m ®Ó A = x12 + x22 - x1 - x2 ®¹t gi¸ trÞ nhá nhÊt
c) T×m m ®Ó B = x1 + x2 - 3x1x2 ®¹t gi¸ trÞ lín nhÊt
d) T×m m ®Ó C = x12 + x22 - x1x2
Bµi tËp 14: Cho ph­¬ng tr×nh: ( m - 1) x2 + 2mx + m + 1 = 0
a) Gi¶i ph­¬ng tr×nh víi m = 4
b) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm tr¸i dÊu
c) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm x1 vµ x2 tho¶ m·n: A = x12 x2 + x22x1
d) T×m hÖ thøc liªn hÖ gi÷a hai nghiÖm kh«ng phô thuéc vµo m 
Bµi tËp 15:Cho ph­¬ng tr×nh x2 - 2(m - 2)x + (m2 + 2m - 3) = 0. 
T×m m ®Ó ph­¬ng tr×nh cã 2 nghiÖm x1, x2 ph©n biÖt tho¶ m·n 
Bµi tËp 16: Cho ph­¬ng tr×nh: mx2 - 2(m + 1)x + (m - 4) = 0 (m lµ tham sè).
a) X¸c ®Þnh m ®Ó c¸c nghiÖm x1; x2 cña ph­¬ng tr×nh tho¶ m·n x1 + 4x2 = 3
b) T×m mét hÖ thøc gi÷a x1; x2 mµ kh«ng phô thuéc vµo m
Bµi tËp 17: Cho ph­¬ng tr×nh mx2 - 2(m + 1)x + (m - 4) = 0
a) T×m m ®Ó ph­¬ng tr×nh cã nghiÖm.
b) T×m m ®Ó ph­¬ng tr×nh cã 2 nghiÖm tr¸i dÊu. Khi ®ã trong hai nghiÖm, nghiÖm nµo cã gi¸ trÞ tuyÖt ®èi lín h¬n?
c) X¸c ®Þnh m ®Ó c¸c nghiÖm x1; x2 cña ph­¬ng tr×nh tho¶ m·n: x1 + 4x2 = 3.
d) T×m mét hÖ thøc gi÷a x1, x2 mµ kh«ng phô thuéc vµo m.
Bµi tËp 18: Gäi x1; x2 lµ nghiÖm cña ph­¬ng tr×nh:	2x2 + 2(m + 1)x + m2 + 4m + 3 = 0
T×m gi¸ trÞ lín nhÊt cña biÓu thøc: A =½x1x2 - 2x1 - 2x2½
Bµi tËp 19: a) Víi gi¸ trÞ nµo m th× hai pt sau cã Ýt nhÊt 1 nghiÖm chung. T×m nghiÖm chung ®ã x2 - (m + 4)x + m + 5 = 0	(1) x2 - (m + 2)x + m + 1 = 0	(2)
b) T×m gi¸ trÞ cña m ®Ó nghiÖm cña pt (1) lµ nghiÖm cña ph­¬ng tr×nh (2) vµ ng­îc l¹i.
Bµi tËp 20:	Gäi x1, x2 lµ c¸c nghiÖm cña ph­¬ng tr×nh: x2 - (2m - 1)x + m – 2 = 0
T×m m ®Ó cã gi¸ trÞ nhá nhÊt
Bµi tËp 21: Gäi x1, x2 lµ c¸c nghiÖm cña ph­¬ng tr×nh.
x2 + 2(m - 2)x - 2m + 7 = 0
T×m m ®Ó cã gi¸ trÞ nhá nhÊt.
Bµi tËp 22: Cho ph­¬ng tr×nh: x2 - m + (m - 2)2 = 0
T×m gi¸ trÞ lín nhÊt vµ nhá nhÊt cña biÓu thøc A = x1x2 + 2x1 + 2x2
Bµi tËp 23: Cho ph­¬ng tr×nh: x2 - 2(m + 1)x + 2m + 10 = 0 (m lµ tham sè). T×m m sao cho 2 nghiÖm x1; x2 cña ph­¬ng tr×nh tho¶ m·n 10x1x2 + ®¹t gi¸ trÞ nhá nhÊt. T×m gi¸ trÞ ®ã.
Bµi tËp 24: Cho ph­¬ng tr×nh : x2 - 2(m - 1 ) x + m + 1 = 0
a) Gi¶i ph­¬ng tr×nh víi m = 4 
b) Víi gi¸ trÞ nµo cña m th× ph­¬ng tr×nh cã hai nghiÖm ph©n biÖt
c) Víi gi¸ trÞ nµo cña m th× ph­¬ng tr×nh ®· cho v« nghiÖm
d) T×m m ®Ó ph­¬ng tr×nh cã hai nghiÖm tho· m·n ®iÒu kiÖn x1 = 3x2 
Bµi tËp 25: Cho ph­¬ng tr×nh x2 - (m + 3)x + 2(m + 1) = 0 	(1)
T×m gi¸ trÞ cña tham sè m ®Ó ph­¬ng tr×nh cã (1) cã nghiÖm x1 = 2x2.
Chuùc caùc em hoïc toát!
Mét sè bµi tËp: gi¶i bµi to¸n b»ng c¸ch lËp ph­¬ng tr×nh
HÖ ph­¬ng tr×nh.
1/ Gi¶i bµi to¸n b»ng c¸ch lËp HPT
BÀI TOÁN VỀ SỐ - CHỮ SỐ
Tìm 2 số tự nhiên biết tổng của chúng bằng 1006 và nếu lấy số lớn chia số nhỏ thì được thương là 2 và dư là 124. 
( KQ:712 và 294 )
Tìm 2 số biết tổng của chúng bằng 212, nếu lấy số lớn chia số nhỏ thì được thương là 5 và dư 8.
( KQ: 178 và 34) 
Tìm hai số tổng bằng hiệu bình phương của chúng và bằng 23. 
( KQ: 12 và 11 )
Tìm số có hai chữ số biết chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 và số đó gấp 7 lần tổng các chữ số của nó. 
 ( KQ: 42)
Tìm số tự nhiên có hai chữ số, tổng các chữ số bằng 10,nếu đổi vị trí hai chữ số cho nhau thì số đó giảm đi 54 đơn vị.
HD: Gọi x; y là chữ số hàng chục và hàng đơn vị( x ; y N và ) 
Ta có hệ: ( KQ: 82)
Tìm số tự nhiên có hai chữ số , chữ số hàng cghucj lớn hơn chữ số hàng đơn vị là 2 và nếu viết số 0 vào giữa hai chữ số thì số đó tăng thêm 540 đơn vị.
HD: Gọi x; y là chữ số hàng chục và hàng đơn vị( x ; y N và )
.ta có số 
Ta có hệ: ( KQ: 64)
Tìm 1 số có hai chữ số,biết rằng số đó chia cho tổng hai chữ số của nó thì được thương là 8 không dư.Còn nếu chia số đó cho số viết theo thứ tự ngược lại thì được thương là 2 và dư 18.
HD: Gọi x; y là chữ số hàng chục và hàng đơn vị( x ; y N và ) 
Ta có hệ: ( KQ: 72)
T×m mét sè cã hai ch÷ sè, biÕt r»ng sè ®ã gÊp 7 lÇn ch÷ sè hµng ®¬n vÞ cña nã vµ nÕu sè cÇn t×m chia cho tæng c¸c ch÷ sè cña nã th× ®­îc th­¬ng lµ 4 vµ sè d­ lµ 3.
NÕu tö sè cña mét ph©n sè ®­îc t¨ng gÊp ®«i vµ mÉu sè thªm 8 th× gi¸ trÞ cña ph©n sè b»ng . NÕu tö sè thªm 7 vµ mÉu sè t¨ng gÊp 3 th× gi¸ trÞ ph©n sè b»ng . T×m ph©n sè ®ã.
BÀI TOÁN CÓ NỘI DUNG HÌNH HỌC
Tính độ dài hai cạnh góc vuông của một tam giác vuông,biết nếu tăng mỗi cạnh lên 3cm thì diện tích tam giác tăng 36 cm2 ,và nếu một cạnh giảm đi 4cm thì diện tích tam giác giảm đi 26cm2. 
Một hình chữ nhật có chiều dài hơn chiều rộng 20 cm diện tích là 300 cm2. Tính chiều dài , rộng của hình chữ nhật đó.( KQ: 30cm và 10 cm)
Tính các kích của hình chữ nhật biết chiều dài hơn rộng 5cm,chu vi = 70cm. 
( KQ: 20cm và 15 cm)
Tính chu vi của hình chữ nhật biết nếu tăng mỗi cạnh của nó lên 1cm thì diện tích tăng lên 22cm2. Nếu giảm chiều dài đi 2cm chiều rộng 1cm thì diện tích giảm 28cm2. ( KQ: 42cm )
Mét khu v­ên h×nh ch÷ nhËt cã chu vi lµ 280 m. Ng­êi ta lµm lèi ®i xung quanh v­ên (thuéc ®Êt trong v­ên) réng 2 m. TÝnh kÝch th­íc cña v­ên, biÕt r»ng ®Êt cßn l¹i trong v­ên ®Ó trång trät lµ 4256 m2.
BÀI TOÁN CHUYỂN ĐỘNG
Một ôtô đi quãng đường AB hết 8giờ.Lúc đầu ôtô đi với vận tốc 40 km/h sau đó đi với vận tốc 60 km/h. Tính thời gian ôtô đi với mỗi vân tốc trên,biết rằng nếu ôtô đi với vận tốc 45 km/h thì trong 8giờ ôtô đi hết quãng đường AB.
 ( KQ:6h ; 4h )
Hai xe cùng khởi hành từ A và B và đi ngược chiều nhau.Sau khi đi được 2 giờ thì họ gặp nhau cách chính giữa quãng đường AB là 15 km.Nếu vận tốc xe chạy nhanh hơn giảm đi một nửa vận tốc ban đầu thì hai xe gặp nhau sau khi khởi hành 2giờ 48phút. Tính vận tốc ban đầu của mỗi xe. 
 (KQ: 60km/h và 45km/h )
Một ôtô dự định đi từ A đến B trong thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10 km thì sẽ đến sớm hơn 3h, nếu xe đi chậm mỗi giờ 10 km thì đến muộn mất 5h. Tính thời gian dự định, vận tốc của xe lúc đầu và quãng đường AB. ( ĐK: x ; y > 0 ) ( KQ: 15h; 40 km/h v à 600km )
Quãng đườngAB gồm một đoạn lên dốc dài 4km, một đoạn xuống dốc dài 5km.Một người đi xe đạp từ A dến b hết 40 phút và đi từ B về A hết 41 phút ( vận tốc khi lên mỗi như nhau và xuống mỗi dốc như nhau ). Tính vận tốc lúc lên và xuống dốc. ( KQ: 12 km/h và 15 km/h )
Một người đi xe máy từ A đến B với vận tốc 30 km/h nhưng đến C thì đường xấu nên từ đó người ấy chỉ đi với vận tốc 20 km/h.Tính quãng đường AC và AB biết tổng thời gian người ấy đi hết quãng đường AB là 4h 20 phút và quãng đường CB dài hơn quãng đường AC là 20 km.
HD: Đặt AC = x km. CB = y km
Ta có hệ: ( KQ: AC = 40 km; CB = 60 km )
BÀI TOÁN CHUYỂN ĐỘNG DƯỚI NƯỚC
Một chiếc thuyền đi từ bến A Sau 48 phút 1 chiếc tàu thủy cũng đi từ A và đuổi theo gặp thuyền cách bến A 30 km.Tính vận tốc của thuyền máy và tàu thủy biết tàu thủy chạy nhanh hơn thuyền máy là 10 km/h.
HD: Gọi x ;y là vận tốc chiếc thuyền và tàu thủy ( x ;y > 0)
Ta có hệ: ( KQ: 15 km/h ; 25 km/h )
* Hai bến sông A và B cách nhau 40 km.Một ca nô xuôi từ A đến B rồi lại quay về A với vận tốc riêng không đổi hết tất cả 2 giờ 15 phút.Khi ca nô khởi hành từ A thì cùng lúc đó ,một khúc gỗ cũng trôi tự do từ A theo dòng nước và gặp ca nô trên đường trở về tại một điểm cách A là 8 km.Tính vận tốc của ca nô và dòng nước.
HD: Gọi x ; y là vận tốc của ca nô và dòng nước( x > y > 0 )
Vận tốc ca nô xuôi và ngược dòng là: x + y km/h và x – y km/h.
Cả đi và về hết 2giờ15phút Hay 9/4 giờ. Ta có PT: 
Thời gian ca nô xuôi và ngược: (h). Thời gian khúc gỗ trôi 8km: ....
Ta có : (KQ:36 và4 km/h)
BÀI TOÁN “ CHUNG – RIÊNG ”
Hai vòi nước cùng chảy vào một cái bể cạn nước trong 6h thì đầy bể.Nếu mở vòi I trong 2h và vòi II trong 3h thì được 2/5 bể. Tính thời gian mỗi vòi chảy một mình đầy bể. ( KQ: 10h và 15h )
Hai vòi nước cùng chảy vào một cái bể trong 1h20 phút thì đầy bể.Nếu mở vòi I trong 10 phút và vòi II trong 12 phút thì được 2/15 bể. Tính thời gian mỗi vòi chảy một mình đầy bể. ( KQ: 2h và 4h )
Hai vòi nước cùng chảy trong 4h 48phút thì đầy bể.Nếu vòi I chảy trong 4h và vòi II trong 6h thì sẽ đầy bể.Hỏi nmỗi vòi chảy một mình trong bao lâu thì đầy bể. ( KQ: 8h và 12h ) 
Hai người cùng xây 1 bức tường.Người thứ nhất làm được một nửa rồi để cho người thứ hai làm nốt cho đến lúc xong thì hết 8 giờ.Nếu cả hai người làm chung thì chỉ sau 3 giờ thì xong bức tường.Hỏi nếu làm một mình thì mỗi người phải mất bao lâu mới xong.
HD: Gọi x ; y là thời gian người thứ I và II làm một mình xong công việc.
Ta có hệ: ( KQ : 12 giờ và 4 giờ ) 
Nếu hai tổ HS cùng vệ sinh sân trường thì sau 1giờ 30 phút sẽ xong.Nếu để tổ I làm trong 20 phút,tổ II làm trong 15 phút thì được 1/5 sân trường.Hỏi mỗi tổ làm riêng thì xong trong bao lâu. ( KQ:2,5h và 3,75h )
BÀI TOÁN VỀ TUỔI
Hai năm trước tuổi của người Anh gấp 3 lần tuổi của người em. Hai năm sau tuổi của người Anh gấp 2 lần tuổi của người em.Tính tuổi của người Anh và người Em hiện nay. 
 HD: Gọi x; y là tuổi anh và tuổi em hiện nay ( x ; y nguyên dương)
Ta có hệ: ( KQ: 14 tuổi và 6 tuổi )
* Tuổi của hai anh em cộng lại bằng 21.Tuổi anh hiện nay gấp đôi tuổi em lúc anh bằng tuổi em hiện nay.Tính tuổi hiện nay của mỗi người.
HD: Gọi tuổi của anh và em hiện nay là x và y. Ta có PT x +y =21
 Tuổi anh hiện nay gấp đôi tuổi em trước kia nên tuổi em trước kia bằng x/2. 
Tuổi anh trước kia bằng tuổi em hiện nay nên tuổi anh trước kia bằng y.Do hiệu số tuổi 2 người không đổi theo thời gian nên ta có PT: x – y = 
 Ta có hệ: ( KQ : 12 tuổi và 9 tuổi )
BÀI TOÁN CÓ NỘI DUNG HOÁ – LÍ
Có hai lọ đựng muối với nồng độ muối là 5% và 40% . Hỏi cần phải lấy mỗi loại bao nhiêu gam để được 140g muối có nồng độ 30%.
HD: Gọi x(g); y(g)lần lượt là khối lượng nước muối lấy ở hai lọ (x; y > 0 )
 Ta có hệ: (KQ: 40g ; 100g )
BÀI TOÁN VỀ TỈ SỐ
Theo kế hoạch,trong quý I xưởng A phải sản xuất nhiều hơn xưởng B lµ 200 sản phẩm.Nhưng do thực hiện xưởng A tăng n