Chuyên đề ôn thi THPT Quốc gia môn Vật lý - Chuyên đề: Đồ thị dao động cơ của các hàm điều hòa

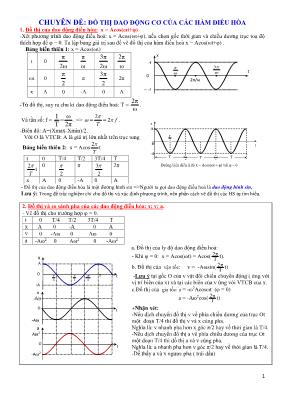
1 
CHUYÊN ĐỀ: ĐỒ THỊ DAO ĐỘNG CƠ CỦA CÁC HÀM ĐIỀU HÒA 
1. Đồ thị của dao động điều hòa: x = Acos(ωt+φ) 
-Xét phương trình dao động điều hoà: x = Acos(ωt+φ), nếu chọn gốc thời gian và chiều dương trục toạ độ 
thích hợp để φ = 0. Ta lập bảng giá trị sau để vẽ đồ thị của hàm điều hoà x = Acos(ωt+φ) . 
 Bảng biến thiên 1: x = Acos(ωt) 
t 0 
π
2ω
π
ω
3π
2ω
2π
ω
ωt 0 
π
2
 π 
3π
2
 2π 
x A 0 -A 0 A 
-Từ đồ thị, suy ra chu kì dao động điều hoà: T = 
2π
ω
. 
 Và tần số: f = 
1 ω
=
T 2π
. => 
2
2 f
T

   . 
-Biên độ: A=(Xmax-Xmin)/2. 
 Với O là VTCB: A là giá trị lớn nhất trên trục tung 
 Bảng biến thiên 2: x = Acos
2
T

t 
t 0 T/4 T/2 3T/4 T 
2
T

t 
0 
2

π 3
2

2π 
x A 0 -A 0 A 
 - Đồ thị của dao động điều hòa là một đường hình sin =>Người ta gọi dao động điều hoà là dao động hình sin. 
 Lưu ý: Trong đề trắc nghiệm chỉ cho đồ thị và xác định phương trình, nên phần cách vẽ đồ thị các HS tự tìm hiểu. 
2. Đồ thị và so sánh pha của các dao động điều hòa: x; v; a. 
- Vẽ đồ thị cho trường hợp  = 0. 
t 0 T/4 T/2 3T/4 T 
x A 0 -A 0 A 
v 0 -A 0 A 0 
a -A2 0 A2 0 -A2 A2 
 a. Đồ thị của ly độ dao động điều hoà: 
- Khi  = 0: x = Acos(t) = Acos( 2π
T
t). 
b. Đồ thị của vận tốc: v = -Asin( 2π
T
t) 
 -Lưu ý tại gốc O của v vật đổi chiều chuyển động ( ứng với 
vị trí biên của x) và tại các biên của v ứng với VTCB của x. 
c.Đồ thị của gia tốc: a = -ω2Acost ( = 0) 
 a = -A2cos( 2π
T
t) 
+Nhận xét: 
-Nếu dịch chuyển đồ thị v về phía chiều dương của trục Ot 
một đoạn T/4 thì đồ thị v và x cùng pha. 
Nghĩa là: v nhanh pha hơn x góc π/2 hay về thời gian là T/4. 
-Nếu dịch chuyển đồ thị a về phía chiều dương của trục Ot 
một đoạn T/4 thì đồ thị a và v cùng pha. 
Nghĩa là: a nhanh pha hơn v góc π/2 hay về thời gian là T/4. 
-Dễ thấy a và x ngược pha ( trái dấu) 
x 
v 
 a 
 t 
 t 
 t T 
2
T 
4
T 
4
3T 
O 
O 
O 
 A 
-A 
A 
 -A 
 -A2 
 A2 
O t 
x 
A 
-A 
T T T 
T
2 
Đường biểu diễn li độ x = Acos(ωt + φ) với φ = 0 
A
t 
0 
x 
A


2π/ω 
3

2 
3. Đồ thị của ly độ ,vận tốc và gia tốc dao động điều hoà vẽ chung trên 1 hệ tọa độ: 
 a. Ly độ: x = Acos(ωt+φ), 
 b. Vận tốc: v = x/ = -Aωsin(ωt+φ) = Aωcos(ωt+φ +
π
2
). 
 |v|max = Aω khi sin(ωt+φ) = 1. 
=> Tốc độ của vật dao động điều hoà đạt giá trị cực đại khi vật qua vị trí cân bằng. 
 c. Gia tốc: a = v/ = [-Aωsin(ωt+φ)]/ = -Aω2cos(ωt+φ) = -ω2x.  a = -Aω2cos(ωt+φ) = -ω2x 
 |a|max = Aω2 khi cos(ωt+φ) = -1. 
 =>Gia tốc của vật dao động điều hoà có độ lớn đạt giá trị cực đại khi khi vật ở biên( |x| = A). 
t 
x, v, a 
A 
-A 
ωA 
-ωA 
ω2A 
-ω2A 
O T T/2 
T 
Đường biểu diễn x(t), v(t) và a(t) vẽ trong cùng một 
hệ trục toạ độ, ứng với φ = 0 
a(t) 
v(t) 
x(t) 
4: Đồ thị năng lượng trong dao động điều hoà 
a. Sự bảo toàn cơ năng: 
Dao động của con lắc đơn, và con lắc lò xo dưới tác dụng của lực thế ( trọng lực và lực đàn hồi ...) và không có 
ma sát nên cơ năng của nó được bảo toàn. Vậy cơ năng của vật dao động được bảo toàn. 
b. Biểu thức thế năng: 
 Xét con lắc lò xo. Tại thời điểm t bất kì vật có li độ 
 x= Acos(t+) và lò xo có thế năng: 
 Wt=
1
2
kx2 =
1
2
kA2cos2(t+) 
 Thay k = 2m ta được:Wt=
1
2
m2A2cos2(t+) 
 Đồ thị Wt ứng với trường hợp  = 0 ở hình bên. 
c. Biểu thức động năng: 
  Tại thời điểm t bất kì vật nặng m có vận tốc 
 v = -Asin(t+) và có động năng 
 Wđ =
1
2
mv2 =
1
2
mA22sin2(t+) 
  Đồ thị Wđ ứng với trường hợp  = 0 ở hình bên. 
d. Biểu thức cơ năng: 
  Cơ năng của vật tại thời điểm t: 
 W = Wt + Wđ 
 = 
1
2
m2A2cos2(t+) + 
1
2
mA22sin2(t+) 
 = 
1
2
m2A2[cos2(t+) + sin2(t+)] 
 W = 
1
2
m2A2 = const. 
  Đồ thị Wt, Wđ vẽ trong cùng một hệ trục toạ độ ở hình bên. 
Wt 
t 
2
T 
4
T O 
1
4 m
2
A
2
1
2 m
2
A
2
t O 
m  2 A 2 
m  2 A 2 
T/2 T/4 
1/2 
Wd 
1/4 
Wt 
t 
2
T
4
TO 
1
4 m
2
A
2
1
2 m
2
A
2
Wđ 
W 
3 
5. Phương pháp xác định phương trình từ đồ thị: 
a. Xác định biên độ: Nếu tại VTCB x=0 thì: 
 x = xmax = A (Từ số liệu trên đồ thị ta có thể xác định A ). 
 v = vmax =ωA (Từ số liệu trên đồ thị ta có thể xác định vmax ). 
 a = amax = ω2A (Từ số liệu trên đồ thị ta có thể xác định amax ). 
b. Xác định pha ban đầu : 
-Nếu là hàm cos, dùng công thức : 0
x
cos
A
  ; 0v
max
v
cos
v
  ; 0a
max
a
cos
a
  
Lưu ý: Lúc t = 0 đồ thị cắt trục tung tại x0 ( x = x0 : Có 9 vị trí đặc biệt của x0 ; mỗi x0 có 2 giá trị đặc biệt 
của  tương ứng trái dấu , dấu của  ngược dấu với vận tốc v; riêng các vị trí đặc biệt: x0= A=> = 0; x0= -
A=> = π . Vậy có 16 giá trị đặc biệt của ) . Xem hình sau: 
Lược đồ pha ban đầu  theo các vị trí đặc biệt x0 
0 
-A • • • • • • • • • 
O A 2
A
 2
A 
2
A
 
2
3A
 
2
A
2
3A 
x 
6
 
4
 
3
 2
 
3
2 
4
3
6
5 
6

 
4

 
3

 
2

 3
2
 
4
3
 
6
5
 
B- C3/2
- HD- NB- VTCB NB
+ HD+ C3/2+ B+ 
 
V<0 
V>0 
 x A 0 A
3
2
A 3
2
A2
2
A
2
A 2
2
A
2
A
24
T
12
T
24
T
24
T
24
T
12
T
12
T
12
T
 x 
Vận tốc: 
0 0 max
2
v
max 3
2
v
max
2
v
max 3
2
v
max
2
v
max
2
v
O 
 x 
-ω2A 
0 2A 
max 3
2
a max 3
2
a
max 2
2
a max
2
a max 2
2
a
max
2
a
24
T
12
T
24
T
24
T
24
T
12
T
12
T
12
T
Gia tốc: 
4 
c. Xác định chu kì T ( Suy ra tần số f hoặc tần số góc ): 
Nhận dạng thời điểm trạng thái lặp lại, hay chu kì T là khoảng thời gian giữa hai điểm cùng pha gần nhất . Rồi suy 
ra tần số f (hoặc tần số góc  ) 
- Dựa vào thời gian ghi trên đồ thị và pha ban đầu, vẽ lại đường tròn Fresnel để xác định góc quét tương ứng với thời 
gian sau đó áp dụng công thức tìm : 
t





 Lưu ý: 
- Các đồ thị dao động điều hòa của li độ (x), vận tốc (v) và gia tốc (a) biến thiên điều hòa theo hàm số sin hoặc 
cos với chu kì T. 
- Các đồ thị động năng và thế năng biến thiên tuần hoàn theo hàm số sin hoặc cos với chu kì T/2 
⋇ Vận dụng giải các bài tập về đồ thị, chúng ta quan sát đồ thị tìm ra các đại lượng dựa quy luật sau: 
 + Tìm biên độ dao động dựa vào trục giới hạn cắt điểm nào đó trên trục tung (tìm biên độ A, Aω hoặc Aω2). 
 + Tìm chu kì dao động dựa vào sự lặp lại trên trục thời gian, hoặc dựa vào khoảng thời gian gần nhất cùng pha để 
vật nhận giá trị nào đó. 
 + Tại thời điểm t thì x = ?, v = ? , a = ? sẽ tìm được pha ban đầu φ và chu kì T. Suy ra tần số góc ω. 
 + Dựa vào đường tròn và vận dụng các công thức của dao động tìm các đại lượng và các yếu tố cần tìm. 
-Các đồ thị của ly độ x theo thời gian t sau đây cho biết một số giá trị của x0 và  lúc t = 0: 
-Xác định chu kì T, rồi suy ra tần số f (hoặc tần số góc ): Thường căn cứ vào số liệu trên trục thời gian. 
 (Mô hình mối liên hệ giá trị của các đại lượng x,v,a,F tại các vị trí đặc biệt: x=0; x =-A;x =A ) 
A
t 
0 
x 
A
2
T
T 
4
T 3
4
T
t= 0; X0= A; =0 
A
t 
0 
x 
A
2
T
T 
4
T
3
4
T
t= 0; X0= 0; v0 > 0; =-π/2 
A
t 
0 
x 
A
2
T
T 
4
T
3
4
T
t= 0; X0= 0; v0 < 0; =π/2 
A
t 
0 
x 
A
2
T
T 
4
T 3
4
T
t= 0; X0= -A; =π; -π 
A
t 
0 
x 
A
12
T
7
12
T
t=0;
0
3
2
A
x  ; = -π/6 
13
12
T
3
2
A
A
t 
0 
x 
A
8
T
5
8
T
t=0;
0
2
2
A
x  ; = -π/4 
9
8
T
2
2
A
A
t 
0 
x 
A
6
T
2
3
T
t=0;
0
2
A
x  ; = -π/3 
7
6
T
2
A
x 
A
t 
0 
A
2
A

T/3 
12
T
5
6
T
t= 0; x0= -A/2; v0 > 0; = - 2π/3 
4
3
T
A
t 
0 
A
2
2
A

3T/8 
8
T
7
8
T
t= 0; x0= - 2
2
A ; v0 > 0; = - 3π/4 
11
8
T
5 
6: Các ví dụ: 
Ví dụ 1: Vật dao động điều hòa có đồ thị tọa độ như hình bên. Phương trình dao động là: 
A. x = 2cos (5t + ) cm. 
B. x = 2cos (5t -
2
π
) cm. 
C. x = 2cos 5t cm. 
D. x = 2cos (5t +
2
π
) cm. 
Hướng dẫn giải : 
Theo đồ thị ta có chu kì T = 0,4 s, A = 2 cm; 
Khi t = 0, x = 0, v < 0 (t tăng có x giảm)   =
2
π
;  = 
T
2π
 = 
0,4
2π
 = 5 rad/s. Đáp án D. 
Ví dụ 2: Đồ thị li độ của một vật dao động điều hoà có dạng như hình vẽ. Phương trình dao động của vật là: 
A. 4 os ( )
3 3
x c t cm
 
  
B. 4 os ( 1)
3
x c t cm

  
C. 4 os(2 )
6
x c t cm

  
D. 
2
4 os( )
7 6
x c t cm
 
  
Hướng dẫn giải : 
Trên đồ thị cho ta: A= 4cm ; Khi t=0 thì x0 = 2 => cos = x0/A = 2/4 = 0,5 => = -π/3 ( Do x đang tăng ) 
Theo đồ thị : Vật từ x0 =2cm=A/2 đến x= 4cm=A , mất thời gian ngắn nhất là T/6 ( xem sơ đồ giải nhanh) 
=> Chu kỳ T = 7- T/6 => T= 6s => ω = 2π/T = π/3 rad/s => 4
3 3
x cos( t )cm
 
  . Đáp án B. 
Ví dụ 3: Một chất điểm dao động điều hoà dọc theo trục Ox, với O trùng với vị trí cân bằng của chất điểm. Đường 
biểu diễn sự phụ thuộc li độ x chất điểm theo thời gian t cho ở hình vẽ. Phương trình vận tốc của chất điểm là 
A. 60 10
3
v cos( t )( cm / s )

   
B. 60 10
6
v cos( t )( cm / s )

   
C. 60 10
3
v cos( t )( cm / s )

  
D. 60 10
6
v cos( t )( cm / s )

  
Hướng dẫn giải: 
-Từ đồ thị ta có biên độ của x: A = 6cm. 
-Lúc đầu t= 0 thì x0 = -3 cm = -A /2 và vật đang đi theo chiều dương nên pha ban đầu: -2π/3. 
-Từ đồ thị ta có chu kì: T= 0,2s =>
2 2
10
0 2
rad / s
T ,
 
    .=> 
2
6 10
3
x cos( t )( cm )

  . 
-Biên độ vận tốc : vmax =ωA = 10π.6 =60π cm/s 
-Vận tốc nhanh pha hơn li độ một góc π/2 nên ta có : 
2
60 10 60 10
3 2 6
v cos( t ) cos( t )( cm / s )
  
        .Đáp án B. 
t(s) 
0,4 0,2 
x(cm) 
6 
3 
-3 
-6 
O 
0 
– 2 
2 
x(cm) 
t(s) 
0,2 
0,4 
0,6 
0,8 
4
t(s) 
0 
x(cm) 
4
Hình ví dụ 2 
7
2
6 
Ví dụ 4: Một vật dao động điều hoà có độ thi vận tốc - thời gian như hình vẽ. Phương trình dao động của vật là 
A. x = 1,2
25 5
os( )( )
3 6
c t cm
 
B. x= 1,2
25
os( )( )
3 6
c t cm
 
C. x= 2,4cos
10
( )( )
3 3
t cm
 
 
D.x= 2,4cos(
10
)( )
3 2
t cm
 
 
Hướng dẫn giải: 
 Sơ đồ liên hệ các đại lượng x, v trong dao động điều hòa: 
-Xác định pha ban đầu: 
Theo đồ thị ta có: vmax =10π cm/s; v0 = 5π cm/s= vmax/2 và vận tốc đang tăng nên phương trình vận tốc: 
 v= 10πcos(ωt-π/3) cm/s . 
+Do pha của x chậm hơn pha của v một góc π/2 nên pha ban đầu của ly độ x là: = -π/2 –π/3=-5π/6 
+Cách khác: Theo đồ thị và kết hợp với sơ đồ liên hệ giữa x và v ta thấy: 
Vận tốc lúc đầu v0 = vmax/2 và tăng dần, nghĩa là vật từ vị trí 0
3
2
A
x   theo chiều dương. 
Suy ra pha ban đầu của ly độ x là:  = -5π/6 
-Xác định chu kì, tần số góc: Khoảng thời gian ngắn nhất từ 
0
3
2
A
x   đến VTCB( x = 0 ) là T/6. 
Theo đồ thị ta có: T/6 +T/4 =0,1s =>T =0,24s => Tần số: 
2 2 25
0 24 3
rad / s
T ,
  
    
-Xác định biên độ của x: 
10
1 2
25
3
maxvA , cm


   .Vậy x = 1,2
25 5
os( )( )
3 6
c t cm
 
.Đáp án A. 
Ví dụ 5: Cho đồ thị vận tốc như hình vẽ. Phương trình dao động tương ứng là: 
 A. x = 8cos(t) cm 
 B. x = 4cos(2t -

2
) cm 
 C. x = 8cos(t -

2
) cm 
 D. x = 4cos(2t +

2
) cm 
Hướng dẫn giải: 
Tính chu kì của dao động : Xem sơ đồ giải nhanh. 
 x 
Vận tốc: 
0 0 max
2
v
max 3
2
v
max
2
v
max 3
2
v
max
2
v
max
2
v
O 
Ly độ: 
 x A 0 A
3
2
A 3
2
A2
2
A
2
A 2
2
A
2
A
24
T
12
T
24
T
24
T
24
T
12
T
12
T
12
T
Ly độ: 
 x A 0 A
3
2
A 3
2
A2
2
A
2
A 2
2
A
2
A
4
T
12
T
 x 
Vận tốc: 
0 0 max
2
v
max 3
2
v
max
2
v
max 3
2
v
max
2
v
max
2
v
O 
maxv
8
t(s) 
0 
v(cm/s) 
8
2
3
4
Hình ví dụ 5 
Hình ví dụ 4 
10 
5 
-10 
0 
v(cm/s) 
t(s) 0,1 
7 
t (s) 
v (cm/s) 
40 
20 3 
5
12
-Từ đồ thị ta thấy vật lúc đầu có vận tốc cực đại (VTCB) và giảm về 0 (vị trí biên dương x= A) rồi theo chiều âm đến 
vị trí có v = -8π /2 = - vmax/2 ( 
3
2
x A ) với thời gian tương ứng là 2/3 s. 
-Theo sơ đồ giải nhanh( xem sơ đồ trên) ta có: T/4 + T/12 =2/3 s => T =2s => ω = π rad/s. 
-Tính biên độ: A= vmax/ω =8π /π =8cm . 
-Tính pha ban đầu: Dễ thấy vật lúc đầu ở VTCB và chuyển động theo chiều dương nên  = -π/2. 
Vậy: x = 8cos(t - π/2) cm . Đáp án C. 
Ví dụ 6: Vận tốc của một vật dao động điều hòa biến thiên theo đồ thị như hình vẽ. Lấy π2 = 10, phương trình dao 
động của vật là 
 A. x = 2 10 cos(2πt + 
3

) cm. 
 B. x = 2 10 cos(πt + 
3

) cm. 
 C. x = 2 10 cos(2πt - 
3

) cm. 
 D. x = 2 10 cos(πt - 
3

) cm. 
Hướng dẫn giải: 
Lúc t = 0: v = 20 3 
3
sin
2
   và do vận tốc đang giảm nên vật ở li độ dương và đang đi về biên 
dương. cos
3 3 2
A
x A
 

 
       
 
. 
Thời gian tương ứng từ x = 
2
A
 đến vị trí biên dương rồi về vị trí cân bằng theo chiều âm lần thứ nhất (góc quét 
π/3+π/2): 
5
1 2
6 4 12
T T
t T         rad/s => Biên độ 
40 20
2 10
2
maxvA cm
  
   
Vậy : x = 2 10 cos(2 )
3
t

  cm. Đáp án C. 
Ví dụ 7: Một chất điểm dao động điều hoà hàm cosin có gia tốc biểu diễn như hình vẽ sau. Phương trình dao động 
của vật là: 
A.  10 os
3
x c t cm


 
  
 
 B.  20 os
2
x c t cm


 
  
 
C.   20 osx c t cm D. 20
2
x cos( t )( cm )

  
Hướng dẫn giải: 
 Gọi phương trình dao động của vật có dạng:  cosx A t   . Khi đó phương trình vận tốc và phương trình gia 
tốc có biểu thức lần lượt là:  sinv A t     ;  2 osa A c t     
Từ đồ thị, ta có: T = 2s 
2
( / )rad s
T

    ; 2 axax 2 2
200
20mm
a
a A A cm
 
     . 
Khi t = 0 ta thấy a= 0 và gia tốc đang tăng. => li độ x = 0 và đang đi theo chiều âm 
2
t(s) 
0 
a(m/s2 ) 
2
1
2 0,5
1,5
Hình ví dụ 7 
8 
( Vì x và a ngược pha) => Pha ban đầu của x là: = π/2 
Vậy phương trình dao động của vật là: 20
2
x cos( t )( cm )

  .Đáp án D 
Cách khác: Khi t = 0 
20 00
0 0 20
a cosA cos
v sinsin
  

 
   
     
   
Vậy phương trình dao động của vật là: 20
2
x cos( t )( cm )

  .Đáp án D. 
Ví dụ 8: Cho đồ thị ly độ của một dđđh. Lấy: 
2 10  . 
Hãy viết phương trình gia tốc: 
A.
231 6
4
a , cos( t )m / s

  B. 21 6 2
4
a , cos( t )m / s

  
 C. 
231 6 2
4
a , cos( t )m / s

  D. 21 6 2
4
a , cos( t )m / s

  
Hướng dẫn giải: 
-Chu kì dao động : Theo số liệu trên đồ thị thì vật từ 0
4
2 2
2 2
A
x    đến x= A mất thời gian T/8. 
 Suy ra: T/8=1/8 (s ) => T =1(s) => ω =2π rad/s 
-Biên độ dao động : A =4cm. 
-Vị trí ban đầu : t =0 thì 00
4 1 2
2 2
22 2 2
xA
x cos
A
       Và x đang giảm 
=> Pha ban đầu :  =π/4=>Phương trình li độ: 4 2 4x Acos( t ) cos( t / )(cm)       
-Phương trình gia tốc có dạng: 
2 2a Acos( t ) Acos( t )            
=> 
2 2 232 4 2 1 6 2
4 4
a ( ) . cos( t )c m / s , cos( t )m / s
 
        .Đáp án A. 
Ví dụ 9: Cho dđđh có đồ thị như hình vẽ. PTDĐ tương ứng là: 
A. x = 5cos(2t - 2/3) cm 
B. x = 5cos(2t + 2/3) cm 
C. x =5cos(t + 2/3) cm 
D. x = 5cos(t-2/3) cm 
Hướng dẫn giải: 
Quan sát đồ thị ta thấy: A=5cm 
5
1
12 6 4
T T
T s    
Tại thời điểm t = 0 thì x = - 2,5cm= - A/2 và dốc xuống có nghĩa là vật đang chuyển động theo chiều âm tới vị trí 
biên âm nên 
2
3

  . Vậy x = 5cos(2t + 2/3) cm. Đáp án B. 
4
t(s) 
0 
x(cm) 
4
3
8
5/8 
1
8
2 2
Hình ví dụ 8 
5 
0 
-2,5 
x (cm) 
t (s) 
- 5 
11/12 5/12 
9 
Ví dụ 10: Một vật dao động điều hòa có đồ thị gia tốc như hình. Lấy π2 =10. Phương trình dao động của vật 
là 
A. x = 2,5cos(πt - 
6

) (cm). 
B. x = 5cos(2πt + 
2
3
 ) (cm). 
C. x = 1,25cos(4πt + 
2
3
 ) (cm). 
D. x = 125cos(
5
2
t - 
2
3
 ) (cm). 
Hướng dẫn giải: 
+ Ban đầu chất điểm ở M0 nên  = 2π/3 rad. 
+ 
6
5
23
0

 OMM   =(M0OM) /t = 4π rad/s. 
+ A = a/2 = 1,25cm. Đáp án C. 
Ví dụ 11: Một vật có khối lượng 400g dao động điều hoà có đồ thị động năng như hình vẽ. Tại thời điểm 0t  vật đang 
chuyển động theo chiều dương, lấy 2 10  . Phương trình dao động của vật là: 
A. )()6/cos(10 cmtx   
B. )()3/cos(10 cmtx   
C. )()3/2cos(5 cmtx   
D. )()3/2cos(5 cmtx   
Hướng dẫn giải: 
* Từ các sơ đồ giải nhanh ta có các kết quả sau và áp dụng: 
2
A
x   : Wđ = 3Wt = 
3
W
4
->
3
:
2
A
x   Wđ = 
t
1
W
3
 = 
1
W
4
* Từ vòng tròn lượng giác: nếu 
3

  hoặc 
6

  : động năng đang tăng 
 Từ đồ thị: t = 0: động năng đang giảm  loại phương án A,C. 
* Giả sử phương trình có dạng: x A cos( t )   
t = 0: Wđ = 
3
W
4
 
1
cos os
2 2
A
x A c       : Theo đề suy ra: =-π/3. 
Tính biên độ: Ta có vật từ x0 = A/2 đến A: 
1
1 2
6 6
T
s T s rad / s      ; 
Ta có:
2 21
2
W m A =>
1 2 1 2 0 02 1 1 1
5
2 0 4 2 10 20
W . ,
A m cm
m ,  
     
Vậy: )()3/2cos(5 cmtx   .Đáp án D 
Ví dụ 12: Đồ thị biểu diễn sự biến thiên của gia tốc theo li độ trong dao động điều hoà có dạng là 
 A. đoạn thẳng. B. đường thẳng. 
C. đường hình sin. D. đường parabol. 
Ta có: 
2 2x Acos( t ) v Asin( t ) a Acos( t ) a .x                   
Vậy quan hệ giữa gia tốc và li độ là quan hệ bậc nhất. Mà 
  2 2x A;A a A; A        vậy đáp án đúng là A. đoạn thẳng 
O 
Wđ(J) 
t(s) 
0,015 
0,02 
1/6 
x a 
M0 
200 
100 
M 
2π/3 
Hình vd 10 
200
t(s) 
0 
a(cm/s2) 
200
5
24
100
10 
7: TRẮC NGHIỆM: 
Câu 1: Đồ thị li độ của một vật cho ở hình vẽ bên, phương trình nào 
dưới đây là phương trình dao động của vật 
 A. x = Acos(
2
2 
t
T
) B. x = Asin(
2
2 
t
T
) 
 C. x = Acos t
T
2
 D. x = Asin t
T
2
Câu 2: Đồ thị li độ của một vật cho ở hình vẽ bên, phương trình nào 
dưới đây là phương trình dao động của vật 
 A. x = 5cos(πt+π/2) (cm) B. x = 5sin(πt) (cm) 
 C. x = 5cos(2πt-π/2) (cm) D. x = 5cos2πt (cm) 
Câu 3: Đồ thị biểu diễn dao động điều hoà ở hình vẽ dưới ứng với phương trình dao động nào sau đây: 
 A. x = 3sin( 2 t+
2

) cm B. x = 3cos(
2
3

t+
3

) cm 
 C. x = 3cos( 2 t-
3

) cm D. x = 3sin(
2
3

t+
2

) cm 
Câu 4. Đồ thị biểu diễn dao động điều hòa ở hình vẽ bên ứng với phương trình dao động nào sau đây: 
 A. 6 2
3
x .cos( t )

  (cm) 
 B. 6
3
x .cos( t )

  (cm) 
 C. 6cos( )
3 3
x t
 
  (cm) 
 D. 6cos( )
3
x t

  (cm) 
Câu 5: Quả nặng có khối lượng 500g, gắn vào con lắc lò xo có độ cứng 50N/m. Chọn gốc toạ độ tại vị trí cân bằng, 
kích thích để cho quả nặng dao động điều hoà. Đồ thị biểu diễn li độ theo thời gian như hình vẽ. Phương trình dao 
động của vật là 
 A.x = 8cos(10t -/3)(cm). 
 B. x = 8cos(10t +/3)(cm). 
 C. x = 8cos(10t +/6)(cm). 
 D. x = 8cos(10t -/6)(cm). 
Câu 6: Cho đồ thị x(t) của một dao động điều hòa như hình vẽ. Hãy viết phương trình ly độ: 
A. x = 4cos( t +
4

) B. x = 4cos( t -
4

) 
C. x = 4cos(2 t +
4

) D. x = 4cos(2 t -
4

) 
Câu 7. Đồ thị biểu diễn li độ x của một dao động điều hòa theo thời gian như hình bên. Tại thời điểm t = 
4
T3
 vật có 
vận tốc và gia tốc là: 
 A. v = 0 ; a = ω2A. 
 B. v = -ωA; a = 0. 
 C. v = ωA ; a = 0. 
 D. v = 0; a = 0. 
 x Acos( .t )   
 t (s) 
 T/ 4 
 T/ 4 
 3T/4 
 T 
A 
A 
x 
O 
T 
o 
3 
-3 
 1,5 
1
6
x(cm) 
t(s) 
x 
A 
t 
 O T 
-A 
x(cm) 
5 
t(s) 
 O 1 
-5 
O 
8 
4 
-4 
8 
x (cm ) 
t 
- 
4
t(s) 
0 
X (cm) 
4
3
4
5/4 
1
4
2 2
Hình câu 6 
6
t(s) 
0 
x (cm) 
6
1
3
4
3
Hình câu 4 
7
3
3
11 
Câu 8: Một vật dao động điều hòa có đường biểu diễn sự phụ thuộc vận tốc theo thời gian như hình vẽ. Phương trình 
vận tốc của vật là: 
A. v = 10π
25 5
3 6
cos( )( cm / s )
 
 
B. v= 10π
25
3 6
cos( )( cm / s )
 
 
C. v= 10π
25
3 3
cos( )( cm / s )
 
 
D. v= 10π
25
3 6
cos( )( cm / s )
 