Chuyên đề Giới hạn - Hàm số liên tục

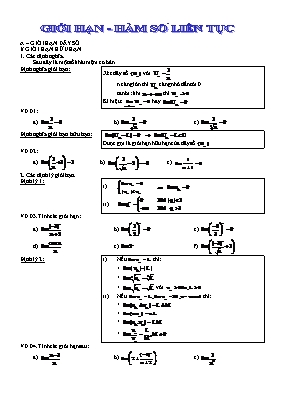
A – GIỚI HẠN DÃY SỐ
I/ GIỚI HẠN HỮU HẠN
1. Các định nghĩa.
	Sau đây là một số khái niệm cơ bản.
Định nghĩa giới hạn: 
Xét dãy số với 
	n càng lớn thì càng nhỏ dần tới 0
	ta nói: khi thì 
Kí hiệu: hay .
VD 01:
	a) 	b) 	c) .
Định nghĩa giới hạn hữu hạn:
Được gọi là giới hạn hữu hạn của dãy số .
VD 02:
	a) 	b) 	c) .
2. Các định lý giới hạn.
Định lý 1:
i) 	 .
ii)	.
VD 03. Tính các giới hạn:
	a) 	b) 	c) 
	d) 	e) 	f) .
Định lý 2:
i) 	Nếu thì:
	+ 
	+ 
	+ với 
ii)	Nếu thì:
	+ 
	+ 
	+ 
	+ 
VD 04. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 	f) 
	g) 	h) 	i) 
	j) 	k) 	l) .
II/ GIỚI HẠN VÔ CỰC
1. Một số giới hạn vô cực cơ bản.
i)	
ii)	
iii)	hay .
2. Các quy tắc tính giới hạn vô cực.
Quy tắc 1:
VD 05. Tính các giới hạn sau:
	a) 	b) 	c) .
Quy tắc 2: 
, dấu của L
+
+
–
–
VD 06. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 	f) 
HD: Tử tách bậc cao nhất của tử, mẫu tách bậc cao nhất của mẫu.
Quy tắc 3: 
, dấu của 
+
+
–
+
+
–
–
–
VD 07. Tính các giới hạn sau:
	a) 	b) 	c) 
HD: Chia cả tử và mẫu cho bậc cao nhất.
VD 08. Tính các giới hạn sau:
	a) 	b) 	c) 
LUYỆN TẬP (Các dạng bài tập)
1. Giới hạn dãy số dạng hữu tỉ.
a) Bậc tử < bậc mẫu (giới hạn = 0): Tách bậc cao nhất.
VD 09. Tính các giới hạn sau:
	a) 	b) 	c) 
b) Bậc tử = bậc mẫu (giới hạn = a/b): Tách bậc cao nhất.
VD 10. Tính các giới hạn sau:
	a) 	b) 	c) 
c) Bậc tử > bậc mẫu (giới hạn =):
VD 11. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e)	f) 
2. Giới hạn dãy số chứa căn thức.
Ø Dạng liên hợp:
Ø Dạng vô định:
	Tách bậc cao nhất.
	–	Nhân lượng liên hợp rồi tách bậc cao nhất.	
VD 12. Tính các giới hạn sau:
 	a) 	b) 	c) 
	d) 	e) 	f) 
	g) 	h) 	i) 
3. Giới hạn dãy số chứa hàm lượng giác.
Áp dụng định lí: 	 .
VD 13. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 	f) 
	g) 	h) 	i) 
	j) 	k) 	l) 
m) 	n) 	o) 
p) 	q) 	r) 
4. Giới hạn dãy số chứa hàm số mũ.
Áp dụng định lí:	.
VD 14. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 	f) 
	g) 	h) 	i) .
5. Một số giới hạn khác.
VD 15. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 
6. Tổng cấp số nhân lui vô hạn.
Định nghĩa:
	với u1 là số hạng đầu tiên và q là công bội (|q|<1)
VD 16:	a) Tìm tổng của cấp số nhân: 
	b) Biểu diễn các số 0,77777(7); 0,313131313131(31) dưới dạng phân số.
	c) Tìm số hạng đầu và công bội của cấp số nhân lùi vô hạn, biết u2 = và tổng là 15.
B – GIỚI HẠN HÀM SỐ 
I/ Các định lí giới hạn.
Một số giới hạn cơ bản:
	,
Định lí 1:
Cho , khi đó:
	+ 
	+ 
	+ 
	+ 
VD 17. Tính các giới hạn sau:
 	a) 	b) 	c) 
	d) 	e) 	f) 
	g) 	h) 	i) 
Định lí 2:
Cho , khi đó:
	+ 
	+ 
	+ thì 
VD 18. Tính các giới hạn sau:
 	a) 	b) 	c) 
	d) 	e) 	f) 
II/ Giới hạn một bên
* Một vài khái niệm:
i) Nếu thì hàm số có giới hạn bên phải và bên trái tại xo và 
ii) Ngược lại: thì hàm số có giới hạn tại điểm xo và 
iii) Các định lí 1, định lí 2 vẫn đúng trong giới hạn 1 bên.
VD 19. Tìm với .
VD 20. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 	f) 
	g) 	h) 	i) 
VD 21. 	a) Cho .
	Tìm giới hạn của khi (nếu có).
	b) Cho .
	Tìm giới hạn của khi (nếu có).
VD 22. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 	f) 
III/ Quy tắc tìm giới hạn vô cực
1. Giới hạn cơ bản:	
2. Các quy tắc tính giới hạn vô cực.
Quy tắc 1: 
Dấu của L
+
+
–
–
VD 23. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 	f)
Quy tắc 2:
Dấu của L
Dấu của g(x)
+
+
–
+
+
–
–
–
VD 24. Tính các giới hạn sau:
	a) 	b) 	c) 
	d) 	e) 	f) 
IV/ Một vài giới hạn khác.
VD 25. Tính các giới hạn sau:
	a) 	b) 	c) 
LUYỆN TẬP (Các dạng vô định)
1. Dạng : Tách nhân tử chung (hoặc nhân liên hợp rồi tách nhân tử)
VD 26. Tính các giới hạn sau:
 	a) 	b) 	c) 
	d) 	e) 	f) 
	g) 	h) 	i) 
	j) 	k) 	l) 
2. Dạng : Chuyển về dạng 
VD 27. Tính các giới hạn sau:
	a) 	b) 	c) 
3. Dạng : Nhân liên hợp
VD 28. Tính các giới hạn sau:
	a) 	b) 	c) 
BÀI TẬP (Bài tập tự rèn luyện).
1. Tính các giới hạn sau:
	g) 	h) 	i) 
	j) 	k) 	l) 
	m) 	n) 	o) 
	p) 	q) 	r) 
2. Tính các giới hạn sau:
	g) 	h) 	i) 	j) 	k) (nếu có)	l) 
	m) 	n) 	o) 	p) 	q) 	r) 
3.Tính các giới hạn sau:
	g) 	h) 	i) 
	j) 	k) 	l) 
	m) 	n) 	o) 
C – HÀM SỐ LIÊN TỤC
ĐN: 	Nếu thì liên tục tại điểm xo, ngược lại gọi là gián đoạn tại xo.
	 liên tục tại mọi điểm thuộc tập J thì nó liên tục trên J.
	 liên tục trên liên tục trên và 
VD: 	Xét tính liên tục của hàm tại điểm 
Cm liên tục trên 
Xét tính liên tục của hàm số 
Cm 
J Chú ý:	
i) Tổng, hiệu, tích, thương (giá trị mẫu tại xo phải khác 0) của 2 hàm liên tục tại điểm xo là những hàm liên tục tại xo. 
	ii) liên tục tại xo, liên tục tại thì hàm liên tục tại xo 
	iii) Hàm đa thức và liên tục trên tập xác định của chúng
	iv) Đồ thị của hàm liên tục là một đường liền nét.
VD: Xét tính liên tục của hàm 
	Xét tính liên tục của hàm 
Theo dõi hình để thấy tính liên tục của các hàm số:
J Định lí (về giá trị trung gian của hàm số liên tục): 
f liên tục trên vàthì tồn tại ít nhất một điểm sao cho 
VD: Cm có ít nhất một nghiệm nhỏ hơn 1
VD:	Xét tính liên tục của hàm số tại điểm 
Xét tính liên tục của hàm số 
Chứng minh có ít nhất 1 nghiệm thuộc 
Tìm a để liên tục tại 
Tìm a để liên tục trên 
Chứng minh có ít nhất 1 nghiệm
D – LUYỆN TẬP
	Đây là các bài tập tự làm, thầy chỉ hướng dẫn giải một số bài cho các em, yêu cầu các em phải tự làm hoàn thành để thầy kiểm tra sau khi dạy xong phần giới hạn.
	Không còn nhiều thời gian nữa, các kì thi đã đến gần, tương lai của các em phụ thuộc vào chính nỗ lực của bản thân các em. Nếu các em không chăm chỉ thì thầy cũng đành pó tay thui! Hãy cố gắng lên.
1. Tìm các giới hạn sau:
2. Tìm các giới hạn sau:
3. Tìm các giới hạn sau: 
4. Tìm các giới hạn sau:
5. Tính:
 với 	 với 
6. Tính tổng: và 
7. Trong các hình vuông cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp để được 1 hình vuông, tiếp tục nối như thế với hình vuông mới để được hình vuông tiếp theo và cứ tiếp tục quá trình trên mãi. Tính tổng của các hình vuông được tạo thành (hình vẽ).
4. Biểu diễn số 0,2525252(25); 0,50111(1); 17,2354141(41) dưới dạng phân số
8. Tổng CSN lùi vô hạn là , tổng 3 số hạng đầu là . Tìm số hạng đầu và công bội của CSN trên.
9. Tìm các giới hạn sau:
10. Tính 
 biết 	 biết 
 biết 	 biết 
 biết 	 biết 
11. Tìm các giới hạn sau:
12. Cho hàm số:
	Tính giới hạn của hàm số tại -2 và tại 1
	Tính giới hạn của hàm số khi 
	Tìm a để hàm số có giới hạn tại 1
	Tìm a để hàm số có giới hạn tại 1
	Tìm a để hàm số có giới hạn tại 0
13. Chứng minh rằng:
	Liên tục trên R
	Liên tục tại x = 1
	Liên tục khi trên đoạn 
	Liên tục khi a = 2 trên R
14. Cho hàm số:
	Tìm a để hàm số liên tục tại 2
	 Tìm a để hàm số liên tục tại 4
	Tìm a để hàm số liên tục tại 2
	Tìm a để hàm số liên tục tại 0
	Xét tính liên tục của hàm số tại 0 và tại 1
	Xét tính liên tục của hàm số tại 0 và tại 4
15. Tìm các điểm gián đoạn của các hàm số sau:
16. Tìm m để phương trình sau có nghiệm
17. Chứng minh phương trình:
	luôn có nghiệm
	luôn có nghiệm
	có ít nhất 2 nghiệm
	có ít nhất 2 nghiệm trong 
	có ít nhất 1 nghiệm với mọi m
	có nghiệm trong khoảng 
	có đúng 1 nghiệm trong khoảng
	có đúng 1 nghiệm trong khoảng 
E – ÔN TẬP
1. 
2. 
3. Biểu diễn số 0,565656(56); 0,571222(2) dưới dạng phân số
4.Cho CSN với 
a) Tìm công bội q
b) Tổng của CSN trên là , tìm (số hạng đầu tiên của CSN)
5.