Câu hỏi trắc nghiệm về Hàm số - Đề số 3

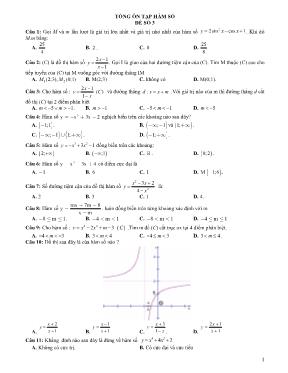
 1 
TỔNG ÔN TẠP HÀM SỐ 
ĐỀ SỐ 3 
Câu 1: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 22sin cos 1y x x   . Khi đó 
M.m bằng: 
A. 25
4
 B. 2 . C. 0 D. 
25
8
Câu 2: (C) là đồ thị hàm số 2 1
1
xy
x



. Gọi I là giao của hai đường tiệm cận của (C). Tìm M thuộc (C) sao cho 
tiếp tuyến của (C) tại M vuông góc với đường thẳng IM 
A. 1 2(2;3), (0;1)M M B. M(2;3) C. không có D. M(0;1). 
Câu 3: Cho hàm số : 2 1 ( )
1
xy C
x



 và đường thẳng :d y x m  .Với giá trị nào của m thì đường thẳng d cắt 
đồ thị (C) tại 2 điểm phân biệt 
A. 5 1m m     . B. 1m   C. 5 1m    D. 5m   
Câu 4: Hàm số 3 3 2y x x    nghịch biến trên các khoảng nào sau đây? 
A.  1;1 . B.   ; 1 và  1; . 
C.    ; 1 1;    . D.  1;  . 
Câu 5: Hàm số 3 23 1y x x    đồng biến trên các khoảng: 
A.  2; B.  ;1 C.  . D.  0;2 . 
Câu 6: Hàm số 3 3 4y x x   có điểm cực đại là 
A. 1 B. 6 C. 1 D.  1;6M . 
Câu 7: Số đường tiệm cận của đồ thị hàm số 
2
2
3 2
4
x xy
x
 


 là: 
A. 2 B. 3 C. 1 D. 4. 
Câu 8: Hàm số 7 8mx my
x m
 

. luôn đồng biến trên từng khoảng xác định với m 
A. 8 1m   . B. 4 1m   C. 8 1m   D. 4 1m   
Câu 9: Cho hàm số :  4 22 3y x x m C    .Tìm m để (C) cắt trục ox tại 4 điểm phân biệt. 
A. 4 3m    B. 3 4m  C. 4 3m   D. 3 4m  . 
Câu 10: Đồ thị sau đây là của hàm số nào ? 
A. 1
2



x
xy 
B. 1
1



x
xy 
C. x
xy



1
3
.
D. 1
12



x
xy 
Câu 11: Khẳng định nào sau đây là đúng về hàm số 4 24 2y x x   
A. Không có cực trị. B. Có cực đại và cực tiểu 
 2 
C. Đạt cực tiểu tại x = 0. D. Có cực đại, không có cực tiểu 
Câu 12: Cho hàm số     y x mx m x3 22 ( 3) 4 mC( ) . Giá trị của tham số m để đưởng thẳng  d y x( ) : 4 cắt 
mC( ) tại ba điểm phân biệt A(0;4), B, C sao cho tam giác KBC có diện tích bằng 8 2 với điểm K(1;3) là 
A. 

m 1 137
2
B. 

m 1 137
2
C. 

m 1 137
2
D. 
 
m 1 137
2 .
Câu 13: Cho hàm số
3
2( 2) (4 8) 1
3
xy m x m x m      
 . Để hàm số đạt cực trị tại 1x , 2x thỏa mãn 
1 22x x   thì 
A. 
3 2
2
m 
 B. 
3
2
m 
 C. 2m   6m  D. 2 6m  . 
Câu 14: Số giao điểm của đồ thị hàm số 3 23 1y x x   và đường thẳng : 1d y là 
A. 3 . B. 2 . C. 1 . D. 4 . 
Câu 15: Cho hàm số: mmxxxy  23 3 . Giá trị m để hàm số nghịch biến trên một khoảng có độ dài bằng 
3 trên trục số là: 
A. 3 / 4m   B. 3 / 4m  C. 3m  D. 3m  . 
Câu 16: Bảng biến thiên sau đây là của hàm số nào? Chọn 1 câu đúng. 
A. 13 23  xxy B. 13 23  xxy C. 13 23  xxy D. 13 23  xxy . 
Câu 17: Tập xác định của hàm số 2017
2 3
y
x


 là: 
A. 3\ -
2
D    
 
 B.  \ 3D   . C. 3\
2
D    
 
 . D.  \ 3D   
Câu 18: Câu 116. Một màn ảnh chữ nhật cao 
1,4m được đặt ở độ cao 1,8m so với tầm mắt (tính 
đầu mép dưới của màn hình).Để nhìn rõ nhất phải 
xác định vị trí đứng cách màn ảnh sao cho góc 
nhìn lớn nhất.Hãy xác định vị trí đó. 
A. 2,4m. B. 2,43m C. 2,41m D. Đáp án khác 
Câu 19: Phương trình tiếp tuyến với đồ thị hàm số 1
1
xy
x



 song song với đường thẳng : 2 1 0x y    là: 
A. 2 7 0x y   B. 2 0x y  C. 2 1 0x y    . D. 2 7 0x y   
Câu 20: Hàm số 3 23 1y x x    đồng biến trên khoảng nào ? 
A.   ;  . B.  2 ;0 C.  0 ;2 D.   ;0 
 3 
Câu 21: Cho hàm số   3 2 2 33y x m x m có đồ thị  C . Tìm tất cả các giá trị thực của tham số m để tiếp 
tuyến của đồ thị  C tại điểm có hoành độ 0 1x  song song với đường thẳng : 3 .d y x  
A. Không có giá trị của m . B. 1m   . 
C. 
   
1
1
m
m
. D.  1m . 
Câu 22: Tiếp tuyến của đồ thị hàm số 3 23 2y x x   tại điểm  1; 2A   là 
A. 9 2y x  B. 24 7y x  C. 24 2y x  D. 9 7y x  . 
Câu 23: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 4 2 42 2y x mx m m    có ba 
điểm cực trị tạo thành một tam giác đều. 
A. 3m   B. 3 3m  C. 3m  . D. 3m  
Câu 24: Tìm giá trị cực tiểu CTy của hàm số 
4 22 1.y x x   
A. CTy = -1 B. CTy =1 C. CTy = 0 D. CTy = -2. 
Câu 25: Hàm số      3 2 21 3 2 2f x x m x m m x       đạt cực tiểu tại 2x  khi 
A. 2m  B. 1m  . C. 3m  D. 5 
Câu 26: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2 5y x x x   trên đoạn  0;2 lần lượt là: 
A. 1; 0 B. 2; 1 C. 3; 1 D. 2; 3 . 
Câu 27: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số
2 1
2 1
mx mxy
x
 


 có hai tiệm cận 
ngang. 
A. m = 0 
B. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài. 
C. m < 0. 
D. m > 0. 
Câu 28: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 23 1y x x x    trên đoạn  1;2 lần lược là: 
A. 21 ; 0 B. 619 ; 
9
 C. 4 621 ; 
9
 D. 621 ; 
9
 . 
Câu 29: Hàm số    3 23 1 3 1 1y x m x m x      . luôn đồng biến trên  với m 
A. 1 0   m m B. 1 0  m . C. 1 0   m m D. 1 0m   
Câu 30: Số cực trị của hàm số 4 23 3y x x   là: 
A. 4 B. 2. C. 3 D. 1 
Câu 31: Tìm điểm cực đại của đồ thị hàm số 3 23 1y x x   ? 
A.  2; 3 B.  0;1 C.  0;2 D.  1;0 . 
Câu 32: Giá trị m để hàm số : 3 23 ( 1) 4y mx mx m x     không có cực trị là : 
A. 10
4
  m m B.  
1
0
4
m C. 10
4
  m m D.  
1
0
4
m . 
Câu 33: Cho hàm số 2mx my
x 1



 . Với giá trị nào của m thì đường tiệm cận đứng , tiệm cận ngang của đồ 
thị hàm số cùng hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8. 
A. m 2 B. m 2  C. m 4  D. 1m
2
  . 
Câu 34: Cho hàm số 

2
1
x
y
x
. Xét các mệnh đề sau: 
 4 
 1) Hàm số đã cho nghịch biến trên    ;1 1;   . 
 2) Hàm số đã cho đồng biến trên  ;1 . 
 3) Hàm số đã cho nghịch biến trên tập xác định. 
 4) Hàm số đã cho nghịch biến trên các khoảng  ;1 và  1; . 
 Số mệnh đề đúng là 
A. 3 B. 2 C. 4 D. 1 . 
Câu 35: Cho 2016 ( )
1
xy C
x



 .Giao điểm của (C) với trục oy là : 
A. M(0,2016) B. M(0,-2016) C. M(2016,0). D. M(-2016,0) 
Câu 36: Hàm số 2 3 2y x x   có bao nhiêu điểm cực trị? 
A. 1 . B. 2 . C. 3 . D. 0 . 
Câu 37: Tìm giá trị lớn nhất của hàm số 
2 4x
y
x
 trên đoạn    1;3 . 
A. 
1;3
max 5y
   
 B. 
1;3
16
max
3
y
   
 C. 
   

1;3
max 4y D. 
1;3
13
max
3
y
   
 . 
Câu 38: Cho hàm số  y f x có đồ thị như hình bên. 
Tìm tất cả các giá trị thực của tham số m để phương 
trình   2f x m  có bốn nghiệm phân biệt. 
A. 4 3m   . B.   4 3m . C. 6 5m   . D.   6 5m . 
Câu 39: Cho hàm số    3 23 1f x x x . Số nghiệm của phương trình    0f f x  là? 
A. 7 . B. 6 . C. 9 . D. 3 . 
Câu 40: Đường cong trong hình bên là đồ thị của 
một hàm số trong bốn hàm số được liệt kê ở bốn 
phương án A, B, C, D dưới đây. Hỏi đó là hàm số 
nào? 
A.   3 23 1y x x . B. 3 23 1y x x    . C. 3 23 1y x x   . D.    3 3 1y x x . 
Câu 41: Hàm số 2 tan
tan 1
x my
x



 đạt giá trị lớn nhất trên 0;
4
 
  
 bằng 1 khi 
A. m=1 B. m=2. C. m=-1 D. m=0 
Câu 42: Cho hàm số  y f x xác định trên tập .D Trong các mệnh đề sau mệnh đề nào đúng? 
A.   max
D
M f x nếu  f x M với mọi x thuộc D . 
 5 
B.  min
D
m f x nếu  f x m với mọi x thuộc D . 
C.  min
D
m f x nếu  f x m với mọi x thuộc D và tồn tại 0x D sao cho  0f x m . 
D.  max
D
M f x nếu  f x M với mọi x thuộc D và tồn tại 0x D sao cho  0f x M . 
Câu 43: Một trang chữ của một quyển sách tham khảo Văn học cần diện tích 384 cm2. Biết rằng trang giấy 
được canh lề trái là 2cm, lề phải là 2 cm, lề trên 3 cm và lề dưới là 3 cm. Trang sách đạt diện tích nhỏ nhất thì 
có chiều dài và chiều rộng là: 
A. 32cm và 12 cm B. 30 cm và 20 cm. C. 40 cm và 20 cm D. 24 cm và 16 cm 
Câu 44: Tìm tất cả các giá trị thực của tham số m để phương trình       24 2 2 1x x m x x có 
hai nghiệm phân biệt. 
A. 10;14m      . B.    10;13 14m   . 
C.    10;13 14m . D.     10;13m . 
Câu 45: Xét các mệnh đề sau: 
 1) Đồ thị hàm số 1
2 3
y
x
 
 có hai đường tiệm cận đứng và một đường tiệm cận ngang. 
 2) Đồ thị hàm số 
2 1x x x
y
x
   có hai đường tiệm cận ngang và một đường tiệm cận đứng. 
 3) Đồ thị hàm số 
2
2 1
1
x x
y
x
 

 có một đường tiệm cận ngang và hai đường tiệm cận đứng. 
 Số mệnh đề đúng là 
A. 2 . B. 3 . C. 1 . D. 0 . 
Câu 46: Hàm số   4 22 1y x x có mấy điểm cực trị? 
A. 0 . B. 1 . C. 2 . D. 3 . 
Câu 47: Phương trình đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 2 1
1
x
y
x
 
 lần lượt là 
A. 1; 2x y  . B.  1; 2y x . C. 1; 2x y   . D. 1; 2x y   . 
Câu 48: Đồ thị hàm số 4 22 1y x x    có dạng: 
A. 
-2 -1 1 2
-2
-1
1
2
x
y
 B. 
-2 -1 1 2
-2
-1
1
2
x
y
C. 
-2 -1 1 2
-2
-1
1
2
x
y
 D. 
-2 -1 1 2
-2
-1
1
2
x
y
Câu 49: Giá trị của m để tiệm cận đứng của đồ thị hàm số 2 1xy
x m



 đi qua điểm M(2 ; 3) là. 
A. 3 B. 2 C. -2. D. 0 
Câu 50: Gọi   2x 1M C : y
x 1

 

 có tung độ bằng 5. Tiếp tuyến của (C) tại M cắt các trục tọa độ Ox, Oy lần 
lượt tại A và B. Hãy tính diện tích tam giác OAB ? 
 6 
A. 123
6
 B. 121
6
 C. 119
6
 D. 125
6
. 
----------------------------------------------- 
----------- HẾT ---------- 
ĐÁP ÁN 
cauhoi dapan cauhoi dapan 
1 C 26 D 
2 A 27 D 
3 A 28 C 
4 B 29 D 
5 D 30 D 
6 A 31 B 
7 A 32 B 
8 C 33 C 
9 B 34 D 
10 D 35 A 
11 C 36 C 
12 C 37 A 
13 B 38 D 
14 B 39 A 
15 B 40 C 
16 A 41 D 
17 A 42 D 
18 A 43 B 
19 A 44 B 
20 C 45 C 
21 B 46 D 
22 D 47 A 
23 B 48 C 
24 D 49 C 
25 A 50 B