Câu hỏi trắc nghiệm Giải tích 12 - Chương II

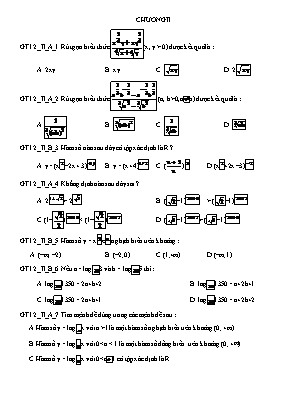
CHƯƠNG II
GT12_II_A_1. Rút gọn biểu thức (x, y > 0) được kết quả là :
	A. 2xy	B. xy	C. 	D. 2
GT12_II_A_2. Rút gọn biểu thức (a, b>0, ab) được kết quả là :
	A.	B. 	C. 	D. 
GT12_II_B_3. Hàm số nào sau đây có tập xác định là R ?
	A. y= (x–2x + 3)	B. y = (x+4)	C. ()	D.(x+2x –3) 
GT12_II_A_4. Khẳng định nào sau đây sai ?
	A. 2> 2	B. (–1)	> (–1)
	C.(1–) (–1)
GT12_II_B_5. Hàm số y = xe nghịch biến trên khoảng :
A. (–¥; –2)	B. (–2;0)	C.(1;+¥)	D.(–¥;1)
GT12_II_B_6. Nếu a = log3 và b = log5 thì :
	A. log1350 = 2a+b+2	B. log1350 = a+2b+1
	C. log1350 = 2a+b+1	D. log1350 = a+2b+2
GT12_II_A_7. Tìm mệnh đề đúng trong các mệnh đề sau :
A.Hàm số y = logx với a >1 là một hàm số nghịch biến trên khoảng (0; +¥) 
B.Hàm số y = logx với 0< a < 1 là một hàm số đồng biến trên khoảng (0; +¥)
C.Hàm số y = logx với 0<a1 có tập xác định là R
D.Đồ thị hai hàm số y = log x và y = logx (0<a1) đối xứng với nhau qua trục hoành
GT12_II_B_8. Hàm số y = xlnx đồng biến trên khoảng :
	A. (0;+¥)	B. (; +¥)	C. (0;1)	D. (0;) 
GT12_II_B_9. Đạo hàm của hàm số y = là :
	A. y/ = 	B. y/ = e+ e	
C. y/ = 	D. y/ = 
GT12_II_B_10. Tập xác định D của hàm số y = loglà :
	A. D = (1;+¥)	B.D = (–¥;10)	
C. D = (–¥;1)È(2;10)	D. D = (2;10)
GT12_II_C_11. Hàm số y = ln(x– 2mx + 4) có tập xác định D = R khi :
	A. m < 2	B. –2 < m < 2	C. m = 2	D. m ³ 2 hoặc m £ –2
GT12_II_A_12. Nếu a> a và log< log thì : 
	A. 01	
C. a > 1 và 01 và b > 1
GT12_II_B_13. Cho a> 0, b>0 thoả a+ b=7ab . Chọn mệnh đề đúng trong các mệnh đề sau :
	A. 3log(a+b)= (loga + logb)	B. log(a+b) = (loga + logb)
	C. 2(loga + logb) = log(7ab)	D. log= (loga + logb)
GT12_II_B_14. Đối với hàm số y = ln, ta có :
A. xy/ + 1 = e	B. xy/ + 1 = –e	C. xy/ – 1 = e	D. xy/ – 1 = – e
GT12_II_C_15. Cho 0<a¹1 và 0<b¹1 và n ÎN*, một học sinh tính biểu thức :
	P = + + ++ theo các bước sau :
P = loga + loga+ loga+ + loga	
(II) 	P = loga.aa
(III) 	P = loga	(IV)	P = n(n+1) loga
	Học sinh trên đã giải sai ở bước nào ?
A. (I)	B. (II)	C.(III)	D.(IV)
GT12_II_B_16. Hàm số y = : 
A. có một cực tiểu	B. có một cực đại	
C. không có cực trị	D. có một cực tiểu và một cực đại
GT12_II_B_17. Số nghiệm của phương trình . Chọn đáp án đúng nhất:
2
1
3
0
GT12_II_B_18. Giải phương trình . Chọn đáp án đúng nhất:
GT12_II_B_19. Giải phương trình . Chọn đáp án đúng nhất:
GT12_II_B_20. Giải phương trình . Chọn đáp án đúng nhất:
Phương trình vô nghiệm
GT12_II_B_21. Giải phương trình . Chọn đáp án đúng nhất:
Phương trình vô nghiệm
GT12_II_B_22. Giải phương trình . Chọn đáp án đúng nhất:
Phương trình vô nghiệm
GT12_II_B_23. Giải bất phương trình . Chọn đáp án đúng nhất:
Bất phương trình vô nghiệm
GT12_II_B_24. Giải bất phương trình . Chọn đáp án đúng nhất:
GT12_II_B_25. Giải bất phương trình . Chọn đáp án đúng nhất:
GT12_II_B_26. Giải bất phương trình . Chọn đáp án đúng nhất:
GT12_II_B_27. Giải bất phương trình . Chọn đáp án đúng nhất:
GT12_II_B_28. Giải bất phương trình . Chọn đáp án đúng nhất:
GT12_II_B_29. Giải bất phương trình . Chọn đáp án đúng nhất:
Bất phương trình vô nghiệm
GT12_II_B_30. Giải bất phương trình . Chọn đáp án đúng nhất:
ĐÁP ÁN
1. B
2. C
3. A
4. D
5. B
6. C
7. D
8. B
9. A
10. C
11. B
12. B
13. D
14. A
15. D
16. B
17. A
18. C
19. D
20. C
21. C
22. B
23. B
24. C
25. A
26. D
27. A
28. D
29. B
30. C
Trong quá trình soạn không tránh khỏi những sai sót. Mong nhận được sự thông cảm và góp ý của quý thầy, cô và bạn bè đồng nghiệp. Xin chân thành cảm ơn.