Câu hỏi trắc nghiệm Giải tích 12 - Chương 1

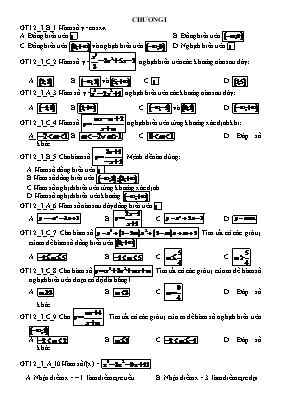
CHƯƠNG I
GT12_I_B_1. Hàm số y=cosx-x
A. Đồng biến trên 	B. Đồng biến trên 
C. Đồng biến trên và nghịch biến trên 	D. Nghịch biến trên 
GT12_I_C_2. Hàm số y= nghịch biến trên các khoảng nào sau đây:
	B. và C. 	D. 
GT12_I_A_3. Hàm số y= nghịch biến trên các khoảng nào sau đây:
 	B. 	C. và 	D. 
GT12_I_C_4. Hàm số nghịch biến trên từng khoảng xác định khi: 
 	B. 	C. 	D. Đáp số khác
GT12_I_B_5. Cho hàm số . Mệnh đề nào đúng:
 A. Hàm số đồng biến trên 	 
 B. Hàm số đồng biến trên 
 C. Hàm số nghịch biến trên từng khoảng xác định 
 D. Hàm số nghịch biến trên khoảng 
GT12_I_A_6. Hàm số nào sau đây đồng biến trên 
 	B. 	C. 	D. 
GT12_I_C_7. Cho hàm số . Tìm tất cả các giá trị của m để hàm số đồng biến trên 
 	B. 	C. 	C. 
GT12_I_C_8. Cho hàm số . Tìm tất cả các giá trị của m để hàm số nghịch biến trên đoạn có độ dài bằng 1
 	B. 	C. 	D. Đáp số khác 
GT12_I_C_9. Cho . Tìm tất cả các giá trị của m để hàm số nghịch biến trên 
 	B. 	C. 	D. Đáp số khác
GT12_I_A_10. Hàm số f(x) = 
	A. Nhận điểm x = – 1 làm điểm cực tiểu	B. Nhận điểm x = 3 làm điểm cực đại
	C. Nhận điểm x = 1 làm điểm cực đại	D. Nhận điểm x = 3 làm điểm cực tiểu
GT12_I_B_11. Hàm số y = 
	A. Nhận điểm x = làm điểm cực tiểu	B. Nhận điểm x = làm điểm cực đại
	C. Nhận điểm x = làm điểm cực đại	D. Nhận điểm x = làm điểm cực tiểu
GT12_I_C_12. Cho hàm số . Mệnh đề nào sau đây là sai?
A. thì hàm số có cực trị	B. thì hàm số có cực đại và cực tiểu
C. Hàm số luôn luôn có cực đại và cực tiểu	D. thì hàm số có hai điểm cực trị
GT12_I_A_13. Số điểm cực trị của hàm số y = là
	A. 1	B. 3	C. 0	D. 2
GT12_I_A_14. Hàm số y = 
A. Nhận điểm x = 3 làm điểm cực tiểu	B. Nhận điểm x = 3 làm điểm cực đại
C. Nhận điểm x = 0 làm điểm cực tiểu	D. Nhận điểm x = 0 làm điểm cực đại
GT12_I_A_15. Hàm số f có đạo hàm là f’(x) = . Số điểm cực tiểu của hàm số là
	A. 0	B. 2	C. 3	D. 1
GT12_I_C_16. Hàm số đạt cực tiểu tại x = – 1 khi
	A. m = –3	B. m = –1	C. m = 0	D. m = 1
GT12_I_B_17. Hàm số có ba điểm cực trị khi giá trị của m là
	A. 	B. 	C. 	D. 
GT12_I_B_18. Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số: là:
	A. 	B. 	C. 	D. 
GT12_I_B_19. Hệ thức liên hệ giữa giá trị cực đại (yCĐ ) và giá trị cực tiểu (yCT ) của đồ thị hàm số y = x3 – 2x là:
	A. 	B. 	C. 	D. 
GT12_I_A_20. Giá trị nhỏ nhất của hàm số trên đoạn [2;3] bằng:
5
3
GT12_I_B_21. Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số . Tổng M + n bằng:
1
1
63
78
GT12_I_C_22. Giá trị tham số m để giá trị nhỏ nhất của hàm số trên đoạn [0;1] bằng 2 là:
Không có giá trị m
GT12_I_C_23. Giá trị tham số m để giá trị nhỏ nhất của hàm số trên đoạn [1;1] bằng 6 là:
Không có giá trị m
GT12_I_A_24. Tiệm cận ngang của đồ thị của hàm số: là
	A. y = – 3	B. x = 1	C. x = 	D. y = 2 
GT12_I_B_25. Số tiệm cận của đồ thị của hàm số: là
	A. 1	B. 2	C. 3	D. 4
GT12_I_B_26. Tất cả tiệm cận của đồ thị của hàm số: là
	A. y = 1 và y = – 1	B. y = – 1	C. x = 1 	D. y = 1
GT12_I_C_27. Tìm m để (C): y = x3 + 3x2 + 3x – 4 cắt d: y = – m + 5 tại đúng một nghiệm dương.
A. m 9	C. 	D. 
GT12_I_C_28. Tìm k để (C): y = – x3 + 3x2 + 1 cắt d: y = k(x + 1) + 5 tại 3 điểm phân biệt
A. k 0	C. 	D. 
GT12_I_C_29. Tìm m để (C): y = x4 – mx2 + m – 1 cắt trục hoành tại 4 điểm phân biệt
A. m 1	C. 	D. 
GT12_I_C_30. Hàm số y= . Giá trị của m để hàm số đồng biến trên :
A. m<1 	B. m=1 	C. m 	D. m 
ĐÁP ÁN
1. D
2. D
3. C
4. A
5. C
6. C
7. C
8. C
9. C
10. D
11. C
12. C
13. B
14. A
15. D
16. A
17. B
18. A
19. A
20. B
21. B
22. A
23. B
24. D
25. B
26. A
27. A
28. C
29. C
30. B
Trong quá trình soạn không tránh khỏi những sai sót. Mong nhận được sự thông cảm và góp ý của quý thầy, cô và bạn bè đồng nghiệp. Xin chân thành cảm ơn.