Các dạng toán ôn thi vào lóp 10

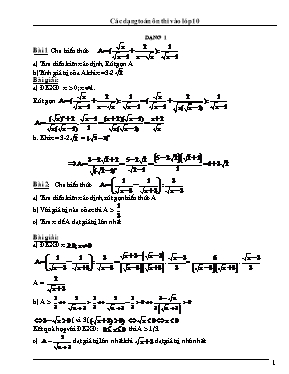
Dạng 1
Bài 1 Cho biểu thức 
a) Tìm điều kiện xác định, Rút gọn A
b)Tính giá trị của A khi x=3-2
Bài giải:
a) ĐKXĐ x > 0; x1.
Rút gọn 
b. Khi x= 3-2 = 
Bài 2: Cho biểu thức 
a) Tìm điều kiện xác định, rút gọn biểu thức A
b) Với giá trị nào của xthì A > 
c) Tìm x để A đạt giá trị lớn nhất
Bài giải:
a) ĐKXĐ x 
.=.
A = 
b) A > 
 ( vì 3( 
Kết quả hợp với ĐKXĐ: thì A > 1/3.
c) đạt giá trị lớn nhất khi đạt giá trị nhỏ nhất.
Mà lúc đó AMax=
Bài 3: Cho biểu thức 
a) Nêu điều kiện xác định và rút gọn biểu thức P
b) Tìm các giá trị của x để P = 
c) Tìm giá trị nhỏ nhất của biểu thức: M
Bài giải:
a) ĐKXĐ x
P = =
b) 
 (TMĐK)
c) = ta có 
Vậy Mmin= 4.
Bài 4: Cho biểu thức: 
a) Tìm ĐKXĐ ,rút gọn biểu thức
b) Tìm x để D < -
c) Tìm giá trị nhỏ nhất của D
Dạng 2
Bài 1 :Cho biểu thức: 
a) Tìm ĐKXĐ, rút gọn P
b) Tìm a để P nhận giá trị nguyên.
Bài giải:
a) ĐKXĐ: a
b) 
để P nhận giá trị nguyên thì nhận giá trị nguyên dương. thuộc ước dương của 2.
 a=1 (Loại vì không thoả mãi điều kiện)
Vậy P nhận giá trị nguyên khi a = 0
Bài 2: Cho biểu thức 
a) Tìm x để B có nghĩa và rút gọn B.
b) Tìm x nguyên để B nhận giá trị nguyên.
Bài giải:
a) ĐKXĐ 
B =
b) B nhận giá trị nguyên khi nhận giá trị nguyên.
 Ư(1)
 thoả mãn điều kiện
Vậy x= -1; x= -3 thì B nhận giá trị nguyên
Bài 3: Cho biểu thức: 
a) Tìm ĐKXĐ , rút gọn P
b) Tìm giá trị nhỏ nhất của P
c) Tìm x để biểu thức nhận giá trị nguyên.
Dạng 3
Bài 1: Cho biểu thức: 
a) Tìm ĐKXĐ và rút gọn P
b) Tìm x để P > 0
Bài giải
a) ĐKXĐ x>0; x
b) P > 0 ( vì 
Kết hợp với ĐKXĐ: thì P > 0
Bài 2: Cho biểu thức: 
a) Tìm ĐKXĐ, rút gọp P
b) Tìm giá trị của a để P > 0
Bài 3 : Cho biểu thức: 
a) Tìm ĐKXĐ, rút gọn P
b) Tìm x để P < 
Bài 4: Cho biểu thức: 
a) Tìm ĐKXĐ, rút gọn P.
b) Tìm x để P <
Bài 5: Cho biểu thức: 
a)Tìm ĐKXĐ, rút gọn B
b)Tìm a để B < 7- 4
Bài 6: Cho biểu thức: 
a) Rút gọn biểu thức K
b) Tìm giá trị của K khi a = 3+2
c) Tìm giá trị của a sao cho K < 0
Dạng 4
Bài 1 : Cho biểu thức: 
a) Tìm ĐKXĐ và rút gọn A
b) Tìm tất cả các giá trị của x sao cho A < 0
c) Tìm tất cả các giá trị của tham số m để phương trình A. có nghiệm.
Bài giải
a) ĐKXĐ: x > 0; x 
b) A < 0 (vì ) kết hợp với ĐKXĐ 0 <x < 1 thì 
A < 0
c) P.t: A.
Đặt >0 ta có phương trình để phương trình (1) có nghiệm thì phương trình (*) phải có nghiệm dương.
Để phương trình (*) có nghiệm dương thì: 
 Vậy m>-1 và m thì pt A có nghiệm.
Bài 2: Cho biểu thức: 
a) Tìm ĐKXĐ và rút gọn P
b) Tìm giá trị của P khi x = 25
c) Tìm x để P.
Bài giải:
a) ĐKXĐ x > 0; x 
b) Khi x= 25 
c) 
 TMĐK 
Vậy x = 2005 thì P.
Dạng 5
Bài 1: Cho biểu thức 
a) Tìm ĐKXĐ, và rút gọn A.
b)Tính giá trị của A khi x=.
c)Tìm giá trị của x để 
Bài giải: a) ĐKXĐ x > 0; x .
=
b) Khi x = 
c)
 Vậy x > 9 thì 
Bài 2: Cho biểu thức: 
a) Tìm ĐKXĐ, rút gọn biểu thức A
b) Tính giá trị của biểu thức A
c) Với giá trị nào của x thì 
Bài giải: a) ĐKXĐ x > 0; x . 
b) Khi x=36 
c) (vì )
 Kết hợp với điều kiện xác định 0 < x <1 thì 
Chuyên đề tam thức bậc hai
 A.lý thuyết
I. áp dụng công thức nghiệm và công thức nghiệm thu gọn để xét số nghiêm phương trình bậc hai.
Cho phương trình bậc hai: ax+bx+c=0(a0)
.Nếu b =2b thì = b- ac
 1. Phương trình có nghiệm khi .
Ta có thể xét hai trường hợp:
+Trường hợp 1: 
Nếu a = 0, b 0 phương trình có nghiệm x=.
+Trường hợp 2 :
 hoặc 
 2.Phương trình có 2 nghiệm phân biệt khi .
 hoặc 
 3.Phương trình có nghiệm kép khi.
 hoặc 
 4. Phương trình vô nghiệm khi.
 hoặc 
Ví dụ1:
Cho phương trình 2x-(4m+3)x+2m-1=0.Với m là tham số,tìm giá trị m để phương trình.
 a.Phương trình có nghiệm
 b.Phương trình có2nghiệm phân biệt
 c.Phương trình có nghiệm kép
 d. Phương trình vô nghiệm
Giải:
=(4m+3)-4.2(2m-1)=24m+17.
 a.Phương trình có nghiệm khi .
 m 
 b.Phương trình có 2 nghiệm phân biệt khi.
 c.Phương trình có nghiệm kép khi.
 d. Phương trình vô nghiệm khi.
Ví du 2 :
Cho phương trình mx-2(m-1)x+(m-4)=0 .Với m là tham số,tìm giá trị m để phương trình.
 a.Phương trình có nghiệm
 b.Phương trình có 2 nghiệm phân biệt
 c.Phương trình có nghiệm kép
 d. Phương trình vô nghiệm
Giải: 
Ta có :a0m,= b-ac=-m(m-4)=m-2m+1-m+4m=2m+1
 a.Phương trình có nghiệm khi . 
+Trường hợp 1: 
Nếu a=0 m=0 ,phương trình có nghiệm x==2.
+Trường hợp 2 :
 b.Phương trình có 2 nghiệm phân biệt khi.
 c.Phương trình có nghiệm kép khi.
 d. Phương trình vô nghiệm khi.
II . Hệ thức vi- ét và ứng dụng.
 1. Hệ thức vi- ét 
Nếu x,xlà hai nghiệm của phương trình ax+bx+c=0(a0) thì x+ x=và x.x=
3.áp dụng để xác định dấu các nghiệm
Cho phương trình ax+bx+c=0(a0)
cú 2 nghiệm: trỏi dấu, cựng dấu, cựng dương, cựng õm .
Ta lập bảng xột dấu sau:
Dấu nghiệm
x1
x2
D
Điều kiện chung
trỏi dấu
P < 0
D ³ 0
D ³ 0 ; P < 0.
cựng dấu,
P > 0
D ³ 0
D ³ 0 ; P > 0
cựng dương,
+
+
S > 0
P > 0
D ³ 0
D ³ 0 ; P > 0 ; S > 0
cựng õm
S < 0
P > 0
D ³ 0
D ³ 0 ; P > 0 ; S < 0.
Ví dụ : 
Cho phương trình x+(2m+2)x+m-4=0
Có hai nghiệm trái dấu 
Có hai nghiệm cùng dấu 
Có hai nghiệm dương
Có hai nghiệm âm
Giải :
= b- 4ac = (2m+2)- 4(m-4) = 4m+ 8m + 4 - 4m-16 = 8m -12
* Có hai nghiệm trái dấu 
 x.x== m- 4 = (m+1)(m-1)<0
-Trường hợp 1. -1< m <1
-Trường hợp 2. m <-1 và 1 < m
 *Có hai nghiệm cùng dấu
m>2
*Có hai nghiệm dương
 m>2
*Có hai nghiệm âm khi 
m>2
4.áp dụng để xác định hai số biết tổng S và P của chủng 
-Nếu hai số x,x sao cho x+x=S, x.x=P thì x,xlà nghiệm phương trình 
x-Sx+P=0 
Ví dụ: 
Tìm hai số, biết tổng của chủng là 15 và tích của chủng là 54.
Giải : 
Nếu hai số phải tìm là x,x sao cho x+x=S =15, x.x=P=54 thì x,xlà nghiệm phương trình 
x-15x+54=0 
=(-15)-4.54=225-216=9;=3
x=; x=
Vậy hai số cần tìm là 9 và 6.
b.Bài tập 
Bài tập 1.
Cho phương trình (m-4)x-2mx+m-2=0,trong đó m là tham số 
a.Giải phương trình khi m=3.
b.Tìm m để phương trình có nghiệm x=.
c.Tìm m để
 -phương trình có nghiệm kép 
 -phương trình có hai nghiệm phân biệt
Giải : 
a.với m=3 ta có -x-6x+1=0
=(-3)+1=10;=
-phương trình có hai nghiệm phân biệt
x=-3- ; x=-3+
b. Phương trình có nghiệm x=,thay vào phương trình ta có 
(m-4)2-2m+m-2=0m=10(3+2)
c.-Phương trình có nghiệm kép khi 
Ta có x= x==
-Phương trình có hai nghiệm phân biệt
Công thức tính nghiệm của phương trình là x= ; x=
Bài tập 2.
Giải và biện luận phương trình
 a.2x - (2-k)x=k(k-2).
 b.(2k-1)x-4kx+1=0.
Giải :
 a.Phương trình đã cho có thể viết 2x-(2-k)x-k(k-2)=0
=(2-k)+8k(k+2)=4-4k+k+8k+16k=9k+12k+4=(3k+2)với mọi k.
Vậy phương trình đã cho luôn có nghiệm với mọi k .
b.- Nếu 2k-1=0 hay k= thì -4kx+1=-2x+1=0,ta có nghiệm x=.
 - Nếu 2k-10 hay k thì ta tìm được =(-2k)-(2k-1)=4k-4k+4k-1=4k-10
 Tức là k ,phương trình có nghiệm.
Vậy với k >và kphương trình có hai nghiệm phân biệt 
x=;x=
 Với k = phương trình có một nghiệm kép x= x=-=
 Với k < thì phương trình vô nghiệm 
 Bài tập 3.
Cho phương trình x+7x-5=0.Không giải phương trình hãy tính .
a.Tổng và tích của hai nghiệm
b.Tổng các nghịch đảo của hai nghiệm
c.Tổng các bình phương của hai nghiệm
d.Bình phương của hiệu hai nghiệm
e.Tổng các lập phương của hai nghiệm 
Giải :
Ta thấy rằng phương trình đã cho luôn có nghiệm vì các hệ số avà c khác dấu.
a.Tổng của hai nghiệm là S=x+x=-7 và tích của hai nghiệm là P= x.x=-5.
b. Tổng các nghịch đảo của hai nghiệm là 
c.Tổng các bình phương của hai nghiệm 
d.Bình phương của hiệu hai nghiệm là 59+10=69.
e.Tổng các lập phương của hai nghiệm là 
Bài tập 4.
Cho phương trình 2x+(2p-1)x+p-1=0
a.Tìm p để phương trình có hai nghiệm phân biệt .
b.Tìm p để cả hai nghiệm đều dương.
c.Tìm một hệ thức không phụ thuộc vào p.
Giải :
a.Phương trình có 2 nghiệm phân biệt khi =(2p-1)- 4.2(p-1)=(2p-3)> 0 p
b.Phương trình có hai nghiệm đều dương ta giải hệ phương trình 
Hệ phương trình vô nghiệm ,không có giá trị nào của p để cả hai nghiệm đều dương.
c. Do S= và P== nên ta có :S+2P=+
Vậy hệ thức giữa hai nghiệm không phụ thuộc vào p là 
Bài tập 5.
Cho phương trình x- mx + m-1=0 với m là tham số .
a.Chứng minh phương trình luôn có nghiệm với mọi m.
b.Gọi x,xlà các nghiệm .Tìm giá trị nhỏ nhất của A= .
Giải . 
a.Ta có ,vậy phương trình luôn có nghiệm với mọi m .
b. A= = +2xx-2xx=(x+x)- 2xx= m-2(m-1)= m-2m+2=
m-2m+1+1=(m-1)+11 mA nhỏ nhất bằng 1 khi (m-1)=0 m=1
Bài tập 6.
Cho phương trình x- 2x + m =0 với m là tham số .
a.Tìm m sao cho phương trình có hai nghiệm phân biệt x,xđều là số dương.
b. Tìm m sao cho phương trình có hai nghiệm phân biệt x,xthỏa mãn :
Giải: 
a.Điều kiện để phương trình có hai nghiệm phân biệt đều dương là :
b.Điều kiện để phương trình có hai nghiệm phân biệt =1-m > 0m<1(1)
Khi đó S=x+x=2 và P= x.x= m nên :
Điều kiện m(2)
Ta có 3(4-2m)=-10m4m=-12m=-3 thỏa mãn (1),(2).
Bài tập 7. 
Cho phương trình x+ 2(m+1)x + m=0 ,với m là tham số .
a.Giải phương trình khi m=2 .
b.Tìm các giá trị của m để phương trình có hai nghiệm phân biệt .
c.Tìm các giá trị của m để phương trình có hai nghiệm phân biệt và trong đó có một nghiệm bằng (-2).
Giải:
a.Khi m=2 thay vào phương trình ,ta có x+ 6x + 4=0
=3-4=5, =
Phương trình có hai nghiệm phân biệt
x= -3+, x=-3-.
b.Phương trình có hai nghiệm phân biệt khi =(m+1)- m=2m+1>0m >
c.Phương trình có hai nghiệm phân biệt và trong đó có một nghiệm bằng (-2).
- Phương trình có hai nghiệm phân biệt khi >0 m >
- Theo hệ thức Vi- ét ta có 
- Theo giá thiết , phương trình có một nghiệm bằng (-2) , giả sử x=-2 .Từ hệ phương trình (1) ta có 
-Từ hệ phương trình (2), rút gọn hai vế ta có m+4m=0m(m+4)=0
Với m=-4 (loại),m=0 (thỏa mãn) điều kiện m >.
Vậy m=0 phương trình có hai nghiệm phân biệt và trong đó có một nghiệm bằng 
(-2).
Bài tập 8.
 Cho phương trình (m+1)x+ 5x + m-1=0 ,với m là tham số .
a.Tìm các giá trị của m để phương trình có hai nghiệm trái dấu.
b.Tìm các giá trị của m để phương trình có hai nghiệm trái dấu và trong hai nghiệm đó có một nghiệm bằng 4.
Giải:
a.Phương trình có hai nghiệm trái dấu khi
b.Phương trình có hai nghiệm trái dấu và trong hai nghiệm đó có một nghiệm bằng 4. 
-áp dụng hệ thức Vi-ét ta có 
Thay giá trị x=4 vào (I) ta có m+16m+35=0 m=-8+;m=-8-
Các giá trị m, mđều thỏa mãn điều kiện m<1 và m-1
Vậy m=-8+;m=-8- phương trình có hai nghiệm trái dấu và trong hai nghiệm đó có một nghiệm bằng 4.
Bài tập 9.
Cho phương trình (m+1)x- 2(m-10x + m-3 =0 ,với m là tham số .
a.Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m khác (-1).
b.Tìm giá trị m để phương trình có hai nghiệm cùng dấu 
c. Tìm giá trị m để phương trình có hai nghiệm cùng dấu và trong hai nghiệm đó có nghiệm này gấp đôi nghiệm kia .
Giải :
a.Phương trình luôn có hai nghiệm phân biệt khi
Vậy phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m -1.
b.-Theo câu a ,ta đã có >0 với mọi giá trị m-1
 -Phương trình có hai nghiệm cùng dấu khi 
Vậy phương trình có hai nghiệm cùng dấu khi m>3 hoặc m<-1
c.Theo câu a ,b phương trình có hai nghiệm cùng dấu khi >0 và ta có m>3 hoặc m<-1.
Mặt khác theo hệ thức Vi-ét ta có :
Với giả thiết cho x=2x,thay vào (I) ta có 
Rút ra ta được : m- 2m- 35 = 0 m=-5 ;m=7 .Với giá trị m ;mđều thỏa mãn điều kiện m >3 và m <-1.
Vậy phương trình có hai nghiệm cùng dấu và nghiệm này gấp đôi nghiệm kia khi m=-5 hoặc m=7.
Bài tập 10.
Cho phương trình m(x-4x+3)+2(x-1)=0
a.Giải phương trình khi m=-.
b. Chứng minh rằng phương trình luôn có nghiệm với mọi giá trị của m .
c.Tìm m để phương trình đã cho có hai nghiệm nguyên.
Giải:
a.Với m=- .Ta có x-8x+7=0
Có a+b+c = 1+(-8)+7 = 0 x=1;x==7.
b.Phương trình đã cho trở thành : mx-2(m-1)x+3m-2=0 (1)
+ Với m=0 ,(1) 2x-2=0 x=1.
+ Với m0 :0 .
 Vậy phương trình luôn có nghiệm với mọi giá trị của m.
c.Ta có m(x-4x+3)+2(x-1)= (x-1) 
Xét phương trình m(x-3)+2 = 0 
Để phương trình có hai nghiệm thì m0 khi mx-3m+2=0x==3-.
Để phương trình có hai nghiệm nguyên thì 2m hay m=1;m=
Bài tập 11.
Cho phương trình x- (m+2)x+2m = 0 (1)
a.Giải phương trình khi m=-1
b.Tìm m để phương trình có hai nghiệm x,xthỏa mãn (x+x)- x.x5.
Giải:
a.Với m=-1 .Ta có x- x-2 = 0 Có a-b+c= 1-(-1)+(-2)=0 x=-1,x=2
b. Ta có: =(m+2)-4.2m=m+ 4m + 4- 8m = m- 4m + 4 = ( m- 2)0 . Vậy phương trình có nghiệm .
Ta có (x+x)- x.x=m+2m+4 5 m+2m+ 1+3 5 m+2m+ 1 5-3
 (m+1) 2 -m+1-1-m-1
Bài tập 12.
Cho phương trình x- px + p-1 = 0 
a.Chứng minh rằng phương trình luôn có nghiệm với mọi giá trị của p .
b.Tính theo p giá trị biểu thức M=x+x- 6x.x.
c.Tìm giá trị nhỏ nhất của M.
Giải:
a.Ta có .Chứng tỏ rằng phương trình luôn có nghiệm với mọi giá trị của p .
b.Ta có M=x+x- 6x.x =(x+x)-2x.x- 6x.x=(x+x)-8x.x
= p- 8(p-1) = p- 8p + 8 = p- 8p + 16 - 8 = (p-4)- 8.
c.M=(p-4)- 8-8,vậy M đạt giá trị nhỏ nhất M=-8 khi (p-4)=0 p-4=0p=4.
Bài tập 13.
Chứng minh rằng nếu các hệ số của hai phương trình bậc hai x+px+q=0 và 
 x+px+ q=0 ,liên hệ với nhau bởi hệ thức pp=2(q+q) thì ít nhất một trong hai phương trình trên có nghịêm.
Giải 
Gọi phương trình x+px+q=0 (1) và x+px+ q=0 (2) 
Ta có =p-4 q;=-4 q;
+= p-4 q+-4 q= p+- 4(q+ q).
Vì 2(q+q)= pp4(q+ q) = 2pp.
Do đó += p+- 4(q+ q)= p+-2pp= 
Điều này chứng tỏ ít nhất một trong hai biệt thức hoặc phải >0 .Vậy ít nhất một trong hai phương trình có nghiệm.
Bài tập 14.
Chứng minh rằng phương trình ax+ bx + c = 0 có nghiệm nếu một trong hai điều kiện sau
a( a + 2b + 4c ) < 0
5a + 3b + 2c = 0
Giải:
Ta có .
a( a + 2b + 4c ) = a+2ab+4ac ( a+b)0
0,phương trình có nghiệm .
b) 5a + 3b + 2c = 0 10a+6ab+4ac=0(3a+b)+ a= b-4ac00,phương trình có nghiệm .
Bài tập 15.
Chứng minh rằng nếu hai phương trình bậc hai x+px+q=0 và x+px+ q=0 có nghiệm chung thì : (q- q)+(p-p)(qp-qp)=0.
Giai:
Hai phương trình có nghiệm chung 
 có nghiệm 
Đặt y=x,ta có 
-Nếu pp,giải hệ phương trình ta có x=và y=.Do y=xsuy ra 
=(),khai triển biến đổi ta có :(q-q)+( q-q)( qp-qp)=0.
-Nếu p=pta có hệ Hệ này có nghiệm ,suy ra q=q.Do đó đẳng thức cần chứng minh có dạng 0 = 0, hiến nhiên đúng.
Chuyên đề:
Giải bài toán bằng cách lập phương trình.
A) tóm tắt lý thuyết
Bước 1: Lập phương trình hoặc hệ ohương trình:
	a) Chọn ẩn và đặt điều kiện cho ẩn.
	b) Biểu diễn các đại lượng chưa biết thông qua ẩn và các địa lượng đã biết.
	c) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Đối chiếu nghiệm của pt, hệ phương trình (nếu có) với điều kiện của ẩn số để trả lời.
	Chú ý: Tuỳ từng bài tập cụ thể mà ta có thể lập phương trình bậc nhất một ẩn, hệ phương trình hay phương trình bậc hai.
	Khi đặt diều kiện cho ẩn ta phải dựa vào nội dung bài toán và những kiến thức thực tế....
B) Các dạng toán
Dạng 1: Toán về quan hệ các số.
	Nững kiến thức cần nhớ: 
+ Biểu diễn số có hai chữ số : 
+ Biểu diễn số có ba chữ số : 
+ Tổng hai số x; y là: x + y
+ Tổng bình phương hai số x, y là: x2 + y2
+ Bình phương của tổng hai số x, y là: (x + y)2.
+ Tổng nghịch đảo hai số x, y là: .
Ví dụ 1: Mộu số của một phân số lớn hơn tử số của nó là 3 đơn vị. Nếu tăng cả tử và mẫu của nó thêm 1 đơn vị thì được một phân số mới bằng phân số đã cho. Tìm phân số đó?
Giải: 
	Gọi tử số của phân số đó là x (đk: )
	Mẫu số của phân số đó là x + 3.
Nếu tăng cả tử và mẫu thêm 1 đơn vị thì
	Tử số là x + 1
	Mẫu số là x + 3 + 1 = x + 4
Được phân số mới bằng ta có phương trình .
Ví dụ 2: Tổng các chữ số của 1 số có hai chữ số là 9. Nếu thêm vào số đó 63 đơn vị thì số thu được cũng viết bằng hai chữ số đó nhưng theo thứ tự ngược lại. Hãy tìm số đó?
	Giải 
Gọi chữ số hàng chục là x (
Vì tổng 2 chữ số là 9 ta có x + y = 9 (1)
Số đó là 
Số viết ngược lại là 
Vì thêm vào số đó 63 đơn vị thì được số viết theo thứ tự ngược lại ta có 
Từ (1) và (2) ta có hệ phương trình 
Vậy số phải tìm là 18.
Ví dụ 3: Tìm hai số tự nhiên liên tiếp có tổng các bình phương của nó là 85.
	Giải 
Gọi số bé là x (). Số tự nhiên kề sau là x + 1.
Vì tổng các bình phương của nó là 85 nên ta có phương trình: x2 + (x + 1)2 = 85
Phương trình có hai nghiệm 
Vậy hai số phải tìm là 6 và 7.
Bài tập: 
Bài 1: Đem một số nhân với 3 rồi trừ đi 7 thì được 50. Hỏi số đó là bao nhiêu?
Bài 2: Tổng hai số bằng 51. Tìm hai số đó biết rằng số thứ nhất thì bằng số thứ hai.
Bài 3: Tìm một số tự nhiên có hai chữ số, biết tổng các chữ số của nó là 7. Nếu đổi chỗ hai chữ số hàng đơn vị và hàng chụccho nhau thì số đó giảm đi 45 đơn vị.
Bài 4: Tìm hai số hơn kém nhau 5 đơn vị và tích của chúng bằng 150.
Bài 5: Tìm số tự nhiên có 2 chữ số, biết rằng số đó bằng lập phương của số tạo bởi chữ số hàng vạn và chữ số hàng nghìn của số đã cho theo thứ tự đó.
Đáp số:
Bài 1: Số đó là 19;
Bài 2: Hai số đó là 15 và 36
Bài 3: Số đó là 61
Bài 4: Hai số đó là 10 và 15 hoặc -10 và -15;
Bài 5: Số đó là 32.
Dạng 2: Toán chuyển động
Những kiến thức cần nhớ:
	Nếu gọi quảng đường là S; Vận tốc là v; thời gian là t thì:
S = v.t; .
Gọi vận tốc thực của ca nô là v1 vận tốc dòng nước là v2 tì vận tốc ca nô khi xuôi dòng nước là 
v = v1 + v2. Vân tốc ca nô khi ngược dòng là v = v1 - v2 
Ví dụ1: Xe máy thứ nhất đi trên quảng đường từ Hà Nội về Thái Bình hết 3 giờ 20 phút. Xe máy thứ hai đi hết 3 giờ 40 phút. Mỗi giờ xe máy thứ nhất đi nhanh hơn xe máy thứ hai 3 km.
Tính vận tốc của mỗi xe máy và quảng đường từ Hà Nội đến Thái Bình?
Giải: 
Gọi vận tốc x thứ nhất là x (km/h), đk: x>3; 
Vận tốc của xe tứ hai là x - 3 (km/h).
Trong 3 giờ 20 phút (=giờ) xe máy thứ nhất đi được 
Trong 3 giờ 40 phút (=giờ) xe máy thứ nhất đi được 
Đó là quảng đường tứ Hà nội đến Thái Bình nên ta có phương trình 
 (thoả mãn điều kiện bài toán).
Vậy vận tốc của xe máy thứ nhất là 33 km/h. Vận tốc của xe máy thứ hai là 30 km/h.
Quảng đường từ Hà Nội đến Thái Bình là 110 km.
Ví dụ 2: Đoạn đường AB dài 180 km . Cùng một lúc xe máy đi từ A và ô tô đi từ B xe máy gặp ô tô tại C cách A 80 km. Nếu xe máy khởi hành sau 54 phút thì chúng gặp nhau tại D cách A là 60 km. Tính vận tốc của ô tô và xe máy ?
	Giải 
Gọi vận tốc của ô tô là x (km/h), đk: x > 0.
Gọi vận tốc của xe máylà y(km/h), đk: y > 0.
Thời gian xe máy đi để gặp ô tô là (giờ)
Quảng đường ô tô đi là 100 km nên thời gian ô tô đi là (giờ)
ta có phương trình (1)
Quảng đường xe máy đi là 60 km nên thời gian xe máy đi là (giờ)
Quảng đường ô tô đi lag 120 km nên thời gian ô tô đi là (giờ)
Vì ô tô đi trước xe máy 54 phút = nên ta có phương trình 
.
Từ (1) và (2) ta có hệ phương trình 
Vậy vận tốc của ô tô là 50 km/h. Vận tốc của xe máy là 40 km/h.
Ví dụ 3: Một ô tô đi trên quảng đường dai 520 km. Khi đi được 240 km thì ô tô tăng vận tốc thêm 10 km/h nữa và đi hết quảng đường còn lại. T ính vận tốc ban đầu của ô tô biết thời gian đi hết quảng đường là 8 giờ.
Giải:
	Gọi vận tốc ban đầu của ô tô là x (km/h), đk: x>0.
Vận tốc lúc sau của ô tô là x+10 (km/h).
Thời gian ô tô đi hết quảng đường đầu là (giờ)
Thời gian ô tô đi hết quảng đường đầu là (giờ)
Vì thời gian ô tô đi hết quảng đường là 8 giờ nên ta có phương trình
Phương trình có hai nghiệm 
Vậy vận tốc ban đầu của ô tô là 60 km/h.
Bài tập: 
1. Một ô tô khởi hành từ A với vận tốc 50 km/h. Qua 1 giờ 15 phút ô tô thứ hai cũng khởi hành từ A đi cùng hướng với ô tô thứ nhất với vận tốc 40 km/h. Hỏi sau mấy giờ thì ô tô gặp nhau, điểm gặp nhau cách A bao nhiêu km?
2. Một ca nô xuôi dòng 50 km rồi ngược dòng 30 km. Biết thời gian đi xuôi dòng lâu hơn thời gian ngược dòng là 30 phút và vận tốc đi xuôi dòng lớn hơn vận tốc đi ngược dòng là 5 km/h.
Tính vận tốc lúc đi xuôi dòng?
	3. Hai ô tô cùng khởi hành cùng một lúc từ A đến B cách nhau 150 km. Biết vận tốc ô tô thứ nhất lớn hơn vận tốc ô tô thứ hai là 10 km/h và ô tô thứ nhất đến B trước ô tô thứ hai là 30 phút. Tính vânl tốc của mỗi ô tô.
	4. Một chiếc thuyền đi trên dòng sông dài 50 km. Tổng thời gian xuôi dòng và ngược dòng là 4 giờ 10 phút. Tính vận tốc thực của thuyền biết rằng một chiếc bè thả nổi phải mất 10 giờ mới xuôi hết dòng sông.
	5. Một người đi xe đạp từ A đến B cách nhau 108 k