Bộ Đề kiểm tra học kỳ I môn: Toán 9

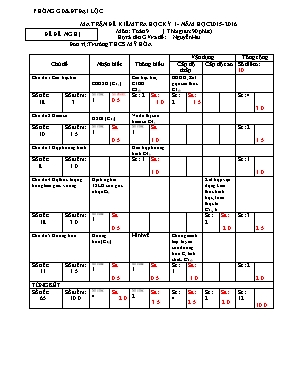
PHÒNG GD&ĐT ĐẠI LỘC
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I - NĂM HỌC 2015- 2016
ĐỀ ĐỀ NGHỊ
 Môn: Toán 9 ( Thời gian: 90 phút)
 Họ và tên GV ra đề: Nguyễn Hai
 Đơn vị: Trường THCS MỸ HÒA
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng cộng
Cấp độ thấp
Cấp độ cao
Số điểm: 10
Chủ đề 1:Căn bậc hai
CBHSH (C1a)
Căn bậc hai, CTBH
C2ab
BDĐG, Rút gọn căn thức C3ab
Số tiết: 
 18
Số điểm: 
 3
Số câu: 1
Số điểm: 0.5
Sc: 2
Sđ: 
 1.0
Sc: 2
Sđ: 
 1.5
Sc: 4
 3.0
Chủ đề 2:Hàm số
HSBI (C1b)
Vẽ đồ thị của hàm số C4a
Số tiết: 
 10
Số điểm: 
 1.5
Số câu: 1
Sđ
 0.5
Số câu: 1
Sđ
 1.0
Sc: 2
 1.5
Chủ đề 3:Hệ phương trình
Giải hệ phương trình C4b
Số tiết: 
 8
Số điểm: 
 1.0
Sc: 1
Sđ:
1.0 
Sc: 1
 1.0
Chủ đề 4 Hệ thức lượng trong tam giác vuông
Định nghĩa TSLG của góc nhọnC1c
Kết hợp vận dụng kiến thức hình học,Toán thực tế
C5c, 6
Số tiết: 
 18
Số điểm: 
 3.0
Số câu: 1
Sđ
 0.5
Sc: 2
Sđ: 
 2.0
Sc: 3
 2.5
Chủ đề 5 Đường tròn
Đường tròn(C1d)
Hình vẽ
Chứng minh tiếp tuyến của đường tròn C, tính chất.. C5ab
Số tiết: 
 11 
Số điểm: 
 1.5
Số câu: 1
Sđ
 0.5
Số câu: 1
Sđ
 0.5
Sc: 1
Sđ: 
 1.0
Sc: 2
 2.0
TỎNG KẾT
Số tiết: 
 65
Số điểm: 
 10.0
Số câu: 4
Sđ 
 2.0
Số câu: 2
Sđ:
 3.5 
Sc: 4
Sđ:
2.5 
Sc: 2
Sđ:
 2.0 
Sc: 12
 10.0
PHÒNG GD&ĐT ĐẠI LỘC
 ĐỀ KIỂM TRA HỌC KỲ I (NĂM HỌC 2015 – 2016 )
ĐỀ ĐỀ NGHỊ
 Môn: Toán 9 ( Thời gian: 90 phút)
 Họ và tên GV ra đề: Nguyễn Hai
 Đơn vị: Trường THCS MỸ HÒA
Câu 1 ( 2 điểm ) :
 a/ Trong các số 25; ( -5 )2; ; , số nào là căn bạc hai số học của 5.
 b/ Trong các hàm số: y = - x + 3 ; y = 3x - 5, hàm số nào đồng biến trên R 
 c/ Tam giác ABC vuông tại A, AB = 3cm, AC = 6cm. Tìm
 d/ Cho đường tròn ( O; 4cm ) và điểm M có OM = 3cm. Cho biết vị trí điểm M vao đường tròn ( O )
Câu 2 ( 1 điểm ) :
 a/ Với giá trị nào của x thì xác định
 b/ Thực hiện phép tính : 
Câu 3 ( 1.5 điểm ) : Cho biểu thức A = với x0 , x1.
 a/ Rút gọn A; 
 b/ Tìm giá trị nguyên của x để A có giá trị nguyên.
Câu 4 ( 2 điểm ) :
 a/ Vẽ đồ thị của hàm số y = –3x + 5
 b/ Giải hệ phương trình: 
Câu5 ( 2.5 điểm ) :
 Cho tam giác nhọn ABC; AB < AC, đường cao AH. Đường tròn tâm O, Đường tròn
 tâm O, đường kính AH cắt AB, AC lần lượt tại M, N.
 a/ Chứng minh BC là tiếp tuyến của đường tròn ( O )
 b/ So sánh AH và MN 
 c/ Đường thẳng MN cắt BC tại S. Chứng minh: SM. SN = SB. SC
Câu 6 ( 1 điểm ) : 
 Một con thuyền qua sông bị nước đẩy nên đi được quảng đường AC tạo với bờ sông
 một góc 520, bề rộng AB của khúc sông là 200m, (hình vẽ dưới). Hỏi con thuyền phải
 đi quảng đường bao nhiêu mới đến bờ bên kia ( làm tròn đến chữ số thập phân thứ nhất)
A
C
B
520
 ---------------Hết----------------
THCS MỸ HOÀ- TỔ TOÁN
 HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HỌC KÌ I MÔN TOÁN 9 . 2015- 2016 . GV : Nguyễn Hai
Câu
Nội dung
Điểm
C1
(2 đ)
C1( 2đ)
Trả lời đúng mỗi ý 0.5
C2( 1đ )
 a/ Với giá trị nào của x thì xác định
 xác định - x + 5 0
0.25
 x 5
0.25
b/ = 
0.25
0.25
C3(1.5đ)
 Cho biểu thức A = với x0 , x1.
a/Biến đổi: A= 
0.50
 A= 
0.25
 A= với x0 , x1.
0.25
b/ A có giá trị nguyên 
0.25
 Giải tìm được x = 0; x= 4
 KL: x=0 hay x = 4
0.25
C3(2đ)
 a) Vẽ đồ thị ( d ) của hàm số y = – 3x + 5
 Tính đúng hai điểm thuộc đồ thị
 Vẽ đúng
0.50
0.50
 b/
0.25
0.25
0.50
C5(2.5đ)
Hình vẽ
0.25
a/ Chứng minh O là trung điểm của AH
 OH là bán kính của ( O )
0.25
0.25
 CH OH tại O, Kết luận
0.25
b/ AH là đường kính của ( O ), MN là dây không qua tâm
0.25
 AH > MN ( Tính chất đường kính là dây lớn nhất )
0.25
c/ Chứng minh AM. AB = AN. AC
0.25
Chứng minh hai tam giác AMN và ACB đồng dạng.
0.25
Chứng minh hai tam giác SMB và SCN đồng dạng.
0.25
Chứng minh: SM. SN = SB. SC
0.25
C5
(1.0 đ )
 Tìm số đo góc BAC bằng 380 
 0.25
 Tam giác ABC vuông tại B  , suy ra: 
0.25
0.25
 Trả lời
0.25
Các bài tập từ đề
Đại số
Bài 1 : (1đ) Tính : 
Bài 2 : (3đ) Cho biểu thức : M = 
Rút gọn M.
Tìm a để M là số nguyên
Bài 3 : (2đ) 
Vẽ đồ thị hàm số y = 2x + 3
Gọi A, B lần lượt là giao điểm của đường y = 2x + 3 và trục Ox, Oy. Tính diện tích tam giác OAB.
Câu1 ( 1điểm)
Tính 
Tìm x để xác định.
Câu 2 ( 2,5điểm) Cho hàm số y = (m-1)x + 2 (1)
Tìm m để hàm số (1) là hàm số đồng biến;
	b) Tìm m để đồ thị hàm số (1) là đường thẳng song song với đường thẳng y = 2x;
Tìm m để đồ thị của hàm số (1) đồng quy với hai đường thẳng
 y-3= 0 và y = x-1
câu 3 (2,5 điểm) Cho biểu thức :P = 
 a) Rút gọn P b) Tìm x để P<1/2
Câu 5( 1điểm) Tìm GTNN của biểu thức 
	 với x > 1
Câu1) 1,5đ
 a) 2+3- 
b) +
c) +
Câu 2) 1,5đ
a)Tìm x : để xác định
b)Tìm x: 2 -12=0
Câu 3) 3đ
Cho hàm số y = (2m-1)x +1 
a)tìm m để hàm số đồng biến 
b)Vẽ đồ thị hàm số khi m = 2
c) Gọi A;B là giao điểm đường thẳng với 2 trục tọa độ . Tính khoảng cách từ O đến AB
Bài 1: (1,5 điểm) Rút gọn các biểu thức sau:
a) A = 	 	
b) B = 	 
c) C =
Bài 2: (1,5 điểm) Cho biểu thức P = ( với x > 0; x ≠ 1)
a) Rút gọn biểu thức P.
b) Tìm giá trị nguyên của x để P nhận giá trị nguyên.
Bài 3: (1,5 điểm) Cho hàm số bậc nhất y = (m - 2)x + 1
a) Tìm m để đồ thị hàm số song song với đường thẳng y = - x - 2014
b) Vẽ đồ thị hàm số với m vừa tìm được.	
Bài 1. (2,5 điểm) Rút gọn các biểu thức sau (Không dùng máy tính) :
a) A = 
b) B = 
c) C = 
Bài 2.(2,0 điểm) 
Vẽ hai đồ thị của hàm số: y = x – 3 và y = − 2x +2 trên cùng mặt phẳng tọa độ. 
Gọi A là giao điểm của hai đường thẳng y = x – 3 và y = − 2x + 2. Tìm tọa độ của điểm A.
Bài 3.(1,0 điểm) Cho tam giác ABC vuông tại A có AH là đường cao và AC = 8cm, AB = 6cm . Tính BH và CH 
Bài 1/
 a. Tìm x để biểu thức xác định.
 b. Rút gọn biểu thức : 
 c. Tính 
 d.Chứng minh đẳng thức : 
 e. Giải phương trình : 
Bài 2/ Cho hàm số y = ax + b
 a. Xác định các hệ số a, b biết đồ thị của hàm số đi qua A(–3 ; 3) và cắt song song đường thẳng y = - 2x.
 b.Với a, b vừa tìm được hãy vẽ đồ thị của hàm số.
 c. Tính góc tạo bởi đường thẳng vừa vẽ với trục Ox.
Bài 1. (1,0 diểm) Tính
 a) ; b) 	
Bài 2: (2,0 điểm) 
Cho biểu thức: +
Rút gọn biểu thức A.
b) Tìm giá trị lớn nhất của A . 	
Bài 3: (2,0đ)
 a)Vẽ đồ thị hàm số y = – x + 2.
 b)Xác định hàm số y = ax + b biết đồ thị hàm số song song với đường thẳng 
 y = – x + 2 và cắt trục hoành tại điểm có hoành độ bằng 3.
Bài 1. (2 diểm) Tính
a) 	b) 	
c) 	d) 
Bài 2. (1 điểm)
a) Tìm x để căn thức sau có nghĩa: .
b) Tìm x biết: 
Bài 3. (2 điểm) Cho hàm số y = (m – 3)x – 3 có đồ thị là (d)
 	a) Tìm m để hàm số trên là hàm số bậc nhất?.
 	b) Tìm m để đồ thị hàm số đã cho tạo với trục Ox một góc tù?
 	c) Tìm m để đồ thị (d) song với đường thẳng (d’): y = 2 + x 
	 	d) Vẽ đồ thị (d) của hàm số trên với m vừa tìm ở câu c.
Bài 4. (1 điểm)
Giải hệ phương trình: 
Bài 1: (2,5 điểm) 	Rút gọn các biểu thức sau
	a) 
 	b) 
 	c) 
 	d) 
Bài 2: (1 điểm) 	Cho hàm số y = 2x - 1 có đồ thị là (D).
a) Hàm số trên đồng biến hay nghịch biến trên R? Vì sao?
b) Tìm giá trị của a để đường thẳng y = ax + 2 song song với đường thẳng (D)
Bài 3: (2 điểm) 	Cho hàm số y = -x + 1 có đồ thị là (D).
Vẽ đồ thị hàm số trên.
Xác định đường thẳng y = 2x + b , biết đường thẳng này đi qua một điểm trên (D) có hoành độ bằng 2
Bài 1.(2 điểm) 
 Rút gọn các biểu thức sau:
a) 2 - + 
b) 
c) () . 
Bài 2. (1 điểm)
a) Tìm x để căn thức có nghĩa.	
b) Tìm x, biết 	
Bài 3.(2,5 điểm)
 Cho hàm số bậc nhất y = - 2x + 6 có đồ thị là đường thẳng (d). 
 a) Hàm số trên đồng biến hay nghịch biến trên R? Vì sao?
 b) Vẽ đồ thị hàm số đã cho.
 c) Xác định đường thẳng y = x + b, biết đường thẳng này đi qua 1 điểm trên (d) có hoành độ bằng 4.
Bài 1.(1,5 điểm) 
Rút gọn các biểu thức sau:
 a) 
 b) 	
 c) 
Bài 2. (1,5 điểm) 	
 a) Tìm x để căn thức có nghĩa.
 b) Tìm x, biết .
Bài 3.(3,0 điểm) Cho hàm số . 
 a) Hàm số trên đồng biến hay nghịch biến trên ?
 b) Vẽ đồ thị của hàm số đã cho.
 c) Gọi A và B là giao điểm của đồ thị hàm số với các trục tọa độ. Tính khoảng cách từ gốc tọa độ O đến đường thẳng AB.
Bài 1: (1,5 điểm) Tính:
a/ 
b/ 
 Bài 2: (1,5đ) Rút gọn biểu thức 
Bài 3: (1đ) Xác định hệ số a của hàm số biết đồ thị hàm số song song với đường thẳng .
Bài 4: (1,5đ) Cho hàm số y = ax+4
Xác định hệ số a của hàm số biết rằng đồ thị hàm số đi qua điểm A(1;2)
Vẽ đồ thị hàm số với a vừa tìm được.
Câu 1: Tính và rút gọn:
a) 
b) 
c) 
Câu 2: a) Tìm x để A = có nghĩa.
Giải phương trình 
Câu 3: Cho hàm số y = x – 3 có đồ thị là (d).
Hàm số trên đồng biến hay nghịch biến trên R.
Vẽ đồ thị (d) của hàm số trên mặt phẳng tọa độ.
Tìm k để điểm A(-1; k) thuộc đồ thị của hàm số.
Xác định giá trị của m để đường thẳng y = (m – 2)x + 1 song song với đường thẳng (d).
Bài 1 :(1điểm) Thực hiện phép tính :
 - 	b) 
Bài 2 :(0 ,5điểm) Tìm x để căn thức sau có nghĩa: 
Bài 3 : (0,5 điểm) Tìm x, biết : 3 - 5 +7 = 28 
Bài 4: (0,5 điểm) Giải hệ phương trình (không dung máy tính cầm tay): 
Bài 5: (1điểm) Cho biểu thức 
Rút gọn biểu thức Q với x > 0 và x ¹ 1 .
Tính giá trị của Q khi x = 3 + 2
Bài 6: (2,5 điểm) 
a) Vẽ đồ thị của các hàm số y = x + 3 và y = - x + 3 trên cùng một mặt phẳng tọa độ
b) Hai đường thẳng y = x + 3 và y = - x + 3 cắt nhau tai C và cắt trục Ox theo thứ tự tại A và B. Tìm tọa độ của các điểm A, B, C?
c) Tính chu vi và diện tích của tam giác ABC. Biết rằng đơn vị đo trên các trục tọa độ là xentimet?
Câu 4: Cho đường tròn tâm O, đường kính AB = 2R, trên đường tròn lấy điểm H sao cho BH = R ; BH cắt tiếp tuyến tại A của đường tròn ở C.
 a/ Chúng minh: AC 2 = HC. BC. Tính AB, BC theo R.
 b/ Gọi I là trung điểm của AH. OI cắt AH tại E. Chứng minh EH là tiếp tuyến của ( O )
 c/ Vẽ HK vuông góc với AB tại K. BE cắt HK tại M. Chứng minh MH = MK.
Bài 5 (3 điểm) Cho đường tròn tâm O, đường kính AB và tiếp tuyến By. Gọi M là một điểm trên đường tròn (O). Tiếp tuyến tại M của đường tròn (O) cắt By tại D. Chứng minh rằng :
Bốn điểm B, D, M, O cùng nằm trên một đường tròn. 
AM // OD
Từ M kẻ MH vuông góc với AB tại H, tính độ dài các cạnh của tam giác ABM; biết MH = 5cm, AH = 3cm. 
Câu 3.(1,5 điểm)
Cho tam giác ABC vuông tại A, AH BC tại H, BH = 9cm, HC = 16cm.Tính AH, AB, AC.
Câu 4.(4,0 điểm)
 Cho đường tròn (O; R) đường kính AB = 10 cm. Tiếp tuyến Bx.Gọi C là một điểm thuộc đường tròn sao cho . Tia AC cắt Bx ở E.
Chứng minh: BC2 = AC. CE.
Tính BE?
Gọi I là trung điểm của BE Chứng minh CI là tiếp tuyến của đường tròn tâm O.
Baì 4 ( 3,0đ )
Cho tam giác ABC vuông tại A , có AB = 15cm ; AC = 20cm .
Tính tanB ; tanC ; so sánh và 
Giải tam giác vuông ABC ( số đo góc làm tròn đến độ ) 
Tính độ dài đường cao AH của tam giác ABC. 
Kẻ HD AB ; HE AC ( DAB ; E AC ) Chứng minh : AD.AB = AE .AC
Bài 5. (2,0 đ)
 Cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đường tròn. Tiếp tuyến tại M và B của nửa đường tròn (O) cắt nhau ở D. Qua O kẻ đường thẳng song song với MB, cắt tiếp tuyến tại M ở C và cắt tiếp tuyến tại B ở N.
 a) Chứng minh : .
 b) Chứng minh rằng AC là tiếp tuyến của nửa đường tròn (O). 
Bài 4 : (4đ)
Cho nửa đường tròn (O ;6cm) đường kính AB và điểm C thuộc nửa đường tròn. Tiếp tuyến tai B và C của nửa đuường tròn cắt nhau ở D. Đường thẳng đi qua O và vuông góc với OD cắt DC ở M.
Tính CD biết CM = 4cm.
Chứng minh OD2 = DB.DM.
Chứng minh MA là tiếp tuyến của nửa đường tròn (O).
Câu 4 ( 3điểm) 
	Cho đường tròn (O) đường kính AB, E thuộc đoạn AO ( E khác A,O và 
AE >EO). Gọi H là trung điểm của AE, kẻ dây CD vuông góc với AE tại H
Tính góc ACB;
Tứ giác ACED là hình gì, chứng minh?
	c) Gọi I là giao điểm của DE và BC. Chứng minh HI là tiếp tuyến của đường tròn đường kính EB.
Bài 5. (2,0 đ)
 Cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đường tròn. Tiếp tuyến tại M và B của nửa đường tròn (O) cắt nhau ở D. Qua O kẻ đường thẳng song song với MB, cắt tiếp tuyến tại M ở C và cắt tiếp tuyến tại B ở N.
 a) Chứng minh : .
 b) Chứng minh rằng AC là tiếp tuyến của nửa đường tròn (O). 
Bài 4: (4,0 điểm) Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng chứa nửa đường tròn này dựng các tia Ax, By vuông góc với AB. Một điểm M di động trên nửa đường tròn (M ≠ A; M ≠ B), tiếp tuyến của nửa đường tròn tại điểm M cắt Ax, By lần lượt tại C, D.
a) Chứng minh DAMB vuông.
b) Chứng minh hệ thức: CD.OM = OC.OD
c) Xác định vị trí của điểm M để diện tích tứ giác ABDC là nhỏ nhất.
Bài 5. (3 điểm)
 Cho nửa đường trịn (O) đường kính AB. Điểm M di chuyển trên nửa đường trịn. Tiếp tuyến tại M và B của nửa đường trịn (O) cắt nhau ở D. Qua O kẻ đường thẳng song song với MB, cắt tiếp tuyến tại M ở C và cắt tiếp tuyến tại B ở N.
 a) Chứng minh rằng tam giác CDN là tam giác cân.
 b) Chứng minh rằng AC là tiếp tuyến của nửa đường tròn (O). 
Bài 3/Cho tam giác ABC vuông tại A có AB = 12 cm, AC = 16 cm.Kẻ đường cao AH
a. Tính AH, BH.
b. Chứng minh rằng : AB.cos B + AC.cos C = 20 
Bài 4/ Cho nửa ( O; R) đường kính AB, qua K là trung điểm OB vẽ đường thẳng vuông góc AB cắt nửa (O, R) tại M.
Tính MK theo R
BM cắt đường thẳng qua O và vuông góc AB tại C; CA cắt đường tròn tại P, AM cắt OC tại I. Chứng minh : B, I, P thẳng hàng.
C/m 4 điểm C, P, I, M cùng nằm trên một đường tròn, xác đinh tâm H của đường tròn này
C/m OM là tiếp tuyến của đường tròn đường kính IC
Bài 5 (4 điểm)
	Cho đường tròn (O;R) và điểm M nằm ngoài đường tròn sao cho OM = 2R.
Qua M vẽ hai tiếp tuyến MB, MC và cát tuyến MAB(A nằm giữa M và B). Gọi I là giao điểm của CD và BM
Chứng minh DC vuông góc với AB. 
Tính OI và CD theo R .
Chứng minh tứ giác MCBD là hình thoi.
Chứng minh rằng đường thẳng MC là tiếp tuyến của đường tròn (B;BI) 	
Bài 4: (1 điểm) 	Cho tam giác ABC có ; đường cao AH, biết AB = 3cm; AC = cm. 
a) Tính số đo 
b) Tính độ dài AH.
Bài 5: (3,5 điểm) 
	Cho đường tròn (O; R) đường kính AB và một đường thẳng (d) tiếp xúc với đường tròn tại A. Từ một điểm C bất kỳ trên (d) kẻ tiếp tuyến CD với đường tròn (O) (điểm D là tiếp điểm).
Chứng minh OC AD.
Đường thẳng BD cắt đường thẳng (d) tại E. Chứng minh CE = CA.
Tính bán kính đường tròn ngoại tiếp tam giác ADE theo R, biết BD = .	
Ở hình vẽ bên, tam giác ABC vuông ở A, đường cao AH. Biết BH = 2cm, CH = 8cm. Tính AH; AB ?
Bài 5.(3,5 điểm) 
Cho tam giác ABC vuông ở A đường cao AH. Gọi D là điểm nằm giữa A và C. Kẻ AE BD tại E.
Chứng minh: Bốn điểm A, B, H, E cùng thuộc một đường tròn. Xác định tâm và bán kính đường tròn này.
Chứng minh: CA là tiếp tuyến của đường tròn đường kính AB.
Chứng minh: BE.BD = BH.BC
Bài 5. (3,5 điểm)
 Cho đường tròn tâm O, bán kính OA= 6cm. Gọi H là trung điểm của OA, đường thẳng vuông góc với OA tại H cắt đường tròn (O) tại B và C. Kẻ tiếp tuyến với đường tròn (O) tại B cắt đường thẳng OA tại M. 
Tứ giác OBAC là hình gì? Vì sao?
Tính độ dài BM.
Chứng minh MC là tiếp tuyến của đường tròn (O).
Bài 4.(4,0 điểm)
 Cho tam giác ABC vuông tại A, đường cao AH. Độ dài của các cạnh AB, AC lần lượt bằng 3cm, 4 cm. 
 a) Tính độ dài của AH, BH, CH.
 b) Vẽ đường tròn (B; 3cm). Chứng minh AC là tiếp tuyến của đường tròn.
 c) Đường phân giác trong của góc A cắt BC tại D. Tính độ dài của HD.
Bài 8: (1điểm) §Ó ®o chiÒu cao cña mét th¸p, mét nhãm häc sinh líp 9 ®Æt gi¸c kÕ th¼ng ®øng c¸ch tim cña ch©n th¸p 100 mÐt vµ quay thanh gi¸c kÕ ®Ó ng¾m nh×n thÊy ®Ønh cña th¸p. C¸c b¹n ®äc trªn gi¸c kÕ ®­îc gãc nh×n so víi chiÒu n»m ngang. BiÕt gi¸c kÕ cã chiÒu cao lµ mÐt. TÝnh chiÒu cao cña th¸p (lµm trßn ®Õn ®Ò-xi-mÐt).
Câu 5 (2,5 điểm)
	Cho hình vuông ABCD cạnh a, lấy điểm M bất kỳ trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với đường thẳng DM tại H, kéo dài BH cắt đường thẳng DC tại K.
1. Chứng minh : BHCD là tứ giác nội tiếp.
2. Chứng minh : KM ^ DB.