Bài tập về giao tuyến của hai mặt phẳng trong không gian

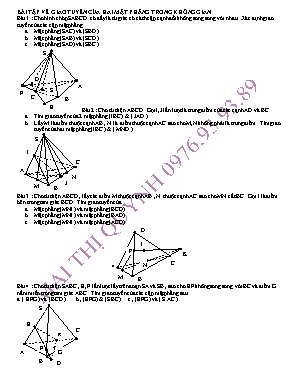
BÀI TẬP VỀ GIAO TUYẾN CỦA HAI MẶT PHẲNG TRONG KHÔNG GIAN 
Bài 1 : Cho hình chóp SABCD có đấy là tứ giác có cách cặp cạnh đối không song song với nhau . Xác định giao tuyến của các cặp mặt phẳng 
Mặt phẳng (SAC) và (SBD ) 
Mặt phẳng (SAB) và (SCD ) 
Mặt phẳng (SAD) và (SBC ) 
D
S
C
E
B
A
S
F
Bài 2 : Cho tứ diện ABCD . Gọi I,J lần lượt là trung điểm của các cạnh AD và BC 
Tìm giao tuyến của 2 mặt phẳng (IBC ) & ( JAD ) 
Lấy M là điểm thuộc cạnh AB , N là điểm thuộc cạnh AC sao cho M,N không phải là trung điểm . Tìm giao tuyến của hai mặt phẳng (IBC ) & ( MND ) 
A
M
B
J
N
C
S
I
Bài 3 : Cho tứ diện ABCD , lấy các điểm M thuộc cạnh AB , N thuộc cạnh AC sao cho MN cắt BC . Gọi I là điểm bên trong tam giác BCD . Tìm giao tuyến của 
Mặt phẳng (MNI ) và mặt phẳng (BCD) 
Mặt phẳng (MNI ) và mặt phẳng (BAD) 
Mặt phẳng (MNI ) và mặt phẳng (ACD) 
 N
K
C
B
M
A
P
I
D
Bài 4 : Cho tứ diện SABC , E, F lần lượt lấy trên đoạn SA và SB , sao cho EF không song song với BC và điểm G nằm miền trong tam giác ABC . Tìm giao tuyến của các cặp mặt phẳng sau 
a. ( EFG ) và (BCD ) b , (EFG) & (S BC) c , (EFG ) và ( S AC ) 
G
F
E
A
K
D
C
S
B
Bài 5 : Cho tứ diện ABCD điểm M , N lần lượt thuộc AB và CD và G là điểm nằm trong tam giác BCD , giả sử không có cặp đường thẳng nào // với nhau . Tìm giao tuyến của cặp
 a. (MCD) và (NAB) b, (GMN ) và (ACD) 
F
M
B
A
E
G
C
N
D
K
Bài 6 : Cho hình chóp SABCD . Hai điểm G và H lần lượt là trọng tâm của hai tam giác SAB &SCD . Tìm giao tuyến của các cặp mặt phẳng sau 
a. (SGH ) & ( ABCD ) b ) ( SGH ) & (SAC ) c ) ( BHG ) & ( SDA ) ;d ) ( BGH ) & (SCD ) 
G
A
N
B
C
M
H
D
S
Bài 7 : Cho hình chóp SABCD có đáy là hình thang ABCD (AB//CD ) . Gọi I là giao điểm của AD và BC . Lấy điểm M thuộc cạnh SC . Tìm giao tuyến của 
Mặt phẳng (SAC ) & ( SBD ) 
Mặt phẳng (SAD ) & ( SBC ) 
Mặt phẳng (DAM ) & ( SBC ) 
Mặt phẳng (DAM) và (SAD) 
 M
A
D
I
C
B
N
S
Bài 8 :Cho hình chóp S.ABCD. Đáy có các cặp cạnh đối không song song. Tìm giao tuyến của
a) (SAC) và (SBD)	b) (SAB) và (SCD)	c) (SAD) và (SBC)
Bài 9 Cho tứ diện ABCD có I, J lần lượt là trung điểm AC, BC; K thuộc BD sao cho KD < KB. Tìm giao tuyến của
a) (IJK) và (ACD)	b) (IJK) và (ABD)
Bài 10. Cho chóp S.ABCD có đáy là hình bình hành. Gọi M, N là trung điểm SB, SD; P thuộc SC: PC < PS. Tìm giao tuyến của:
a) (SAC) và (SBD)	b) (MNP) và (SBD)	c) (MNP) và (SAC)
d) (MNP) và (SAB)	e) (MNP) và (SAD)	f) (MNP) và (ABCD)
Bài 11 Cho chóp S.ABCD có đáy là hình thang, AD là đáy lớn. Gọi M, N là trung điểm BC, CD. Tìm giao tuyến của
a) (SAC) và (SBD)	b) (SMN) và (SAD)	c) (SAB) và (SCD)
d) (SMN) và (SAC)	e) (SMN) và (SAB)
Bài 12. Cho chóp S.ABCD có đáy là hình bình hành. Gọi I, J, K là trung điểm của BC, CD, SA. Tìm giao tuyến của
a) (IJK) và (SAB)	 ;b) (IJK) và (SAD)	c) (IJK) và (SBC)
d) (IJK) và (SBD)
Bài 13 :Cho tứ diện SABC lấy ; MI không // với BC , NI không // với AS . Tìm giao tuyến của mp ( MNI ) với các mặt phẳng (ABC ) và ( SAB ) 
Bài 14 : Cho tứ diện ABCD , M là điểm nằm bên trong tam giác ABD ,N là một điểm nằm bên trong tam giác ADC .Tìm giao tuyến của các cặp mặt phẳng sau 
a, (AMN ) & ( BCD ) b ) (MND ) & (ABC ) 
Bài 15 : Cho hình chóp SABC . Gọi D, E, F lần lượt là trung điểm của AB , BC, SA 
a, Tìm giao tuyến SH của ( SCD ) & ( S AE ) 
b, Tìm giao tnuyến CI của ( SCD ) & (BFC )