Bài tập trắc nghiệm Giải tích 12 - Tính tiến đồ thị - Nguyễn Vũ Minh

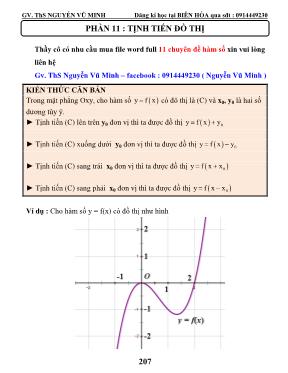
GV. ThS NGUYỄN VŨ MINH Đăng kí học tại BIÊN HÒA qua sđt : 0914449230 
Thầy cô có nhu cầu mua file word full 11 chuyên đề hàm số xin vui lòng 
liên hệ 
Gv. ThS Nguyễn Vũ Minh – facebook : 0914449230 ( Nguyễn Vũ Minh ) 
KIẾN THỨC CĂN BẢN 
Trong mặt phẳng Oxy, cho hàm số ( )y f x= có đô thị là (C) và x0, y0 là hai số 
dương tùy ý. 
► Tịnh tiến (C) lên trên y0 đơn vị thì ta được đồ thị ( ) 0y f x y= + 
► Tịnh tiến (C) xuống dưới y0 đơn vị thì ta được đồ thị ( ) 0y f x y= − 
► Tịnh tiến (C) sang trái x0 đơn vị thì ta được đồ thị ( )0y f x x= + 
► Tịnh tiến (C) sang phải x0 đơn vị thì ta được đồ thị ( )0y f x x= − 
Ví dụ : Cho hàm số y = f(x) có đồ thị như hình 
PHẦN 11 : TỊNH TIẾN ĐỒ THỊ 
207 
GV. ThS NGUYỄN VŨ MINH Đăng kí học tại BIÊN HÒA qua sđt : 0914449230 
► Thì đồ thị hàm số y = f(x) + 1 ( lên trên 1 đơn vị ) 
► Thì đồ thị hàm số y = f(x) - 1 ( xuống dưới 1 đơn vị ) 
y = f(x)+1 
y = f(x) -1 
208 
GV. ThS NGUYỄN VŨ MINH Đăng kí học tại BIÊN HÒA qua sđt : 0914449230 
► Thì đồ thị hàm số y = f(x - 1) ( sang phải 1 đơn vị ) 
► Thì đồ thị hàm số y = f(x + 1) ( sang trái 1 đơn vị ) 
y = f(x + 1) 
y = f(x - 1) 
209 
GV. ThS NGUYỄN VŨ MINH Đăng kí học tại BIÊN HÒA qua sđt : 0914449230 
BÀI TẬP TRẮC NGHIỆM PHẦN 11 
Câu 1 : Cho đường cong (C) có phương trình : 3y x= . Tịnh tiến (C) lên trên 2 
đơn vị thì ta được đồ thị của hàm số nào sau đây ? 
A. 3y x 1= + B. 3y x 2= + 
C. ( )3 y x 2= + D. ( )3 y x 2 2= + +
Câu 2 : Cho đường cong (C) có phương trình : 3y x 2= + . Tịnh tiến (C) sang 
trái 3 đơn vị thì ta được đồ thị của hàm số nào sau đây ? 
A. ( )3y x 3 2= + + B. ( )3y x 3 2= − + 
C. ( )3 y x 3= − D. ( )3 y 1 x 3+ = +
Câu 3 : Cho đường cong (C) có phương trình : 2y x= . Tịnh tiến (C) lên trên 5 
đơn vị, sau đó tịnh tiến đồ thị nhận được sang trái 1 đơn vị thì ta nhận được đồ 
thị của hàm số nào sau đây ? 
A. 2y x 2x 6= + + B. ( )2y x 1 2= − + 
C. ( )2 y x 2 5= + + D. ( )2 y x 2 4= − −
Câu 4 : Cho đường cong (C) có phương trình : ( ) 2x 1y f x
x 3
+
= =
−
 . Tịnh tiến 
(C) sang trái 3 đơn vị sau đó tịnh tiến xuống dưới 2 đơn vị thì ta được đồ thị 
hàm số nào sau đây ? 
A. ( )2 x 3 1y
x 2
+ +
=
−
 B. ( )x 3 1y
3x 2
+ +
=
−
C. 7 y
x
= D. 7 y
2x
=
Câu 5 : Cho đường cong (C) có phương trình : ( )y f x= . Tịnh tiến (C) sang 
trái 1 đơn vị ta được đồ thị hàm số 
210 
GV. ThS NGUYỄN VŨ MINH Đăng kí học tại BIÊN HÒA qua sđt : 0914449230 
A. ( )y f x 1= − B. ( )y f x 1= + 
C. ( )y f x 1= + D. ( )y f x 1= −
Câu 6 : Cho đường cong (C) có phương trình : ( )y f x= . Tịnh tiến (C) sang 
phải 3 đơn vị ta được đồ thị hàm số 
A. ( )y f x 3= − B. ( )y f x 3= + 
C. ( )y f x 3= + D. ( )y f x 3= −
Câu 7 : Cho đường cong (C) có phương trình : ( )y f x= . Tịnh tiến (C) lên trên 
4 đơn vị ta được đồ thị hàm số 
A. ( )y f x 3 4= − + B. ( )y f x 3 4= + + 
C. ( )y f x 3= − D. ( )y f x 4= +
Câu 8 : Cho đường cong (C) có phương trình : ( )y f x= . Tịnh tiến (C) xuống 
dưới 4 đơn vị ta được đồ thị hàm số 
A. ( )y f x 4= − B. ( )y f x 3 4= + + 
C. ( )y f x 4= − D. ( )y f x 4= +
Câu 9 : Cho đường cong (C) có phương trình : ( )y f x= . Tịnh tiến (C) xuống 
dưới 4 đơn vị sau đó tịnh tiến lên trên 2 đơn vị ta được đồ thị hàm số 
A. ( )y f x 4= − B. ( )y f x 3 2= + + 
C. ( )y f x 4= − D. ( )y f x 2= +
Câu 10 : Cho đường cong (C) có phương trình : ( )y f x= . Tịnh tiến (C) xuống 
dưới 4 đơn vị sau đó tịnh tiến sang trái 2 đơn vị ta được đồ thị hàm số 
A. ( )y f x 4= − B. ( )y f x 2 4= + − 
C. ( )y f x 4= − D. ( )y f x 2 4= + + 
211 
GV. ThS NGUYỄN VŨ MINH Đăng kí học tại BIÊN HÒA qua sđt : 0914449230 
Câu 11 : Hàm số ( )y f x= liên tục và đồng biến trên ( )1;2− thì hàm số 
( )y f x 2= + đồng biến trên 
A. ( )1;2− B. ( )1;4 
C. ( )3;0− D. ( )2;4− 
Câu 12 : Hàm số ( )y f x= liên tục và nghịch biến trên ( )0;2 thì hàm số 
( )y f x 3= − nghịch biến trên 
A. ( )3; 1− − B. ( )3;4 
C. ( )3;0− D. ( )3;5 
212