Bài tập tổng hợp học kì 1- Đại số 11 - Nguyễn Quốc Tuấn

Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
1 
CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 
Bài 1. CÁC HÀM SỐ LƯỢNG GIÁC 
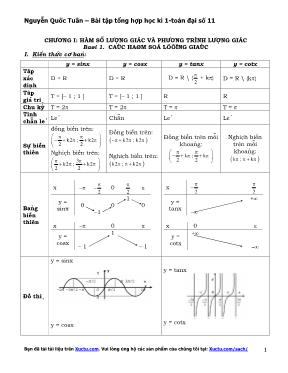
I. Kiến thức cơ bản: 
 y = sinx y = cosx y = tanx y = cotx 
Tập 
xác 
đi ̣nh 
D = R D = R D = R \ {
2

 + k} D = R \ {k} 
Tập 
gia ́ trị 
T = [– 1 ; 1 ] T = [– 1 ; 1 ] R R 
Chu ky ̀ T = 2 T = 2 T =  T =  
Tính 
chă ̃n le ̉ 
Le ̉ Chă ̃n Le ̉ Le ̉ 
Sự biến 
thiên 
đơ ̀ng biến trên: 
k2 ; k2
2 2
  
     
 
Nghi ̣ch biê ́n trên: 
3
k2 ; k2
2 2
  
    
 
Đờng biê ́n trên: 
 k2 ; k2   
Nghi ̣ch biê ́n trên: 
 k2 ; k2   
Đờng biê ́n trên mơ ̃i 
khoa ̉ng: 
k ; k
2 2
  
     
 
Nghi ̣ch biê ́n 
trên mơ ̃i 
khoa ̉ng: 
 k ; k   
Bảng 
biê ́n 
thiên 
x – 
2

 0 
2

  
y = 
sinx 
0 
–1 
0 
1 
0 
x – 0  
y = 
cosx 
– 1 
1 
– 1 
a 
x 
2

 
2

y = 
tanx 
– 
 + 
x 0  
y = 
cotx 
+ 
– 
a 
Đờ thi ̣ 
y = sinx 
y = cosx 
y = tanx 
y = cotx 
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
2 
Bài tâ ̣p ứng dụng: Gia ́o viên cho hs ơn tập hoặc cho hs làm kiê ̉m tra tu ̀y theo mức đơ ̣ 
cu ̉a hs 
1. Hãy xác đi ̣nh giá trị cu ̉a x trên đọan 
3
;
2
 
 
 
 đê ̉ ha ̀m sớ y = sinx : 
a) Nhâ ̣n gia ́ trị bă ̀ng 0. b)Nhận giá trị bă ̀ng 1. 
c) Nhâ ̣n gia ́ trị dương d) Nhận giá trị âm. 
2. Hãy xác đi ̣nh giá trị cu ̉a x trên đọan 
3
;
2
 
 
 
 đê ̉ ha ̀m sớ y = cosx 
a) Nhận gia ́ trị bă ̀ng 0. b) Nhận giá trị bă ̀ng -1. 
c) Nhâ ̣n giá trị dương d) Nhận giá trị âm. 
3. Tìm tập xa ́c định của mỡi ha ̀m sơ ́ sau: 
a) y = 3- sinx b) y = 
1- cosx
sinx
 c) y = 
1-sinx
1+ cosx
 d) y = 
π
tan 2x +
3
 
 
 
e) y =  0tan x - 30 f) y =  0cot x + 60 g) y = sin3x h) y = cos x
2
i) y = cos x j) y = sin
1+ x
1- x
 k) y = 
3
2cosx
 l) y = 
cotx
cosx -1
 m) 
2 1
sin
x
y
x x

 n) y = tan
π
2x -
4
 
 
 
 o) y = cos
2x
x -1
 p) y = tan
x
3
 q) 
tan
tan 1
x
y
x


 r) 
21
sin
x
y
x

 
4. Xét tính chă ̃n, lẻ cu ̉a mỡi hàm sơ ́ sau: 
a) y = x – sinx b) y = 3sinx – 2 c)y = sinx – cosx d) y = sinxcosx + 
tanx e) y = 
cos x
x
 f) y = 1- cosx g) y = 
1+ cosx
1- cosx
 h) 2cos3 4y x  
i) y = x3sin2x j) y = tan x
5
 
 
 
k) y = cos3x l)  2sin 3y x  m) 2 2tan cot 2sin cosy x x x x   
5. Tìm giá trị lớn nhâ ́t va ̀ giá trị nho ̉ nhâ ́t cu ̉a mỡi hàm sơ ́ sau: 
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
3 
Chú ý 1 sin 1x   , 1 cos 1x   và 20 sin 1x  , 20 cos 1x  
sin 2
sin .cos
2
x
x x  
 
2 22sin .cos sin 22 2sin .cos
4 4
x x x
x x   
a) y = 2cos x
3
 
 
 
+ 3 b) y = 21- sin(x ) -1 c) y = 4sin x 
d) y = 2 cosx +1 e) y = 3 – 2sinx f) y = 2(1+ cosx) +1 
g) y = 3sin x
6
 
 
 
 – 2 h) y = 2 + 3cosx i) y = 3 – 4sin2xcos2x 
j) y = cosx + cos x
3
 
 
 
 k) y = cos2x + 2cos2x l) y = 2 25 - 2cos xsin x 
m) y = 3 – 4sinx n) y = 2 – cosx o) 2cos 3
3
y x
 
  
 
 p) sin 2
3
y x
 
  
 
6. Trong mỡi khẳng định sau, khă ̉ng định na ̀o đu ́ng? Khă ̉ng định na ̀o sai? Gia ̉i 
thích vì sao? 
a) Trên mơ ̃i khoảng ma ̀ ha ̀m sớ y = sinx đờng biê ́n thì ha ̀m sơ ́ y = cosx nghịch 
biê ́n. 
b) Trên mơ ̃i khoảng ma ̀ ha ̀m sớ y = sin2x đơ ̀ng biến thì ha ̀m sơ ́ y = cos2x nghịch 
biê ́n. 
CƠNG THỨC LƯỢNG GIÁC 
I. Hê ̣ thức cơ bản 
II. Cơng thức góc liên quan: 
1. Góc đơ ́i a va ̀ a 2. Góc bu ̀ a va ̀ a  3. Góc hơn  : a va ̀ a  4. Go ́c 
phu ̣ nhau: a và 
2
a

 
cos( ) cos
sin( ) sin
tan( ) tan
cot( ) cot
a a
a a
a a
a a
 
  
  
  
sin( ) sin
cos( ) cos
tan( ) tan
cot( ) cot
a a
a a
a a
a a




 
  
  
  
sin( ) sin
cos( ) cos
tan( ) tan
cot( ) cot
a a
a a
a a
a a




  
  
 
 
sin( ) cos
2
cos( ) sin
2
a a
a a


 
 
tan( ) cot
2
cot( ) tan
2
a a
a a


 
 
2 2sin cos 1
tan .cot 1,
2
sin
tan
cos
cos
x x
x x x k
x
x
x
x

 
 

2
2
2
2
1
tan
cos
1
cot
sin
x
x
x
x


sin( 2 ) sin , 1 sin 1
cos( 2 ) cos , 1 cos 1
tan( ) tan ,
2
cot( ) cot ,
x k x x
x k x x
x k x x k
x k x x k



 
 
    
    
   
  
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
4 
5.Góc hơn 
2

: a va ̀ 
2
a

 III. Cơng thức lượng gia ́c 
 1. Cơng thức cợng 2. 
Cơng thức nhân đơi 
3. Cơng thức tích thành tổng 4. Cơng thức tổng 
thành tích 
5. Cơng thức nhân ba 6. Cơng thức ha ̣ bâ ̣c 
7. Cơng thức ti ́nh theo sinx , cosx , tanx theo t = tan
2
x
 8. Các hê ̣ thức câ ̀n 
nhớ: 
8. Đặc biê ̣t 
cos( ) cos cos sin sin
cos( ) cos cos sin sin
sin( ) sin cos cos sin
sin( ) sin cos cos sin
tan tan
tan( )
1 tan tan
tan tan
tan( )
1 tan tan
a b a b a b
a b a b a b
a b a b a b
a b a b a b
a b
a b
a b
a b
a b
a b
  
  
  
  

 


 

2 2
2 2
2
cos 2 cos sin
2cos 1 1 2sin
sin 2 2sin cos
sin 2sin cos
2 2
2 tan
tan 2
1 tan
x x x
x x
x x x
x x
x
x
x
x
 
   




3
3
sin 3 3sin 4sin
cos3 4cos 3cos
x x x
x x x
 
 
 2
2
1 cos 2
cos
2
1 cos 2
sin
2
x
x
x
x




3
3
3sin sin 3
sin
4
3cos cos3
cos
4
x x
x
x x
x




2
2 2 2
2t 1- t 2t
sinx = , cosx = , tanx = 
1+ t 1+ t 1- t
4 4 2 2 2
6 6 2 2 2
1
sin cos 1 2sin cos 1 sin 2
2
3
sin cos 1 3sin cos 1 sin 2
4
x x x x x
x x x x x
    
    
sin( ) cos
2
cos( ) sin
2
tan( ) cot
2
cot( ) tan
2
a a
a a
a a
a a




 
  
  
  
 
 
 
1
cos .cos cos( ) cos( )
2
1
sin .sin cos( ) cos( )
2
1
sin .cos sin( ) sin( )
2
a b a b a b
a b a b a b
a b a b a b
   
   
   
sin sin 2sin .cos
2 2
sin sin 2cos .sin
2 2
cos cos 2cos .cos
2 2
cos cos 2sin sin
2 2
a b a b
a b
a b a b
a b
a b a b
a b
a b a b
a b
 
 
 
 
 
 
 
  
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
5 
§2 PHƯƠNG TRÌNH LƯỢNG GIÁC 
A. Kiến thức cơ ba ̉n 
1.Phương trình cơ bản – Phương trình bậc nhâ ́t theo mơ ̣t HSLG. 
 Tơ ̉ng qua ́t: Nếu a là mợt giá trị khơng đă ̣c biệt 
 sinx = a  
x = arcsina + k2π
x = π - arcsina + k2π



  tanx = a  x = arctana + kπ (chú y ́ k Z ) 
 cosx = a  
x = arccosa + k2π
x = -arccosa + k2π



  cotx = a  x = arccota + kπ 
Nê ́u a la ̀ mợt giá trị đă ̣c biệt: thì : 
 sinu = sinv  
u = v + k2π
u = π - v + k2π



  tanu = tanv  
u = v + kπ (chu ́ y ́ k Z ) 
 cosu = cosv  
u = v + k2π
u = -v + k2π



  cotu = cotv  u = v + kπ 
Chú y ́: 
1. Khi gặp dấu trừ ở trước thì: 
 – sinx = sin(– x) – cosx = cos( – x) 
 – tanx = tan(– x) – cotx = cot(– x) 
Khi giải phải dùng đơn vi ̣ là rad nếu đề ba ̀i khơng cho đơ ̣ (0). 
 2. Các trường hợp đặc biê ̣t: 
sinx = – 1  x = – 
2

 + k2 tanx = – 1  x = – 
4

 + k 
sinx = 0  x = k tanx = 0  x = k 
sinx = 1  x = 
2

 + k2 tanx = 1  x = 
4

 + k 
cosx = – 1  x = (2k + 1) cotx = – 1  x = – 
4

 + k 
cosx = 0  x = 
2

 + k cotx = 0  x = 
2

 + k 
cosx = 1  x = k2 cotx = 1  x = 
4

 + k 
2. Phương trình bậc hai theo mợt HSLG. 
La ̀ các phương trình ma ̀ sau khi biê ́n đơ ̉i ta được mơ ̣t trong ca ́c da ̣ng sau (a  0): 
 asin2u + bsinu + c = 0 (1)  acos2u + bcosu + c = 0 (1) 
cos sin 2 cos 2 sin
4 4
cos sin 2 cos 2 sin
4 4
x x x x
x x x x
 
 
   
   
   
   
   
   
   
   
=
=
3 sin cos 2sin 2cos
6 3
3 cos sin 2sin 2cos
3 6
x x x x
x x x x
 
 
   
       
   
   
       
   
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
6 
 đă ̣t t = sinu. điê ̀u kiê ̣n: – 1  t  1. đă ̣t t = cosu. điê ̀u kiê ̣n: – 1  t  
1. 
 (1)  at2 + bt + c = 0 (1)  at2 + bt + c = 0 
 atan2u + btanu + c = 0 (1)  acot2u + bcotu + c = 0 (1) 
 điê ̀u kiê ̣n: cosu  0. điều kiê ̣n: sinu  0. 
 đă ̣t t = tanu, (1)  at2 + bt + c = 0 đă ̣t t = cotu, (1)  at2 + bt + c = 
0 
Chu ́ y ́: Nếu phương trình co ́ chứa tanu, cotu, sin2u, cos2u, tan2u, cot2u,.. đă ̣t 
t = tanu, khi đo ́: 
1
cotu =
t
, sin2u = 
2t1
t2

, cos2u = 
2
2
t1
t1


, tan2u = 
2t1
t2

, cot2u = 
t2
t1 2
. 
3. Phương trình bậc nhâ ́t đơ ́i với sinx va ̀ cosx (Phương trình cơ ̉ điê ̉n). 
asinx + bcosx = c (1) với a, b, c  R, và a2 + b2  0 
Điều kiện để phương trình cĩ nghiệm là: a2 + b2  c2 
Chia 2 vế phương trình cho 22 ba  , ta được: 
2 2
a
a + b
sinx + 
2 2
b
a + b
cosx = 
2 2
c
a + b
Vì 
2 2
2 2 2 2
a b
+ = 1
a + b a + b
   
   
   
 nên đặt cos = 
2 2
a
a + b
, sin = 
2 2
b
a + b
Khi đo ́ ta được: sin(x + ) = 
22 ba
c

 rơ ̀i giải như phương trình cơ ba ̉n. 
Chu ́ y ́: 
Ngoa ̀i ra ta có thê ̉ du ̀ng cơng thức tính sinx, cosx theo t = 
x
tan
2
. 
Sau đây la ̀ cách gia ̉i: 
Đặt t = 
x
tan
2
. điều kiện x   + k2 
 sinu = 
2t1
t2

 va ̀ cosu = 
2
2
t1
t1


(1)  a. 
2t1
t2

 + b. 
2
2
t1
t1


 = c  (a + c)t2 – 2bt + c – 
a = 0 (2) 
Giải (2) tìm nghiệm t1, t2 nếu co ́, rơ ̀i sau đo ́ giải 
phương trình 
x
tan
2
 = t1, 
x
tan
2
 = t2 để tìm nghiệm x 
(pha ̉i tho ̉a điều kiê ̣n) 
Nê ́u a = b co ́ thê ̉ du ̀ng cơng thức sau đê ̉ gia ̉i: 
sinx  cosx = 2 sin(x  
4

) = 2 cos(x 
4

 ) 
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
7 
4. Phương trình thuần nhất bâ ̣c hai, bâ ̣c ba đới với sinx và cosx (Phương 
trình đă ̉ng câ ́p). 
 asin2x + bsinxcosx + ccos2x = 0 (1) 
 Hoặc asin2x + bsinxcosx + ccos2x = d (2) 
(2)  asin2x + bsinxcosx + ccos2x = d(sin2x + cos2x) 
  (a– d)sin2x + bsinxcosx + (c– d)cos2x = 0 (2) 
Phương trình (2) cũng là dạng (1), nên ta chỉ xe ́t dạng (1). Nếu gă ̣p da ̣ng (2) thì ta 
đưa về da ̣ng (1) như trên. 
Sau đây la ̀ cách gia ̉i da ̣ng (1): 
Nê ́u a = 0 và b, c  0 thì (1)  cosx.(bsinx + ccosx) = 0  
cosx = 0
bsinx + ccosx = 0



Nê ́u c = 0 và b, a  0 thì (1)  sinx.(asinx + bcosx) = 0  
sinx = 0
asinx + bcosx = 0



Nê ́u a, b, c  0: 
Kiểm tra xem với cosx = 0 thì (1) co ́ tho ̉a hay khơng? (cosx = 0 thì sinx =  1). 
Nếu tho ̉a thì kết luâ ̣n ră ̀ng phương trình co ́ 1 ho ̣ nghiệm là x = 
2

 + k (k  Z). 
Với cosx  0, chia 2 vê ́ của (1) cho cos2x, ta được phương trình: 
 atan2x + btanx + c = 0 (1) 
 (1) là phương trình bâ ̣c 2 theo tanx, ta đa ̃ biết ca ́ch gia ̉i (Xem phần 2). 
Nghiệm cu ̉a (1) la ̀ nghiệm cu ̉a (1) va ̀ x = 
2

 + k (nê ́u co ́). 
Chu ́ y ́: Ngoài ra ta co ́ thê ̉ dùng cơng thức ha ̣ bậc đê ̉ đưa (1) về da ̣ng phương 
trình bâ ̣c nhâ ́t theo sinx và cosx (Phâ ̀n 3). Với: 2
1- cos2x
sin x =
2
, 2
1+ cos2x
cos x =
2
, 
1
sinx.cosx = sin2x
2
Phương trình đẳng cấp bậc 3: asin3x + bsin2xcosx + c.sinxcos2x + dcos3x = 0 gia ̉i 
tương tự như đẳng cấp bậc 2. 
5. Phương trình đơ ́i xứng – Phản đơ ́i xứng. 
Dạng1: a(sinx + cosx) + bsinxcosx = c (1) 
Đặt t = sinx + cosx = 2 sin(x + 
4

) Điều kiện: – 2  t  2 
 t2 = 1 + 2sinxcosx  sinxcosx = 
2
1t2 
(1)  at + b. 
2
1t2 
 = c  bt2 + 2at – b – 2c = 0 (2) 
Giải phương trình (2), chọn nghiệm thỏa điều kiện: – 2  t  2 
Giải phương trình 2 sin(x + 
4

) = t để tìm x. 
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
8 
Dạng 2: ( pha ̉n đơ ́i xứng ) a(sinx – cosx) + bsinxcosx = c 
 (1) 
Đặt t = sinx – cosx = 2 sin(x – 
4

) Điều kiện: – 2  t  2 
 t2 = 1 – 2sinxcosx  sinxcosx = 
2
t1 2
(1)  at + b. 
2
t1 2
 = c  bt2 – 2at – b + 2c = 0 (2) 
Giải phương trình (2), chọn nghiệm thỏa điều kiện: – 2  t  2 
Giải phương trình 2 sin(x – 
4

) = t để tìm x. 
Dạng 3: a|sinx  cosx| + bsinxcosx = c (1) 
Đặt t = |sinx  cosx| = 2
π
sin(x ± )
4
 Điều kiện: 0  t  2 . Giải 
tương tự như trên. 
6. Phương trình lượng gia ́c khơng mẫu mực. 
a. Trường hợp 1: Tơ ̉ng hai sơ ́ khơng âm: 
0 0 0
0 0
A B A
A B B
    
 
   
b. Trường hợp 2: Phương pha ́p đơ ́i lập: 











MB
MA
BA
BMA
c. Trường hợp 3: Sử du ̣ng tính chất : 











NB
MA
NMBA
NBvàMA
 sinu + sinv = 2 
sinu = 1
sinv = 1

 

  sinu – sinv = 2 
sinu = 1
sinv = -1

 

 sinu + sinv = – 2 
sinu = -1
sinv = -1

 

  sinu – sinv = – 2 
sinu = -1
sinv = -1

 

 Tương tự cho ca ́c trường hợp cosu  cosv =  2 va ̀ cosu  cosv  2. 
d. Trường hợp 4: Sử du ̣ng tính chất : 

















NB
MA
NB
MA
N.MB.A
NBvàMA
 sinu.sinv = 1 
sinu = 1 sinu = -1
sinv = 1 sinv = -1
 
  
 
  sinu.sinv = 
–1 
sinu = -1 sinu = 1
sinv = 1 sinv = -1
 
  
 
 Tương tự cho ca ́c trường hợp cosu.cosv = 1, sinu.cosv = 1, cosu.sinv = 1. 
II. Ba ̀i tâ ̣p ứng du ̣ng: 
1. Phương trình cơ ban̉ – phương tri ̀nh bậc nhâ ́t mợt HSLG 
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
9 
Bài 1. Giải các phương trình sau: 
1) sinx = – 
2
3
 2) sinx = 
4
1
 3) sin(x – 600) = 
2
1
4) sin2x = – 1 5) cos(3x – 
6

) = – 
2
2
 6) cos(x – 2) = 
5
2
7) 
π 1
cos 2x + = -
3 2
 
 
 
 8) cos(2x + 500) = 
2
1
 9) tan2x = tan
7
2
10) tan(3x – 300) = – 
3
3
 11) 
π
cot 4x - = 3
6
 
 
 
 12) 
π 3
cot x + =
3 3
 
 
 
13) 
x π π
tan - = tan
2 4 8
 
 
 
 14) sin4x = 
3
2
 15) 0
x 3
cot + 20 = -
3 3
 
 
 
16) cos(3x – 450) = 
2
3
 17) sin3x = – 
2
3
 18) sin(2x – 150) = 
2
2
19) 0
x 1
sin +10 = -
2 2
 
 
 
 20) cos(x + 3) = 
3
1
 21) sin2x = 
2
3
22) cos(2x + 500) = – 
2
3
 23) 2cosx – 3 = 0 24) 3 tan3x – 3 = 0 
Bài 2. Giải các phương trình sau: 
1) cos2x . cot 




 

4
x = 0 2) 
x x
cot -1 cot +1 = 0
3 2
  
  
  
3) (cotx + 1) . sin3x = 0 4) sin2x . cotx = 0 
5) tan(x – 300)cos(2x – 1500) = 0 6) (2cos2x – 1)(2sin2x – 3 ) = 0 
8) tan(2x + 600)cos(x + 750) = 0 7) (3tanx + 3 )(2sinx – 1) = 0 
9) (2 + cosx)(3cos2x – 1) = 0 10) (sin2x – 1)(cosx + 1) = 0 
Bài 3. Giải ca ́c phương trình sau: 
1) sin(2x – 150) = 
2
2
 với – 1200 < x < 900 2) cos(2x + 10 = 
2
1
 với –  < x <  
3) sin
2
1
3
x2 




 
 với 0 < x < 2 4) tan
3
3
4
x2 




 
 với 0 < x <  
5) sinx = – 
2
1
 với –  < x < 0 6) cos(x – 2) = 
2
3
 với x  [0 ; ] 
7) tan(x – 100) = 1 với – 150 < x < 150 8) sin x
4
 
 
 
= 1 
 với x  [ ; 2] 
Bài 4. Giải các phương trình sau: 
1) cos3x – sin2x = 0 2) tanx tan2x = – 1 
3) sin3x + sin5x = 0 4) cot2x cot3x = 1 
5) sinx – cos(x + 600) = 0 6) 6) cos(x – 100) + sinx = 0 
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
10 
7) 
π π
sin x + = -sin 2x -
3 4
   
   
   
 8) 
π
cos 2x - = -cosx
4
 
 
 
9) sin3x = cos2x 10) cosx = – sin2x 
11) sin2x + cos3x = 0 12) tan(3x + 2) + cot2x = 
0 
13) tanx . tan3x = 1 14) cot2x.cot(x + 450) = 
1 
15) 
π π
cos 2x - - sin - x
4 3
   
   
   
 = 0 16) 
π π
cos 2x + + cos x -
3 6
   
   
   
 = 0 
17) tan3x + tanx = 0 18) tan3x + tan(2x – 450) 
= 0 
Bài 5. Giải các phương trình sau: 
1) sin2x = 
4
1
 2) 4cos2x – 3 = 0 3) sin23x – cos2x = 0 
2. Phương trình bâ ̣c hai – bậc ba mợt HSLG 
Bài 6. Giải các phương trình sau: 
1) 2cos2x – 2( 3 + 1)cosx + 3 + 2 = 0 2) 2cos2x + 4sinx + 1 = 0 
3) cos2x + 9cosx + 5 = 0 4) sin2x – 2cos2x + 
3
4
 = 0 
5) cos5x.cosx = cos4x.cos2x + 3cos2x + 1 6) cot4x – 4cot2x + 3 = 0 
7) cos2(x + 
3

) + 4cos( x
6

 ) = 
5
2
 8) tan2x – 
4
cosx
 + 5 = 0 
9) 
2
1
cos x
 – 1 + tanx – 3 (tanx + 1) = 0 10) cos4x – 3
2
2
1- tan x
1+ tan x
 + 2 = 0 
11) 2cos2x + 2 cosx – 2 = 0 12) 2cos2x – 3cosx + 1 = 0 
13) 6sin2x – 5sinx – 4 = 0 14) 2
x x
4cos - 2( 2 +1)cos + 2 = 0
2 2
15) 2tan 3x + (1- 3)tan3x - 3 = 0 16) 2
x x
4cot - 2( 3 -1)cot - 3 = 0
3 2
17) 23tan x - (1+ 3)tanx +1 = 0 18) cos2x + sinx + 1 = 0 
3. Phương trình bâ ̣c nhất đơí với sinx va ̀ cosx (Phương trình cơ ̉điê ̉n). 
Bài 8. Giải các phương trình sau: 
1) sinx – cosx = 
6
2
 2) 3 cosx + sinx = – 2 3) sin4x + 
3 cos4x = 3 
4) 2sinx – 9cosx = 85 5) cos(2x – 150) + sin(2x – 150) = – 1 6) cosx + 
4sinx + 1 = 0 
7) 2 sin2x + 3cos2x = 4 8) 2sinx – 2 cosx = 2 9) sin2x – 
3 cos2x = 1 
10) cosx – 3 sinx = 2 11) 3sin3x – 4cos3x = 5 12) 5cos2x 
+ 12sin2x – 13 = 0 
Nguyễn Quốc Tuấn – Bài tập tổng hợp học kì 1-tốn đại số 11 
Bạn đã tải tài liệu trên Xuctu.com. Vui lịng ủng hộ các sản phẩm của chúng tơi tại: Xuctu.com/sach/ 
11 
13) 3sinx + 3 cosx = 1 
Bài 9. Giải các phương trình sau: 
1) 2sin22x + 3 sin4x = – 3 2) cosx + 3 sinx = 2 cos x
3
 
 
 
3) 3sin3x – 3 cos9x = 1 + 4sin33x 4) 5cos(2x + 180) – 12sin(2x + 180) = –13 
5) 2cos x
6
 
 
 
 + 3cos x
3
 
 
 
= 
5 2
2
 6) sin2x + sin2x = 
1
2
7) 2sin2x + 3 sin2x = 3 8) 3cos2x – sin2x – sin2x = 0 
9) sin9x + 3 cos7x = sin7x + 3 cos9x 10) sin5x + cos5x = 2 cos13x 
11) 8sin2
x
2
 – 3sinx – 4 = 0 12) 
1+ sinx 1
=
1+ cosx 2
13) 
1- cos4x sin4x
=
2sin2x 1+ cos4x
 14) 3cosx – 4sinx + 
2
3cosx - 4sinx - 6
 = 3 
Bài 10. Tìm giá trị nho ̉ nhâ ́t, lớn nhâ ́t cu ̉a các ha ̀m sớ sau: 
1) y = 2sinx + 3 cosx + 1 2) y = 2sin2x + 4sinxcosx + 3 
3) y = sin2x + cos2x – 2 4) y = 
sinx + cosx -1
sinx - cosx + 3
4. Phương trình thuần nhất bâ ̣c hai, bâ ̣c ba đơ ́i với sinx và cosx (Phương 
trình đă ̉ng câ ́p). 
Bài 11. Giải ca ́c phương trình sau: 
1) 2sin2x + sinxcosx – 3cos2x = 0 2) 3sin2x – 4sinxcosx + 5cos2x = 2 
3) sin2x + sin2x – 2cos2x = 1
2
 4) 2cos2x + sin2x – 4sin2x = – 4 
5) sin2x – 10sinxcosx + 21cos2x = 0 6) cos2x – 3sinxcosx + 1 = 0 
7) cos2x – 3 sin2x – sin2x = 1 8) 2cos2x – 3sinxcosx + sin2x = 0 
9) 3sin2x – 2 3 sinxcosx + cos2x – 1 = 0 10) 4sin2x – 3 3 sin2x – 2cos2x = 
4 
11) 3cos2x + sinxcosx + 2sin2x = 2 12) 3cos2x + 3sinxcosx + 2sin2x = 1 
13 3 cos2x – sin2x – 3 sin2x = 1 14) 3 sin2x + 2cos2x – 1 = 0 
15) 2cos2x + 3sin2x – 8sin2x = 0 16) 3cos2x + 2sin2x – sin2x = 2 + 3 
17) sin3x + cos3x = sinx + cosx 18) sin3x + 2sin2xcosx – 3cos3x = 0 
19) sin3x – 5sin2xcosx – 3sinxcos2x + 3cos3x = 0 20) cos3x – 4cos2xsinx + 
cosxsin2x + 2sin3x = 0 
5. Phương trình đơ ́i xứng – Phản đơ ́i xứng. 
Bài 12. Giải ca ́c p