Bài tập ôn tập Chương III môn Giải tích Lớp 12 - Trường THPT Vũ Đình Liệu

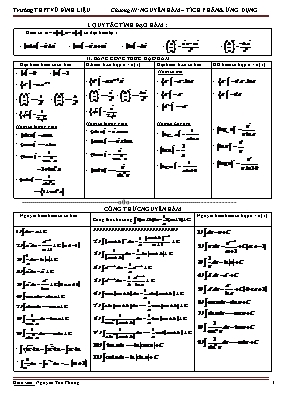
 I. QUY TẮC TÍNH ĐẠO HÀM : 
 Hàm số có đạo hàm tại x
 Ÿ Ÿ Ÿ Ÿ Ÿ
 II. BẢNG CÔNG THỨC ĐẠO HÀM
 Đạo hàm hàm số cơ bản
Đ.hàm h.số hợp u = u(x)
Đạo hàm h.số cơ bản
ĐH hàm số hợp u = u(x)
Ÿ Ÿ 
Ÿ 
Ÿ Ÿ
Ÿ
Hàm số lượng giác
Ÿ 
Ÿ 
Ÿ 
Ÿ
Ÿ
Ÿ Ÿ
Ÿ
Hàm số lượng giác
Ÿ 
Ÿ 
Ÿ 
Ÿ 
 Hàm số mũ
Ÿ 
Ÿ 
Ÿ 
Hàm số Lôgarit
Ÿ 
Ÿ
Ÿ
Ÿ 
Ÿ 
Ÿ
Ÿ
Ÿ
 ------------------------------------------------o0o-----------------------------------------------
 CÔNG THỨC NGUYÊN HÀM 
 Nguyên hàm hàm số cơ bản
Công thức bổ sung
Nguyên hàm hàm số hợp u = u(x)
*
 *
 ---------------- BÀI TẬP -----------------
Câu 1: Nguyên hàm của hàm số . 
 A. B. C. D. 
Câu 2: Nguyên hàm của hàm số . 
A. B. C. D. 
Câu 3: Nguyên hàm của hàm số l. 
A. 	 B. 	 C. 	 D. 
Câu 4: Nguyên hàm của hàm số . 
A. 	B. C. 	 D. 
Câu 5: Nguyên hàm của hàm số . 
A. 	 B. C. 	 D. 
Câu 6: Nguyên hàm của hàm số . 
A. B. 	 C. 	 D. 
Câu 7: bằng: 
A. 	 	B. C. D. 
Câu 8: bằng: 
A. 	B. 	C. 	 D. 
Câu 9: bằng: 
A. 	B. 	C. 	 D. 
Câu 10: Nguyên hàm của hàm số là: 
A. 	B. 	C. 	 D. 
Câu 11: Nguyên hàm của hàm số là: 
A. 	B. C. D. 
Câu 12: Nguyên hàm của hàm số là: 
A. 	B. 	 C. 	D. 
Câu 13: Nguyên hàm của hàm số là:
A. 	B. 	C. 	D.
Câu 14: Tínhbằng A. B. C. D. 
Câu 15: Tínhbằng A. B. C. D.
Câu 16: bằng: A. 	 B. C. D. 
Câu 17: bằng: A. B. C. D. 
Câu 18: bằng: A. B. C. D. 
Câu 19: bằng: A. 	B. C. D. 
Câu 20: là:A. 	B. 	C. 	D. 
Câu 21: A. B. C. D. 
Câu 22: A. B. C. D. 
Câu 23: Nguyên hàm của hàm số 
A. B. C. D. 
Câu 24: Nguyên hàm của hàm số 
A. B. C. D. 
Câu 25: Nguyên hàm của hàm số 
A. B. C. D. 
Câu 26: Nguyên hàm của hàm số 
A. 	B. -2 	C. 4	D. 2 
Câu 27: Tínhbằng
A. B. C. D. 
Câu 28: Tínhbằng
A. B. C. D. 
Câu 29: Tínhbằng
A. B. C. D. 
Câu 30: Nguyên hàm của là:
A. 	B. 	C. 	D. 
Câu 31: Tínhbằng
A. 	B. 	C. 	D. 
Câu 32: bằng:
A. 	B. C. 	D. 
Câu 33: Tínhbằng A. B. C. D. 
Câu 34: Tínhbằng
A. B. C. D. 
Câu 35: Tínhbằng
A. B. 	C. 	D. 
Câu 36: Tínhbằng
A. B. C. D. 
Câu 37: Tínhbằng 
A. B. C. D. 
Câu 38: Tínhbằng
A. B. C. D. 
Câu 39: Tínhbằng
 A. B. C. D. 
Câu 40: Tínhbằng A. B. C. D.
Câu 41: bằng: A. B. C. D.
Câu 42: Tínhbằng 
A. B. C. D. 
Câu 43: Tínhbằng A. B. C. D.
Câu 44: Tínhbằng 
A. B. C. D. 
Câu 45: Tínhbằng A. B. C. D. 
Câu 46: Tínhbằng A. B. C. D. 
Câu 47: Tínhbằng A. B. C. D. 
Câu 48: Tínhbằng A. B. C. D. 
Câu 49: Tínhbằng 
A. B. C. D. 
Câu 50: Tínhbằng
A. B. C. D. 
Câu 51: Tínhbằng
A. B. C. D. 
Câu 52: bằng:
A. 	B. 	C. 	D. 
Câu 53: bằng:
A. 	B. 	C. 	D. 
Câu 54: bằng:
A. 	B. 	C. 	D. 
Câu 55: bằng: A.	B. 	 C. 	D. 
Câu 56: bằng: A. 	 B. 	
 C. 	 D. 
Câu 57: Tínhbằng A. B. 
 C. D. 
Câu 58: bằng: A. B.C.	D.
Câu 59: bằng: A. 	 B. 	 C. 	 D. 
Câu 60: Tínhbằng A. 	 B. 	 C. 	 D. 
Câu 61: Tínhbằng A. 	B. 	 
 C. 	D. 
Câu 62: bằng: A. B. C. D. 
Câu 63: bằng: A. B. C. D. 
Câu 64: Tínhbằng A.	B. 	
 C. 	D. 
Câu 65: bằng: A.	 B. 	C. 	D. 
 ---------------------------------o0o—-------------------------------------
Câu 66: Tìm một nguyên hàm F(x) của hàm số , biết . 
A. B. C. D. 
Câu 67: Tìm nguyên hàm F(x) của hàm số . Biết đồ thị của hàm số F(x) đi qua điểm . 
A. B. C. D. 
Câu 68: Tìm nguyên hàm F(x) của hàm số , biết . 
A. B. C. D. 
Câu 69: Tìm nguyên hàm F(x) của hàm số . Biết đồ thị của hàm sô F(x) đi qua điểm 
A. B. C. D. 
Câu 70: Tìm hàm số biết rằng và
A. B. C. D. 
Câu 71: Tìm hàm số biết rằng và
A. B. C. D. 
Câu 72: Tìm hàm số biết rằng và
A. B. C. D. 
Câu 73: Tìm hàm số biết rằng và
A. B. C. D. 
Câu 74: Tìm hàm số biết rằng và
A. B. C. D. 
Câu 75: Tìm hàm số biết rằng ;và
A. B. C. D. 
------------------------------------Phương pháp nguyên hàm----------------------------------------------------
Câu 76: bằng: A. 	B. C. 	 D. 
Câu 77: bằng: A. 	B. 	 C. 	D. 
Câu 78: bằng: A. B. C. 	D. 
Câu 79: bằng: A. B. C. 	D. 
Câu 80: bằng: A. B. C. D. 
Câu 81: bằng: A. 	 B. C. 	D. 
Câu 82: bằng: A. 	B. 	C. 	 D. 
Câu 83: bằng: A.	B. 	 C. 	D. 
Câu 84: bằng: A. B. C. 	D. 
Câu 85: bằng: A. B. C. D.
Câu 86: bằng: A. B. C. D.
Câu 87: bằng: A. 	B.	C. 	D. 
Câu 88: bằng: A. 	 B.	C.	D.
Câu 89: bằng: A.	B.
 C.	D.
Câu 90: bằng: A. 	B. 	C.	D. 
Câu 91: bằng: A. 	B. 	C.	D. 
Câu 92: bằng: A.B.	C. D. 
Câu 93: bằng: A.B.	C. D. 
Câu 94: bằng: A.B.C. D. 
Câu 95: bằng: A.B.C. D. 
Câu 96: bằng: A. B.
 C. D. 
Câu 97: bằng:A.B.C.D.
Câu 98: bằng: A.	B.	 C.	D.
Câu 99: bằng: A.	B.	C.	 D. 
Câu 100: bằng: A.	B.	 C.	D. 
Câu 101: bằng: A.	B.	C.	D.
Câu 102: bằng: A.	B.C.	D.
Câu 103: bằng: A.B.C. D.
Câu 104: bằng: A.B. C. D.
Câu 105: bằng: A. B.
 C. D.
Câu 106: bằng: A. B. 
 C. D. 
Câu 107: bằng: A. B. C. D.
Câu 108: bằng: A.B. C. D.
Câu 109: bằng: A. B.
 C. D.
Câu 110: bằng: A. B.
 C. D.
Câu 111: bằng:A. 	B. 	 C. 	D. 
 ---------------------------------------- TÍCH PHÂN ---------------------------------------------------
Câu 112: bằng: A. 	B.	 C.	 D.
Câu 113: bằng: A. 	B. 	 C. 	D. 
Câu 114: bằng: A. 	B.	 C.	D. 
Câu 115: bằng: A. 	B. 	 C.	 D. 
Câu 116: bằng: A. 	B. 	C.	D. 
Câu 117: bằng: A. 	B. 	C. 	D. 
Câu 118: bằng: A. B. 	C.	 D.
Câu 119: bằng: A. 	B. 	C. 	D.
Câu 120: bằng: A. 	B. 	C.	D. 
Câu 121: bằng: A. 	B. 	C. 	D.
Câu 122: bằng: A. 	B. 	C. 	D. 
Câu 123: bằng: A. 	B. 	C. 	D. 
Câu 124: Cho tích phân và đặt . Khẳng định nào sau đây sai:
A.	B. 	C. 	D. 
Câu 125: Cho tích phân . Khẳng định nào sau đây sai:
A.	B. 	C. 	D.
Câu 126: Nếu đặt thì tích phân trở thành:
A).	B. 	C. 	D.
Câu 127: Nếu đặt thì tích phân trở thành:
A. 	B. 	C. 	D. 
Câu 128: Nếu đặt thì tích phân trở thành:
A. 	B. 	C. 	D. 
Câu 129: Nếu đặt thì tích phân trở thành:
A. 	B. 	C.	D. 
Câu 130: bằng: A.	B. 	C. 	D. 
Câu 131: bằng: A.	B. 	 C. 	 D. 
Câu 132: bằng: A.	B.	C. 	D. 
Câu 133: bằng: A. 	B. 	C. 	D. 
Câu 134: bằng: A.	 B. 	C.	D. 
 --------------------------Diện tích – Thể tích vật thể tròn xoay ---------------
Câu 135: Diện tích hình phẳng giới hạn bởi đồ thị hàm số ,trục hoành,và các đường thẳng .
A.	 B. 	C.	D. 
Câu 136: Diện tích hình phẳng giới hạn bởi các đường ,trục hoành,hai đường thẳng 
A.	 B. 	C.	D. 
Câu 137: Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành , trục tung, đường thẳng .
A.	 B. 	C.	D.5
Câu 138: Diện tích hình phẳng giới hạn bởi các đường . 
A.	 B. 	C.	D.
Câu 139: Diện tích hình phẳng giới hạn bởi đồ thị các h/số và .
 A.	 B. 	C.	D.
Câu 140: Diện tích hình phẳng giới hạn bởi đồ thị các h/số , và các đường thẳng 
 A.	 B. 	C.	D.
Câu 141: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục tung, truc hoành
 A.	 B. 	C.	D. 
Câu 142: Diện tích hình phẳng giới hạn bởi đồ thị hàm số ,tiệm cận ngang và các đường thẳng x = 0,x = 3.
A.	 B. 	C.	D. 
Câu 143: Tính diện tích hình phẳng giới hạn bởi các đường 
A.	 B. 	C.	D. 
Câu 144: Tính diện tích hình phẳng giới hạn bởi các đường .
A.	 B. 	C.	D. 
Câu 145: Tính diện tích hình phẳng giới hạn bởi các đường 
A.	 B. 	C.	D. 
Câu 146: Tính diện tích hình phẳng giới hạn bởi các đường 
A.	 B. 	C.	D. 
Câu 147: Tính diện tích hình phẳng giới hạn bởi các đường 
A.	 B. 	C.	D. 
Câu 148: Hình (H) giới hạn bởi các đường 
 a/ Tính diện tích hình (H). A.	 B. 	C.	 D. 
b/ Tính thể tích của vật thể tròn xoay khi (H) xoay quanh trục Ox. A.	 B. 	C.	 D. 
Câu 149: Hình (H) giới hạn bởi các đường 
 a/ Tính diện tích hình (H). A.	 B. 	C.	D. 
 b/ Tính thể tích của vật thể tròn xoay khi (H) xoay quanh trục Ox.
A.	 B. 	C.	 D. 
Câu 150: Diện tích S của hình phẳng H giới hạn bởi đồ thị hàm số, trục hoành và đường thẳng
 A.	 B. 	C.	D. 
Câu 151: Tính thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường quay quanh trục Ox. 
 A.	 B. 	C.	 D. 
Câu 152: Tính thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường quay quanh trục Ox. A.	 B. 	C.	 D. 
Câu 1: Tính thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường quay quanh trục Ox. A.	 B. 	C.	 D. 
Câu 153: Tính thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường quay quanh trục Ox. A.	 B. 	C.	 D. 
Câu 154: Hình (H) giới hạn bởi các đường và
 a/ Tính diện tích hình (H). A.	 B. 	C.	D. 
 b/ Tính thể tích của khối tròn xoay khi (H) xoay quanh trục Ox.
 A.	 B. 	 C.	 D. 
 ------------------------------------0o0-----------------------------------------------
 ŸHƯỚNG DẪN SỬ DỤNG MÁY TÍNH CASIOŸ 
 @ Chỉnh máy: Ÿ sai số cực nhỏ 9 chữ số thập phân - Bấm: Shift – mod - 9
 Ÿ Thông thường đơn vị rad - Bấm: Shift – mod - 4
cú pháp: 
1. Bài 1: Tìm nguyên hàm của hàm số : 
 Trong đó:
 Ÿ: gíá trị củatại ( A là hằng số bất kỳ thuộc tập xác định và A lấy giá trị bé 0,1; 0,2,0,31;1,1 )
 Ÿ: các kết quả nguyên hàm.
Ví dụ1: bằng A. 	B. 	 C. 	D. 
 Ÿ Bước 1: Nhập: ( RCL – A ; Shìt ) 
 Ÿ Bước 2: Gán x = A = 1 hoăc 0,1 ( bấmCALCA) cho kết quả khác 0 ta loại ngay đáp án đó Loại A
 Thay bởi đáp án B và gán A như trên ta nhận kết quả khác 0Loại B
 Thay bởi đáp án C và gán A như trên ta nhận kết quả bằng 0; chắc ăn kiểm tra thêm vài giá trị 
 của A như 0; 0,2; 0,5, 1..Chọn C. ( Không nên gán x = A giá trị quá lớn máy sẽ chữi đấy)
Ví dụ 2: bằng A. 	B. 	 C. 	D. 
 Ÿ
 Ÿ Gán A = 0,1 Cho kết quả bằng 0 - kiểm tra vài giá trị khác như 0,2; 0,3; 0,5 ta nhận kq đều bằng 0
 Chọn A. 
Ví dụ3: ()bằng A. B. 	 C. D. 
 Ÿ gán A = 0,1 nhận kết quả khác 0loai đáp án A
 Ÿ gán A = 0,1 nhận kết quả bằng 0chọn đáp án B
Cú pháp: 
 Bài 2: Tìm 1 nguyên hàm của hàm số,biết
Vi dụ 4: Tìm nguyên hàm F(x) của hàm số , biết . 
A. B. C. D.
 Ÿ gán A = 0,1; 1 đều nhận kết quả khác 0loai đáp án A
 Ÿ gán A = 0,1; 1 nhận kết quả 0, kiểm tra thêmChọn đáp án D
Vi dụ 5: Tìm1nguyên hàm F(x) của hàm số ,thỏa .
 A. B. C. D.
 Ÿ gán A = 0; 0,1 nhận kết quả khác 0loại đáp án A
 Ÿ gán A = 0; 0,1; 2 nhận kết quả 0 Chọn đáp án B
Cú pháp: 
 Bài toán 3: Tính tích phân: 
 ( Trong các đáp án đều là số vô tỷ: dạng căn, số e, sốcác em nên bấm máy ghi nhận lại các các kết quả trên )
Ví dụ 6: bằng: A. 	B.	 C.	D. 
Ví dụ 7: bằng: A.	 B. 	C.	D. 
 Ÿ Ÿ Ÿ Ÿ
Ví dụ 8: bằng: A.	 B. 	 C.	D. 
Ví dụ 9: A. B. C. D. 
Ví dụ 10: A. B. C. D. 
Bài toán 4: Diện tích hình phẳng – Thể tích khối tròn xoay:
Cú pháp: 
Ví dụ 10: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số , là
A. B. 	C. 	D. 
 Ÿ Phương trình HĐGĐ
 Ÿ
Ví dụ 11: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số , là
A. 	B. 	C. 	D. 
 Ÿ Phương trình HĐGĐ
 Ÿ 
Ví dụ 12: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số , là
A. 	B. 	C. 	D. 
 Ÿ Phương trình HĐGĐ
 Ÿ
Ví dụ 13: Tính diện tích hình phẳng giới hạn bởi các đường: và 
 A. 	B. 	C. 	D. 
 Ÿ Phương trình HĐGĐ
 Ÿ
Ví dụ 14. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số , là
A. 	B. 	C. 	D. 
 Ÿ Phương trình HĐGĐ:
 Ÿ chọn C 
Ví dụ 15. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số , là
A. 	B. 	C. 	D. 
 Ÿ 
 Ÿ Phương trình TĐGĐ:
 Ÿ chọn A 
Ví dụ 16: Hình (H) giới hạn bởi các đường Tính thể tích của vật thể tròn xoay khi (H) xoay quanh trục Ox. A.	 B. 	 C.	 D. 
 Ÿ chọn A
Ví dụ 17: Tính thể tích của khối tròn xoay khi (H) giới hạn bởi các đường vàxoay quanh trục Ox. A.	 B. 	 C.	 D. 
 Ÿ Phương trình HĐGĐ:
 Ÿ chọn A
Các em thực hành tiếp
Ví dụ 18: Tính thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường quay quanh trục Ox. A.	 B. 	C.	 D. 
Ví dụ 19: Tính thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường quay quanh trục Ox. A.	 B. 	C.	 D. 
Ví dụ 20: Tính thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường quay quanh trục Ox. A.	 B. 	C.	 D. 
Ví dụ 20: Tính thể tích của vật thể tròn xoay giới hạn bởi các đường xoay quanh trục Ox
 A.	 B. 	C.	 D. 
 -------------------------------------0O0----------------------------------------------
 ĐỀ KIỂM TRA 1 TIẾT – Tham khảo ( THPT chuyên LÊ HỒNG PHONG )
Câu 1. Cho hàm số . Hàm số nào sau đây không phải là nguyên hàm của :
	A. 	B. 	
	C. 	D. 
Câu 2. Cho hàm số . Một nguyên hàm của là:
	A. 	B. 	C.	D.
Câu 3. Cho hàm số . Một nguyên hàm của là:
	A. 	B. 	C.	D.
Câu 4. . Cho hàm số . Hàm số nào sau đây không phải là nguyên hàm của :
	A. 	B.	C. 	D. 
Câu 5. Cho hàm số . Một nguyên hàm của là:
	A. 	B. 	C.	D.
Câu 6. Cho hàm số . Một nguyên hàm của là: A. 	 B.	 C.	 D.
Câu 7. H.slà ng.hàm của hàm nào trong các hàm sau:A. 	 B.
 	C. D.
Câu 8. Cho với là phân số tối giản. Khi đó A.39 B. 31 C. 9 D. 140
Câu 9. Cho . Khi đó A. 17 B. 70 C. -3	 D. 7
Câu 10. Cho . Khi đó A. B. 	C. D.
Câu 11. Cho . Đặt , ta có :	
A. B. C. D. 
Câu 12. Chọn phát biểu sai: A. B. 
 C. 	D. 
Câu 13. Cho . Khi đó A. 	B. 	 C. 	D. 
Câu 14. Cho hàm số liên tục trên . Chọn khẳng định sai: A. B. 	 C. D. 
Câu 15. Cho hàm số liên tục trên .Chọn phát biểu sai:
	A. nếu là hàm số lẻ.	B. nếu là hàm số chẵn.	
 C. 	D. 
Câu 16. Diện tích hình phẳng giới hạn bởi đồ thị hàm số liên tục trên , trục Ox, , được xác định bởi công thức: A. B. C. 	 D. 
Câu 17. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số , là A. B. C. 	D. 
Câu 18. Thể tích khối tròn xoay do hình phẳng (H) giới hạn bởi đồ thị hàm số , trục Ox, ,khi quay quanh trục Ox là A. B. 3 	C. 	D. 
Câu 19. Thể tích vật thể có đáy là đường tròn xác định bởi , mỗi thiết diện vuông góc với trục Ox là một hình vuông là: A. 5 B. 4	 C. D. 
Câu 20. Tìm phát biểu đúng trong các phát biểu sau: A. B. 	
	 C. 	D. 
Câu 21. Tìm phát biểu sai trong các phát biểu sau: A. 	 B. 	
	 C. 	D. 
Câu 22. Cho . Đặt , ta có  A. 	B. 	
 C. 	D. 
Câu 23 Thể tích khối tròn xoay do hình phẳng (H) giới hạn bởi đồ thị hàm số , ,và tiếp tuyến của (C) tại điểm có hoành độ bằng 1 khi quay quanh trục Oy là: A. B. C. 	D. 
Câu 24. Diện tích hình phẳng giới hạn bởi đồ thị các hs , là A. B. C. D. 
Câu 25. Cho . Tìm phát biểu sai: A. B. C. D. 
 --------------------------------0o0---------------------------------------------