Bài tập Giải tích 12 - Khảo sát hàm số

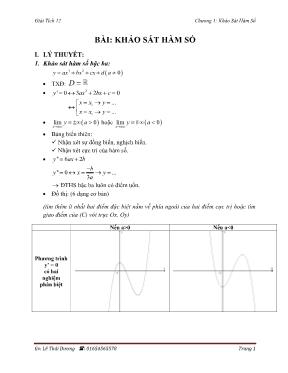
Giải Tích 12 Chương 1: Khảo Sát Hàm Số 
Gv: Lê Thái Dương : 01654565578 Trang 1 
BÀI: KHẢO SÁT HÀM SỐ 
I. LÝ THUYẾT: 
1. Khảo sát hàm số bậc ba: 
 3 2 0y ax bx cx d a     
 TXĐ: D  
 2' 0 3 2 0y ax bx c     
1
1
...
...
x x y
x x y
  
 
  
  lim 0
x
y a

   hoặc  lim 0
x
y a

   
 Bảng biến thiên: 
 Nhận xét sự đồng biến, nghịch biến. 
 Nhận xét cực trị của hàm số. 
 '' 6 2y ax b  
'' 0 ...
3
b
y x y
a

     
 ĐTHS bậc ba luôn có điểm uốn. 
 Đồ thị: (6 dạng cơ bản) 
(tìm thêm ít nhất hai điểm đặc biệt nằm về phía ngoài của hai điểm cực trị hoặc tìm 
giao điểm của (C) với trục Ox, Oy) 
 Nếu a>0 Nếu a<0 
Phương trình 
y’ = 0 
có hai 
nghiệm 
phân biệt 
Giải Tích 12 Chương 1: Khảo Sát Hàm Số 
Gv: Lê Thái Dương : 01654565578 Trang 2 
Phương trình 
y’ = 0 
có nghiệm 
kép 
Phương trình 
y’ = 0 
vô nghiệm 
 Chú ý: Đồ thì hàm số bậc ba luôn nhận điểm uốn làm tâm đồi xứng. 
2. Khảo sát hàm số trùng phương: 
 4 2 0y ax bx c a    
 TXĐ: D  
  3 2' 4 2 2 2y ax bx x ax b    
2
0
' 0
2 0
x
y
ax b

  
 
  lim 0
x
y a

   hoặc  lim 0
x
y a

   
 Bảng biến thiên: 
 Nhận xét sự đồng biến, nghịch biến. 
 Nhận xét cực trị của hàm số. 
 2'' 12 2y ax b  
Giải Tích 12 Chương 1: Khảo Sát Hàm Số 
Gv: Lê Thái Dương : 01654565578 Trang 3 
2'' 0
6
b
y x
a

   
 ĐTHS trùng phương hoặc có 2 điểm uốn hoặc không có điểm uốn nào. 
 Đồ thị: (4 dạng cơ bản) 
(tìm thêm ít nhất hai điểm đặc biệt nằm về hai phía của trục Oy hoặc tìm giao 
điểm của (C) với trục Ox, Oy) 
 a>0 a<0 
Phương trình 
y’ = 0 
có ba nghiệm 
phân biệt 
Phương trình 
y’ = 0 
có một nghiệm 
 Chú ý: Đồ thì hàm sốtrùng phương luôn nhận trục tung làm trục đối xứng. 
3. Khảo sát hàm số nhất biến: 
 0, 0
ax b
y c D ad bc
cx d

    

 TXĐ: \
d
D
c
 
  
 
Giải Tích 12 Chương 1: Khảo Sát Hàm Số 
Gv: Lê Thái Dương : 01654565578 Trang 4 
 
   
2 2
'
a b
c d ad bc
y
cx d cx d

 
 
 0 ' 0,ad bc y x D      
 0 ' 0,ad bc y x D      
 Tiệm cận: (phải tìm giới hạn) 
 TCĐ: 
d
x
c
   TCN: 
a
y
c
 
 Bảng biến thiên: (2 dạng) 
 0ad bc  : 
x - 
c
d
 + 
y’ + + 
y 
c
a
+ 
- 
c
a
 HS đồng biến trên ;
d
c
 
 
 
 và ;
d
c
 
 
 
 0ad bc  : 
x - 
c
d
 + 
y’ - - 
y c
a
- 
+ 
c
a
 HS nghịch biến trên ;
d
c
 
 
 
 và ;
d
c
 
 
 
 Đồ thị: (2 dạng cơ bản) 
Giải Tích 12 Chương 1: Khảo Sát Hàm Số 
Gv: Lê Thái Dương : 01654565578 Trang 5 
0D ad bc   0D ad bc   
 Chú ý: Đồ thị hàm số nhất biến luôn nhận giao điểm hai đường tiệm cận làm tâm đối 
xứng. 
II. BÀI TẬP: 
Bài 1. Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba 
a) 132 23  xxy 
b) 533 23  xxxy 
c) 863 23  xxxy 
d) 
3
1
3
2 23  xxy 
e) xxy 4
3
1 3  
f) 133 23  xxxy 
g) 393 23  xxxy 
h) xxy 33  
i) xxy 33  
j) 43
3
1 23 

 xxxy 
Bài 2. Khảo sát sự biến thiên và vẽ đồ thị hàm số trùng phương 
a) 
2
5
3
2
2
4
 x
x
y 
b) 22 )1()1(  xxy 
c) 45 24  xxy 
d) 32 24  xxy 
e) 4xy  
f) 56 24  xxy 
g) 
4
9
2
4
1 24  xxy 
h) 4223 xxy  
i) 12 24  xxy 
j) 34 24  xxy 
Bài 3. Khảo sát sự biến thiên và vẽ đồ thị hàm nhất biến 
Giải Tích 12 Chương 1: Khảo Sát Hàm Số 
Gv: Lê Thái Dương : 01654565578 Trang 6 
a) 
2
12



x
x
y 
b) 
1
2



x
x
y 
c) 
3
2



x
x
y 
d) 
2
12



x
x
y 
e) 
x
y
1
 
f) 
1
12



x
x
y 
g) 
3
13



x
x
y 
h) 
2
2



x
x
y 
i) 
2
23



x
x
y 
j) 
22
1



x
y 
Bài 4. Khảo sát và vẽ đồ thị hàm số hữu tỉ 
a) 
2 1
1
x x
y
x
 


b) 
2 2 3
2
x x
y
x
 


c) 
2 2
1
x x
y
x
 


d) 
2 2 2
1
x x
y
x
 

