Bài tập chương II - Hình học 10

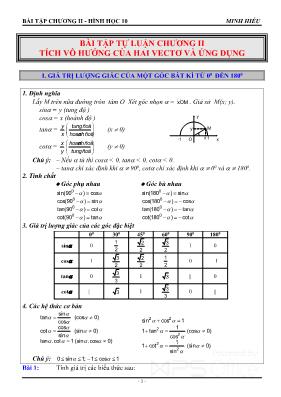
BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 1 -
O x
y
M
x
y

1-1
BÀI TẬP TỰ LUẬN CHƯƠNG II
TÍCH VƠ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GĨC BẤT KÌ TỪ 00 ĐẾN 1800
1. Định nghĩa
Lấy M trên nữa đường trịn tâm O Xét gĩc nhọn  = xOM . Giả sử M(x; y).
sin = y (tung độ )
cos = x (hồnh độ )
tan =
y tungđộ
x hoànhđộ
 
 
 
(x  0)
cot =
x hoànhđộ
y tungđộ
 
 
 
(y  0)
Chú ý: – Nếu  tù thì cos < 0, tan < 0, cot < 0.
– tan chỉ xác định khi   900, cot chỉ xác định khi   00 và   1800.
2. Tính chất
 Gĩc phụ nhau  Gĩc bù nhau
0
0
0
0
sin(90 ) cos
cos(90 ) sin
tan(90 ) cot
cot(90 ) tan
 
 
 
 
 
 
 
 
0
0
0
0
sin(180 ) sin
cos(180 ) cos
tan(180 ) tan
cot(180 ) cot
 
 
 
 
 
  
  
  
3. Giá trị lượng giác của các gĩc đặc biệt
00 300 450 600 900 1800
sin 0
1
2
2
2
3
2
1 0
cos 1
3
2
2
2
1
2
0 –1
tan 0
3
3
1 3  0
cot  3 1
3
3
0 
4. Các hệ thức cơ bản
sin
tan (cos 0)
cos
cos
cot (sin 0)
sin
tan .cot 1 (sin .cos 0)

 


 

   
 
 
 
2 2
2
2
2
2
sin cos 1
1
1 tan (cos 0)
cos
1
1 cot (sin 0)
sin
 
 

 

 
  
  
Chú ý: 0 sin 1; 1 cos 1     
Bài 1: Tính giá trị các biểu thức sau:
BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 2 -
O
A
B
a

b

a

b

a) a b c0 0 0sin0 cos0 sin90  b) a b c0 0 0cos90 sin90 sin180 
c) a b c2 0 2 0 2 0sin90 cos90 cos180  d) 2 0 2 0 2 03 sin 90 2cos 60 3tan 45  
e) a a a2 2 0 0 2 0 24 sin 45 3( tan45 ) (2 cos45 ) 
Bài 2: Tính giá trị của các biểu thức sau:
a) x xsin cos khi x bằng 00; 450; 600. b) x x2sin cos2 khi x bằng 450; 300.
Bài 3: Cho biết một giá trị lượng giác của một gĩc, tính các giá trị lượng giác cịn
lại:
a)
1
sin
4
  ,  nhọn. b)
1
cos
3
   c) xtan 2 2
Bài 4: Biết 0
6 2
sin15
4

 . Tinh 0 0 0cos15 , tan15 , cot15 .
Bài 5: Cho biết một giá trị lượng giác của một gĩc, tính giá trị của một biểu thức:
a) x x0 0
1
sin , 90 180
3
   . Tính
x x
A
x x
tan 3cot 1
tan cot
 


.
b) tan 2  . Tính B
3 3
sin cos
sin 3cos 2sin
 
  


 
Bài 6: Chứng minh các đẳng thức sau:
a) x x x x2(sin cos ) 1 2sin .cos   b) x x x x4 4 2 2sin cos 1 2sin .cos  
c) x x x x2 2 2 2tan sin tan .sin  d) x x x x6 6 2 2sin cos 1 3sin .cos  
e) x x x x x xsin .cos (1 tan )(1 cot ) 1 2sin .cos   
f)
Bài 7: Rút gọn các biểu thức sau:
a) y y ycos sin .tan b) b b1 cos . 1 cos  c) a a2sin 1 tan
d)
x
x x
x
2
2
1 cos
tan .cot
1 sin



e)
x x
x x
2 2
2
1 4sin .cos
(sin cos )


f) x x x x x0 0 2 2 2sin(90 ) cos(180 ) sin (1 tan ) tan     
g) cos10 + cos20 + ............+ cos170 + cos180
Bài 8: Tính giá trị các biểu thức sau:
a) 2 0 2 0 2 0 2 0cos 12 cos 78 cos 1 cos 89   b) 2 0 2 0 2 0 2 0sin 3 sin 15 sin 75 sin 87  
II. TÍCH VƠ HƯỚNG CỦA HAI VECTƠ
1. Gĩc giữa hai vectơ
Cho a b, 0
 
. Từ một điểm O bất kì vẽ OA a OB b, 
  
.
Khi đĩ   a b AOB, 

với 00  AOB  1800.
Chú ý:
+  a b,

= 900  a b

BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 3 -
+  a b,

= 00  a b,

cùng hướng
+  a b,

= 1800  a b,

ngược hướng
+    a b b a, ,
  
2. Tích vơ hướng của hai vectơ
 Định nghĩa:  a b a b a b. . .cos ,
    
.
Đặc biệt: a a a a
22.  
   
.
 Tính chất: Với a b c, ,
 
bất kì và kR, ta cĩ:
+ . .a b b a
  
;   . .a b c a b a c  
     
;
     . . .ka b k a b a kb 
    
; 2 20; 0 0a a a   
  
.
+  
2 2 22 .a b a a b b   
    
;  
2 2 22 .a b a a b b   
    
;   2 2a b a b a b   
    
.
+ .a b

> 0  ,a b

nhọn
.a b

= 0  ,a b

vuơng
.a b

< 0  ,a b

tù
3. Biểu thức toạ độ của tích vơ hướng
 Cho a = (a1, a2), b

= (b1, b2). Khi đĩ: a b a b a b1 1 2 2.  

.
 a a a2 21 2 

;
a b a b
a b
a a b b
1 1 2 2
2 2 2 2
1 2 1 2
cos( , )
.


 

; a b a b a b1 1 2 2 0   

 Cho A A B BA x y B x y( ; ), ( ; ) . Khi đĩ: B A B AAB x x y y
2 2( ) ( )    .
Bài 1: Cho tam giác ABC vuơng tại A, AB = a, BC = 2a. Tính các tích vơ hướng:
a) AB AC.
 
b) ACCB.
 
c) ABBC.
 
Bài 2: Cho tam giác ABC đều cạnh bằng a. Tính các tích vơ hướng:
a) AB AC.
 
b) ACCB.
 
c) ABBC.
 
Bài 3: Cho bốn điểm A, B, C, D bất kì.
a) Chứng minh:DABC DBCA DC AB. . . 0  
     
.
b) Từ đĩ suy ra một cách chứng minh định lí: "Ba đường cao trong tam giác đồng qui".
Bài 4: Cho tam giác ABC với ba trung tuyến AD, BE, CF. Chứng minh:
BC AD CABE ABCF. . . 0  
     
.
Bài 5: Cho hai điểm M, N nắm trên đường trịn đường kính AB = 2R. Gọi I là giao
điểm của hai đường thẳng AM và BN.
a) Chứng minh: AM AI AB AI BN BI BABI. . , . . 
       
.
b) Tính AM AI BN BI. .
   
theo R.
Bài 6: Cho tam giác ABC cĩ AB = 5, BC = 7, AC = 8.
a) Tính AB AC.
 
, rồi suy ra giá trị của gĩc A.
b) Tính CACB.
 
.
c) Gọi D là điểm trên CA sao cho CD = 3. Tính CDCB.
 
.
Bài 7: Cho hình vuơng ABCD cạnh a. Tính giá trị các biểu thức sau:
BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 4 -
a) AB AC.
 
b) AB AD BD BC( )( ) 
   
c) AC AB AD AB( )(2 ) 
   
d) ABBD.
 
e) AB AC AD DA DB DC( )( )   
     
HD: a) a2 b) a2 c) a22 d) a2 e) 0
Bài 8: Cho tam giác ABC cĩ AB = 2, BC = 4, CA = 3.
a) Tính AB AC.
 
, rồi suy ra cosA.
b) Gọi G là trọng tâm của ABC. Tính AGBC.
 
.
c) Tính giá trị biểu thức S = GAGB GBGC GCGA. . . 
     
.
d) Gọi AD là phân giác trong của gĩc BAC (D  BC). Tính AD

theo AB AC,
 
, suy ra
AD.
HD: a) AB AC
3
.
2
 
 
, A
1
cos
4
  b) AGBC
5
.
3

 
c) S
29
6
 
d) Sử dụng tính chất đường phân giác
AB
DB DC
AC
.
 
 AD AB AC
3 2
5 5
 
  
, AD
54
5

Bài 9: Cho tam giác ABC cĩ AB = 2, AC = 3, A = 600. M là trung điểm của BC.
a) Tính BC, AM.
b) Tính IJ, trong đĩ I, J được xác định bởi: IA IB JB JC2 0, 2  
   
.
HD: a) BC = 19 , AM =
7
2
b) IJ =
2
133
3
Bài 10: Cho tứ giác ABCD.
a) Chứng minh AB BC CD DA AC DB2 2 2 2 2 .   
 
.
b) Suy ra điều kiện cần và đủ để tứ giác cĩ hai đường chéo vuơng gĩc là:
AB CD BC DA2 2 2 2   .
Bài 11: Cho tam giác ABC cĩ trực tâm H, M là trung điểm của BC. Chứng minh:
MH MA BC2
1
.
4

 
.
Bài 12: Cho hình chữ nhật ABCD, M là một điểm bất kì. Chứng minh:
a) MA MC MB MD2 2 2 2   b) MAMC MBMD. .
   
c) MA MBMD MAMO2 . 2 . 
   
(O là tâm của hình chữ nhật).
Bài 13: Cho tam giác ABC cĩ A(1; –1), B(5; –3), C(2; 0).
a) Tính chu vi và nhận dạng tam giác ABC.
b) Tìm toạ độ điểm M biết CM AB AC2 3 
  
.
c) Tìm tâm và bán kính đường trịn ngoại tiếp tam giác ABC.
Bài 14: Cho tam giác ABC cĩ A(1; 2), B(–2; 6), C(9; 8).
a) Tính AB AC.
 
. Chứng minh tam giác ABC vuơng tại A.
b) Tìm tâm và bán kính đường trịn ngoại tiếp tam giác ABC.
c) Tìm toạ độ trực tâm H và trọng tâm G của tam giác ABC.
d) Tính chu vi, diện tích tam giác ABC.
e) Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng.
f) Tìm toạ độ điểm N trên Ox để tam giác ANC cân tại N.
g) Tìm toạ độ điểm D để ABDC là hình chữ nhật.
h) Tìm toạ độ điểm K trên Ox để AOKB là hình thang đáy AO.
i) Tìm toạ độ điểm T thoả TA TB TC2 3 0  
   
BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 5 -
k) Tìm toạ độ điểm E đối xứng với A qua B.
l) Tìm toạ độ điểm I chân đường phân giác trong tại đỉnh C của ABC.
Bài 15: Cho tam giác ABC. tìm tập hợp những điểm M sao cho:
a) MA MAMB2 2 .
 
b) MA MB MB MC( )(2 ) 0  
   
c) MA MB MB MC( )( ) 0  
   
d) MA MAMB MAMC22 . . 
   
Bài 16: Cho hình vuơng ABCD cạnh a, tâm O. Tìm tập hợp những điểm M sao cho:
a) MAMC MBMD a2. . 
   
b) MAMB MC MD a2. . 5 
   
c) MA MB MC MD2 2 2 23   d) MA MB MC MC MB a2( )( ) 3   
    
Bài 17: Cho tứ giác ABCD, I, J lần lượt là trung điểm của AB và CD. Tìm tập hợp
điểm M sao cho: MAMB MC MD IJ2
1
. .
2
 
   
.
Bài 18: Cho hình thang vuơng ABCD, đường cao AB=2a, đáy lớn BC=3a, đáy nhỏ
AD=2a.
III. HỆ THỨC LƯỢNG TRONG TAM GIÁC
Cho ABC cĩ: – độ dài các cạnh: BC = a, CA = b, AB = c
– độ dài các đường trung tuyến vẽ từ các đỉnh A, B, C: ma, mb, mc
– độ dài các đường cao vẽ từ các đỉnh A, B, C: ha, hb, hc
– bán kính đường trịn ngoại tiếp, nội tiếp tam giác: R, r
– nửa chu vi tam giác: p
– diện tích tam giác: S
1. Định lí cơsin
a b c bc A2 2 2 2 .cos   ; b c a ca B2 2 2 2 .cos   ; c a b ab C2 2 2 2 .cos  
2. Định lí sin
a b c
R
A B C
2
sin sin sin
  
3. Độ dài trung tuyến
a
b c a
m
2 2 2
2 2( )
4
 
 ; b
a c b
m
2 2 2
2 2( )
4
 
 ; c
a b c
m
2 2 2
2 2( )
4
 

4. Diện tích tam giác
S = a b cah bh ch
1 1 1
2 2 2
 
= bc A ca B ab C
1 1 1
sin sin sin
2 2 2
 
=
abc
R4
= pr
BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 6 -
A
B CH
OM
A
B
C
D
T
R
= p p a p b p c( )( )( )   (cơng thức Hê–rơng)
Giải tam giác là tính các cạnh và các gĩc của tam giác khi biết một số yếu tố cho trước.
5. Hệ thức lượng trong tam giác vuơng (nhắc lại)
Cho ABC vuơng tại A, AH là đường cao.
 BC AB AC2 2 2  (định lí Pi–ta–go)
 AB BC BH2 . , AC BCCH2 .
 AH BH CH2 . ,
AH AB AC2 2 2
1 1 1
 
 AH BC AB AC. .
 b a B a C c B c C.sin .cos tan cot    ; c a C a B b C b C.sin .cos tan cot   
6. Hệ thức lượng trong đường trịn (bổ sung)
Cho đường trịn (O; R) và điểm M cố định.
 Từ M vẽ hai cát tuyến MAB, MCD.
PM/(O) = MAMB MC MD MO R2 2. .  
   
 Nếu M ở ngồi đường trịn, vẽ tiếp tuyến MT.
PM/(O) = MT MO R2 2 2 
Bài 1: Chứng minh rằng trong mọi tam giác ABC ta cĩ;
a) a b C c B.cos .cos  b) A B C C Bsin sin cos sin cos 
c) ah R B C2 sin sin d) a b cm m m a b c
2 2 2 2 2 23 ( )
4
    
e)  ABCS AB AC AB AC
2
2 21 . .
2
 
 
Bài 2: Cho tam giác ABC. Chứng minh rằng:
a) Nếu b + c = 2a thì
a b ch h h
2 1 1
  b) Nếu bc = a2 thì b c aB C A h h h
2 2sin sin sin , 
c) A vuơng b c am m m
2 2 25 
Bài 3: Cho tứ giác lồi ABCD, gọi  là gĩc hợp bởi hai đường chép AC và BD.
a) Chứng minh diện tích S của tứ giác cho bởi cơng thức: S AC BD
1
. .sin
2
 .
b) Nêu kết quả trong trường hợp tứ giác cĩ hai đường chéo vuơng gĩc.
Bài 4: Cho ABC vuơng ở A, BC = a, đường cao AH.
a) Chứng minh AH a B B BH a B CH a B2 2.sin .cos , .cos , .sin   .
b) Từ đĩ suy ra AB BC BH AH BH HC2 2. , .  .
Bài 5: Cho AOB cân đỉnh O, OH và OK là các đường cao. Đặt OA = a, AOH  .
a) Tính các cạnh của OAK theo a và .
b) Tính các cạnh của các tam giác OHA và AKB theo a và .
c) Từ đĩ tính sin2 , cos2 , tan2   theo sin , cos , tan   .
Bài 6: Giải tam giác ABC, biết:
a)  c A B0 014; 60 ; 40   b)  b A C0 04,5; 30 ; 75  
c)  c A C0 035; 40 ; 120   d)  a B C0 0137,5; 83 ; 57  
BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 7 -
Bài 7: Giải tam giác ABC, biết:
a) a b C 06,3; 6,3; 54   b) b c A 032; 45; 87  
c) a b C 07; 23; 130   d) b c A 014; 10; 145  
Bài 8: Giải tam giác ABC, biết:
a) a b c14; 18; 20   b) a b c6; 7,3; 4,8  
c) a b c4; 5; 7   d) a b c2 3; 2 2; 6 2   
$ BÀI TẬP ƠN CHƯƠNG II $
Bài 1: Chứng minh các đẳng thức sau:
a)
x x
x x x
sin 1 cos 2
1 cos sin sin

 

b)
x x
x x
x x
3 3sin cos
1 sin .cos
sin cos

 

c)
x
x x x
2
2
2 2
tan 1 1
1
2tan 4sin .cos
 
   
 
d)
x x
x
x x x
2 2
2
4 4 2
cos sin
1 tan
sin cos sin

 
 
e)
x x
x x
x x x x
2 2sin cos
sin cos
cos (1 tan ) sin (1 cot )
  
 
f)
x x
x x
x x x x
cos sin 1
tan . cot
1 sin 1 cos sin .cos
   
     
    
g) x x x x x2 2 2 2 2cos (cos 2sin sin tan ) 1  
Bài 2: Biết 0
5 1
sin18
4

 . Tính cos180, sin720, sin1620, cos1620, sin1080, cos1080,
tan720.
Bài 3: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:
a) A = x x x4 2 2cos cos sin  b) B = x x x4 2 2sin sin cos 
Bài 4: Cho các vectơ a b,

.
a) Tính gĩc  a b,

, biết a b, 0
 
và hai vectơ u a b v a b2 , 5 4   
    
vuơng gĩc.
b) Tính a b

, biết a b a b11, 23, 30   
  
.
c) Tính gĩc  a b,

, biết a b a b a b a b( 3 ) (7 5 ), ( 4 ) (7 2 )     
      
.
d) Tính a b a b, 2 3 
  
, biết a b a b 03, 2, ( , ) 120  
  
.
e) Tính a b,

, biết a b a b a b a b2, 4, (2 ) ( 3 )      
      
.
Bài 5: Cho tam giác ABC cĩ AB = 3, AC = 4, BC = 6.
a) Tính AB AC.
 
và cosA.
b) M, N là hai điểm được xác định bởi AM AB AN AC
2 3
,
3 4
 
   
. Tính MN.
Bài 6: Cho hình bình hành ABCD cĩ AB = 3 , AD = 1, BAD 060 .
a) Tính AB AD BABC. , .
   
.
b) Tính độ dài hai đường chéo AC và BD. Tính  AC BDcos ,
 
.
Bài 7: Cho tam giác ABC cĩ gĩc A nhọn. Về phía ngồi tam giác vẽ các tam giác
vuơng cân đỉnh A là ABD và ACE. Gọi I là trung điểm của BC. Chứng minh AI  DE.
Bài 8: Cho tứ giác ABCD cĩ hai đường chéo cắt nhau tại O. Gọi H, K lần lượt là
trực tâm của các tam giác ABO và CDO. Gọi I, J lần lượt là trung điểm của AD và BC.
BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 8 -
Chứng minh HK  IJ.
Bài 9: Cho hình vuơng ABCD cĩ cạnh bằng 1, M là trung điểm cạnh AB. Trên
đường chéo AC lấy điểm N sao cho AN AC
3
4

 
.
a) Chứng minh DN vuơng gĩc với MN.
b) Tính tổng DN NC MNCB. .
   
.
Bài 10: Cho tam giác ABC. Tìm tập hợp các điểm M sao cho:
a) AB AM AC AM. . 0 
   
b) AB AM AC AM. . 0 
   
c) MA MB MA MC( )( ) 0  
   
d) MA MB MC MA MB MC( 2 )( 2 ) 0    
     
Bài 11: Chứng minh rằng trong mọi tam giác ABC ta cĩ:
a) b c a b C c B2 2 ( .cos .cos )   b) b c A a c C b B2 2( )cos ( .cos .cos )  
b) A B C C B B Csin sin .cos sin .cos sin( )   
Bài 12: Cho ABC. Chứng minh rằng:
a) Nếu a b c b c a bc( )( ) 3     thì A 060 .
b) Nếu
b c a
a
b c a
3 3 3
2  
 
thì A 060 .
c) Nếu A C Bcos( ) 3cos 1   thì B 060 .
d) Nếu b b a c a c2 2 2 2( ) ( )   thì A 060 .
Bài 13: Cho ABC. Chứng minh rằng:
a) Nếu
b a
b A a B
c
2 2
cos cos
2

  thì ABC cân đỉnh C.
b) Nếu
B
A
C
sin
2cos
sin
 thì ABC cân đỉnh B.
c) Nếu a b C2 .cos thì ABC cân đỉnh A.
d) Nếu
b c a
B C B Ccos cos sin .sin
  thì ABC vuơng tại A.
e) Nếu S R B C22 sin .sin thì ABC vuơng tại A.
Bài 14: Cho ABC. Chứng minh điều kiện cần và đủ để hai trung tuyến BM và CN
vuơng gĩc với nhau là: b c a2 2 25  .
Bài 15: Cho ABC.
a) Cĩ a = 5, b = 6, c = 3. Trên các đoạn AB, BC lần lượt lấy các điểm M, K sao cho
BM = 2, BK = 2. Tính MK.
b) Cĩ A
5
cos
9
 , điểm D thuộc cạnh BC sao cho  ABC DAC , DA = 6, BD
16
3
 . Tính
chu vi tam giác ABC.
HD: a) MK =
8 30
15
b) AC = 5, BC =
25
3
, AB = 10
Bài 16: Cho một tam giác cĩ độ dài các cạnh là: x x x x2 21; 2 1; 1    .
a) Tìm x để tồn tại một tam giác như trên.
b) Khi đĩ chứng minh tam giác ấy cĩ một gĩc bằng 0120 .
Bài 17: Cho ABC cĩ B 090 , AQ và CP là các đường cao, ABC BPQS S9  .
BÀI TẬP CHƯƠNG II - HÌNH HỌC 10 MINH HIẾU
- 9 -
a) Tính cosB.
b) Cho PQ = 2 2 . Tính bán kính R của đường trịn ngoại tiếp ABC.
HD: a) B
1
cos
3
 b) R
9
2

Bài 18: Cho ABC.
a) Cĩ B 060 , R = 2, I là tâm đường trịn nội tiếp. Tính bán kính của đường trịn ngoại
tiếp ACI.
b) Cĩ A 090 , AB = 3, AC = 4, M là trung điểm của AC. Tính bán kính đường trịn
ngoại tiếp BCM.
c) Cĩ a = 4, b = 3, c = 2, M là trung điểm của AB. Tính bán kính của đường trịn ngoại
tiếp BCM.
HD: a) R = 2 b) R
5 13
6
 c) R
8 23
3 30

Bài 19: Cho hai đường trịn (O1, R) và (O2, r) cắt nhau tại hai điểm A và B. Một
đường thẳng tiếp xúc với hai đường trịn tại C và D. Gọi N là giao điểm của AB và CD (B
nằm giữa A và N). Đặt  AOC AO D1 2,   .
a) Tính AC theo R và ; AD theo r và .
b) Tính bán kính của đường trịn ngoại tiếp ACD.
HD: a) AC = R2 sin
2

, AD = r2 sin
2

b) Rr .
Bài 20: Cho tứ giác ABCD nội tiếp trong đường trịn đường kính AC, BD = a,
CAB  , CAD  .
a) Tính AC. b) Tính diện tích tứ giác ABCD theo a, , .
HD: a) AC =
a
sin( ) 
b)
a
S
2 cos( )
2sin( )
 
 



.
Bài 21: Cho ABC cân đỉnh A, A  , AB = m, D là một điểm trên cạnh BC sao cho
BC = 3BD.
a) Tính BC, AD.
b) Chứng tỏ rằng đường trịn ngoại tiếp các tam giác ABD, ACD là bằng nhau. Tính
cos để bán kính của chúng bằng
1
2
bán kính R của đường trịn ngoại tiếp ABC.
HD: a) BC = m2 sin
2

, AD =
m
5 4cos
3
 b)
11
cos
16
   .
_____________Hết___________
* Learning is the eye of the mind *