Bài tập chương 6 lớp 10

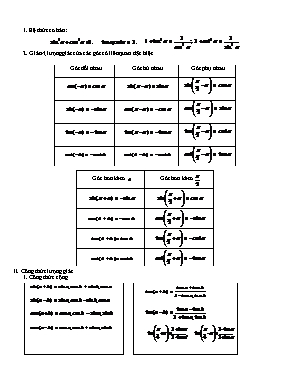
	1. Hệ thức cơ bản:
; 	; 
	2. Giá trị lượng giác của các góc có liên quan đặc biệt
Góc đối nhau
Góc bù nhau
Góc phụ nhau
Góc hơn kém 
Góc hơn kém 
II. Công thức lượng giác
	1. Công thức cộng
	Hệ quả: 
2. Công thức nhân đôi
 Công thức hạ bậc
Công thức nhân ba (*)
	3. Công thức biến đổi tổng thành tích
	4. Công thức biến đổi tích thành tổng
Cho biết một GTLG, tính các GTLG còn lại, với:
	a) 	b) 	
c) 	 	d) 
Cho biết một GTLG, tính giá trị của biểu thức, với:
	a) 	ĐS: 
	b) 	ĐS: 
	c) 	ĐS: 
	d) 	ĐS: 
	e) 	ĐS: 
	g) 	ĐS: 
	h) 	ĐS: 
Cho . Tính giá trị các biểu thức sau:
	a) 	b) 	c) 
	a) Cho . Tính .
	b) Cho . Tính .
Rút gọn các biểu thức sau:
	a) 
	b) 
	c) 
	d) 
Rút gọn các biểu thức sau:
	a) 	ĐS: A = –1
	b) 	ĐS: 
	c) 	ĐS: 
	d) 	ĐS: 
	e) 	ĐS: 
Chứng minh các đẳng thức sau:
	a) 	b) 
	c) 	d) 
	e) 	h) 
 g) f)
	i) 	 k) 
Chứng minh các đẳng thức sau:
	a) 	b) 
	c) 	d) 
	e) 	f) 
	g) 	h) 
	i) 	k) 
Rút gọn các biểu thức sau:
	a) 	 b) 
	c) 	 d) 
	e) 	 f) 
	g) 	 h) 
Chứng minh các biểu thức sau độc lập đối với x:
	a) 	ĐS: 1
	b) 	ĐS: 1
	c) 	ĐS: –2
	d) 	ĐS: 2
Cho tam giác ABC. Chứng minh:
	a) 	b) 	c) 	
d) 	 e) 	
f) g) 	h) 
Tính giá trị của biểu thức lượng giác, khi biết:
	a) 	ĐS: 
	b) 	ĐS: 
c) 	ĐS: 
Cho tam giác ABC. Chứng minh:
a) 	b) 
c) 
d) e) 
f) g) 
h) 
i) 
Tính giá trị của biểu thức lượng giác, khi biết:
a) b) 
c) 
Tính giá trị của biểu thức sau:
a) 	ĐS: 
	b) 	ĐS: 
	c) 	ĐS: 
	d) 	ĐS: 
	e) 	ĐS: 
	f) 	ĐS: 9
	h) 	ĐS: 
Chứng minh các hệ thức sau:
	a) 	b) 
	c) 	d) 
	e) 	f) 
	g) 	h) 
	i) 	k) 
	l) 	m) 
Rút gọn các biểu thức sau:
	a) 	b) 
	c) 	d) 
Chứng minh các đẳng thức sau:
	a) 	b) 
	c) 	d) 
	e) 
	f) 	g) 
Cho tam giác ABC. Chứng minh: 
a) 	b) 
c) d) 
e)f) 
Chứng minh rằng trong tam giác ABC, ta có:
	a) 	b) 
	c) 	d) 
Chứng minh rằng:
	a) Nếu thì tam giác ABC vuông tại A.
	b) Nếu thì tam giác ABC vuông hoặc cân.
	c) Nếu thì tam giác ABC cân.