Bài tập bổ sung Hình lớp 10

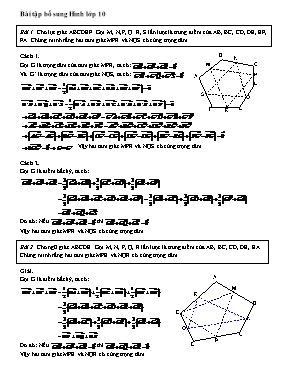
Bài tập bổ sung Hình lớp 10
Bài 1. Cho lục giác ABCDEF. Gọi M, N,P, Q. R, S lần lượt là trung điểm của AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
B
N
M
C
Cách 1.
Gọi G là trọng tâm của tam giác MPR, ta có: 
P
D
A
Và G’ là trọng tâm của tam giác NQS, ta có: 
S
Q
R
F
E
 . Vậy hai tam giác MPR và NQS có cùng trọng tâm.
Cách 2.
Gọi G là điểm bất kỳ, ta có: 
Do đó: Nếu thì . 
Vậy hai tam giác MPR và NQS có cùng trọng tâm.
Bài 2. Cho ngũ giác ABCDE. Gọi M, N, P, Q, R lần lượt là trung điểm của AB, BC, CD, DE, EA. Chứng minh rằng hai tam giác MPE và NQR có cùng trọng tâm.
A
Giải.
M
Gọi G là điểm bất kỳ, ta có: 
R
B
Q
N
E
C
P
D
Do đó: Nếu thì . 
Vậy hai tam giác MPE và NQR có cùng trọng tâm.
Bài 3. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA
. Chứng minh rằng: a) Hai tam giác DMN và BPQ có cùng trọng tâm.
 b) Hai tam giác ANP và CMQ có cùng trọng tâm.
P
N
M
A
B
C
D
Q
B
N
3a/.Gọi G là điểm bất kỳ, ta có: 
M
C
Q
P
A
D
Do đó: Nếu thì . 
Vậy hai tam giác DMN và BPQ có cùng trọng tâm.
3b/.Gọi G là điểm bất kỳ, ta có: 
Do đó: Nếu thì . 
Vậy hai tam giác ANP và CMQ có cùng trọng tâm.
Bài 4. Cho hai hình bình hành ABCD và AB’C’D’ có chung đỉnh A. Chứng minh rằng:
1/ 
2/ Hai tam giác BC’D và B’CD’ có cùng trọng tâm
4.1 Chứng minh: 
D
A
B’
B
D’
C
C’
Ta có: 
4.2 Gọi G là điểm bất kỳ, ta có: 
Do đó: Nếu thì . 
Vậy hai tam giác BC’D và B’CD’ có cùng trọng tâm.
Bài 5. Cho tam giác ABC nội tiếp đường tròn tâm O. H là trực tâm của tam giác ABC và D là trung điểm cạnh BC. G là trọng tâm của tam giác ABC. Chứng minh rằng:
1/ 	2/ 
3/ 	4/ Ba điểm H, O, G thẳng hàng
B
H
B’
D
C
A
O
5.1 Chứng minh: 
H là trực tâm của tam giác ABC, ta có: 
Gọi B’ là điểm đối xứng với điểm B qua tâm O, ta có: 
OD là đường trung bình trong tam giác BB’C, ta có: 
 Tứ giác AHCB’ là hình bình hành 
Từ (1) và (2) 
5.2 Chứng minh: 
Ta có: 
5.3 Chứng minh: 
G là trọng tâm của tam gíc ABC và với điểm H bất ký, ta có: 
Mà 
5.4 Chứng minh: Ba điểm H,O,G thẳng hàng, ta chứng minh: 
G là trọng tâm của tam giác ABC và với điểm O bất ký, ta có:
Mà 
Dó đó: Vậy ba điểm H,O,G thẳng hàng