Bài kiểm tra số 2 - Toán 12 (Mã đề 128)

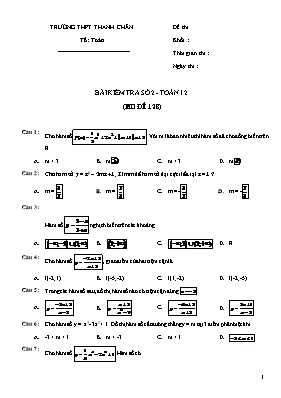
TRƯỜNG THPT THANH CHĂN
Đề thi .......
Tổ: Toán
Khối : ...
Thời gian thi : ..
Ngày thi : .
BÀI KIỂM TRA SỐ 2 - TOÁN 12
 (M· ®Ò 128)
C©u 1 : 
Cho hàmsố:. Với m là bao nhiêu thì hàm số đã cho đồng biến trên R.
A.
m > 3
B.
m3
C.
m < 3
D.
m3
C©u 2 : 
Cho haøm soá y = x3 – 2mx + 1. Tìm m ñeå haøm soá ñaït cöïc tieåu taïi x = 1 ?
A.
m = 
B.
m = 
C.
m = -
D.
m = -.
C©u 3 : 
Hàm số nghịch biến trên các khoảng
A.
B.
C.
D.
R
C©u 4 : 
Cho hàm số , giao điểm của hai tiệm cận là
A.
I(-2;1)
B.
I(-5;-2)
C.
I(1;-2)
D.
I(-2;-5)
C©u 5 : 
Trong các hàm số sau, đồ thị hàm số nào có tiệm cận đứng 
A.
B.
C.
D.
C©u 6 : 
Cho hàm số y = x3- 3x2 + 1. Đồ thị hàm số cắt đường thẳng y = m tại 3 điểm phân biệt khi
A.
-3 < m < 1
B.
m < -3
C.
m > 1
D.
C©u 7 : 
Cho hàm số .Hàm số có
A.
Một cực đại và hai cực tiểu
B.
Một cực tiểu và hai cực đại
C.
Một cực đại và không có cực tiểu
D.
Một cực tiểu và một cực đại
C©u 8 : 
Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số là:
A.
8
B.
6
C.
2
D.
4	
C©u 9 : 
Trên khoảng (0; +¥) thì hàm số :
A.
Có giá trị lớn nhất là Max y = 3
B.
Có giá trị nhỏ nhất là Min y = –1
C.
Có giá trị lớn nhất là Max y = –1
D.
Có giá trị nhỏ nhất là Min y = 3
C©u 10 : 
Cho hàm số . Khẳng định nào sau đây sai:
A.
Hàm số y nghịch biến trên nửa khoảng 
B.
Hàm số y nghịch biến trên 2 khoảng 
C.
Hàm số y nghịch biến trên R
D.
Hàm số y nghịch biến trên nửa khoảng 
C©u 11 : 
Cho hàm số (C) Chọn phát biểu đúng :
A.
Hàm số luôn nghịch biến trên các khoảng xác định
B.
Hàm số luôn đồng biến trên R
C.
Hàm số luôn đồng biến trên các khoảng xác định
D.
Hàm số có tập xác định 
C©u 12 : 
Cho hàm số .Khẳng định nào sau đây đúng?
A.
Đồ thị hàm số không có tiệm cận
B.
Đồ thị hàm số có tiệm cận đứng là x= 1
C.
Đồ thị hàm số có tiệm cận đứng là 
D.
Đồ thị hàm số có tiệm cận ngang là 
C©u 13 : 
Cho hàm số .Toạ độ điểm cực đại của hàm số là
A.
(1;-2)
B.
(3;)
C.
(-1;2)
D.
(1;2)
C©u 14 : 
Đồ thi hàm số nào sau đây có 3 điểm cực trị :
A.
B.
C.
D.
C©u 15 : 
Haøm soá naøo sau ñaây coù cöïc trò
A.
y = x3+ 1
B.
y = x3 – 2x2 +5
C.
y =3x – 5
D.
y =x3+x – 1
C©u 16 : 
Hàmsố: hàm số đồng biến trên R khi
A.
m1
B.
m =1
C.
m 1
D.
C©u 17 : 
Số đường tiệm cận của đồ thị hàm số là
A.
1
B.
3
C.
0
D.
2
C©u 18 : 
Giá trị lớn nhất và nhỏ nhất của hàm số y = x3 - 3x2 - 9x + 1 trên đoạn 
[- 2 ; 4] lần lượt là
A.
6 ; -26
B.
-1 ; -19
C.
4 ; -19
D.
10;-26.
C©u 19 : 
Tiệm cận đứng của đồ thị hàm số là
A.
y = 1
B.
y = -1
C.
x = -1
D.
x = 1
C©u 20 : 
Haøm soá y = x3 + 3x2 – 4 coù giaù trò cöïc ñaïi baèng:
A.
- 4 
B.
0
C.
- 24 
D.
1 
C©u 21 : 
Cho hàm số y = –x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
A.
Hàm số luôn luôn đồng biến;
B.
Hàm số đạt cực tiểu tại x = 1.
C.
Hàm số đạt cực đại tại x = 1;
D.
Hàm số luôn luôn nghịch biến;
C©u 22 : 
Số cực trị của hàm số là:
A.
1
B.
4
C.
3
D.
2
C©u 23 : 
Điểm cực đại của đồ thị hàm số là:
A.
B.
C.
D.
C©u 24 : 
Cho hàm số (C). Tiếp tuyến của (C) tại điểm cực đại có phương trình là:
A.
B.
C.
D.
C©u 25 : 
Hàm số đạt cực tiểu tại x = 2 khi :
A.
B.
C.
D.
C©u 26 : 
Cho hàm số phương trình tiếp tuyến của hàm số tại điểm có hoành độ x0 = 2.
A.
B.
C.
D.
C©u 27 : 
Các khoảng nghịch biến của hàm số là:
A.
B.
C.
R
D.
C©u 28 : 
Hàm số nào sau đây luôn đồng biến trên R
A.
B.
y = x3+3x2– 4 
C.
y = 
D.