50 câu trắc nghiệm môn Số phức

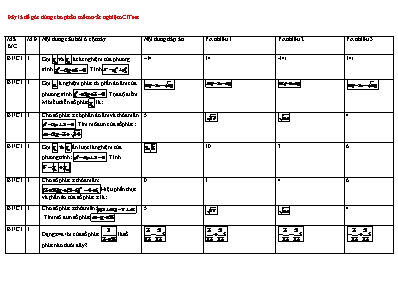
Đây là đề góc dùng cho phần mềm trắc nghiệm CITest
Mã B/C
MĐ
Nội dung câu hỏi ở cột này
Nội dung đáp án
PA nhiễu 1
PA nhiễu 2
PA nhiễu 3
B1/C1
1
Gọi và là các nghiệm của phương trình . Tính 
–14
14
-14i
14i 
B1/C1
1
Gọi là nghiệm phức có phần ảo âm của phương trình . Tọa độ điểm M biểu diễn số phức là:
B1/C1
1
Cho số phức z có phần ảo âm và thỏa mãn . Tìm mô đun của sốphức: 
5 
4
B1/C1
1
Gọi và lần lượt là nghiệm của phươngtrình: . Tính 
10 
3
6 
B1/C1
1
Cho số phức z thỏa mãn: Hiệu phần thực và phần ảo của số phức z là:
0
1
4
6 
B1/C1
1
Cho số phức zthỏa mãn:.Tìm mô đun số phức.
5 
4
B1/C1
1
Dạng z=a+bi của số phức là số phức nào dưới đây?
B1/C1
1
Mệnh đề nào sau đây là sai, khi nói về số phức?
là số thực.
 là số thực
B1/C1
1
Cho số phức . Khi đó môđun của là:
B1/C1
1
Cho số phức . Trong các kết luận sau kết luận nào đúng?
có phần thực và phần ảo đều bằng 0. 
là số thuần ảo. 
Mô đun của bằng 1
.
B1/C1
1
Biểu diễn về dạng của số phức là số phức nào?
B1/C1
1
Điểm biểu diễn số phức có tọa độ là
(-1;-4)
(1;-4)
(1;4)
(-1;4) 
B1/C1
1
Tập hợp nghiệm của phương trình là:
B1/C1
1
Tập nghiệm của phương trình là :
B1/C1
1
 Tìm hai số phức có tổng và tích lần lượt là -6 và 10.
-3-i và -3+i 
-3+2i và -3+8i
-5 +2i và -1-5i
4+4i và 4-4i 
B1/C1
1
Cho số phức và là số phức liên hợp của . Phương trình bậc hai nhận và làm nghiệm là:
B1/C1
1
Cho hai số phức z = a + bi và z’ = a’ + b’i. Số phức có phần thực là:
B1/C1
1
Cho hai số phức z = a + bi và z’ = a’ + b’i. Số phức có phần ảo là: 
B1/C1
1
Trong , cho phương trình bậc hai az2 + bz + c = 0 (*) (a ¹ 0). Gọi D = b2 – 4ac. Ta xét các mệnh đề: 1) Nếu D là số thực âm thì phương trình (*) vô nghiệm 2) Néu D¹ 0 thì phương trình có hai nghiệm số phân biệt 3) Nếu D = 0 thì phương trình có một nghiệm kép Trong các mệnh đề trên: 
Có hai mệnh đề đúng
Có một mệnh đề đúng 
Không có mệnh đề nào đúng
Cả ba mệnh đề đều đúng 
B1/C1
1
Điểm biểu diễn của số phức z = là: 
B1/C1
1
 Số phức nghịch đảo của số phức z = 1 - là: 
 = 
 = 
 = 1 + 
 = -1 + 
B1/C1
1
Số phức z = bằng: 
B1/C1
1
Thu gọn số phức z = ta được: 
z = 
z = 
z = 
z = 
B1/C1
1
Cho số phức z = a + bi. Khi đó số là: 
Một số thực
0
Một số thuần ảo
i 
B1/C1
1
Cho hai số phức z = a + bi và z’ = a’ + b’i. (Trong đó a, b, a’, b’ đều khác 0) điều kiện giữa a, b, a’, b’ để là một số thuần ảo là: 
aa’ + bb’ = 0
a + a’ = b + b’
aa’ - bb’ = 0
a + b = a’ + b’ 
B1/C1
1
Cho số phức z = a + bi. Để z3 là một số thực, điều kiện của a và b là: 
b = 3a
b2 = 5a2 
B1/C1
1
Cho số phức z = a + bi. Để z3 là một số thuần ảo, điều kiện của a và b là: 
b2 = 3a2
ab = 0
B1/C1
1
Cho số phức z = x + yi ¹ 1. (x, y Î R). Phần ảo của số là: 
B1/C1
1
Trong C, phương trình z2 + 4 = 0 có nghiệm là: 
B1/C1
1
Trong C, phương trình có nghiệm là: 
z = 1 + 2i 
z = 3 + 2i
z = 5 - 3i
z = 2 - i
B1/C1
1
Cho phương trình z2 + bz + c = 0. Nếu phương trình nhận z = 1 + i làm một nghiệm thì b và c bằng (b, c là số thực) : 
b = -2, c = 2 
b = 1, c = 3
b = 4, c = 3
b = 3, c = 5
B1/C1
1
Cho phương trình z3 + az2 + bz + c = 0. Nếu z = 1 + i và z = 2 là hai nghiệm của phương trình thì a, b, c bằng (a,b,c là số thực): 
B1/C1
1
Cho số phức z = a + bi ¹ 0. Số phức z-1 có phần thực là: 
a - b
a + b
B1/C1
1
Cho số phức z = a + bi ¹ 0. Số phức có phần ảo là : 
a2 - b2
a2 + b2
B1/C1
1
Tính .
B1/C1
2
 Điểm M biểu diễn số phức có tọa độ là :
M(4;-3)
(3;-4)
(3;4)
(4;3) 
B1/C1
1
 Số phức nào sau đây là số thực:
B1/C1
1
 Biết rằng nghịch đảo của số phức z bằng số phức liên hợp của nó, trong các kết luận sau, kết luận nào đúng.?
z=1
z∈R
z là số thuần ảo.
z=-1 
B1/C1
1
 Nghiệm của phương trình 4+7iz-5-2i=6iz là:
B1/C1
2
 Tìm số phức z biết rằng 
B1/C1
2
Gọi và là các nghiệm của phương trình . Gọi M, N là các điểm biểu diễn của và trên mặt phẳng phức. Khi đó độ dài của MN là:
B1/C1
2
 Gọi và là các nghiệm của phương trình . Gọi M, N, P lần lượt là các điểm biểu diễn của , và số phức trên mặt phẳng phức. Khi đó tập hợp điểm P trên mặt phẳng phức để tam giác MNP vuông tại P là:
Là đường tròn có phương trình , nhưng không chứa M, N. 
Là đường tròn có phương trình 
Đường thẳng có phương trình 
Là đường tròn có phương trình , nhưng không chứa M, N. 
B1/C1
2
 Gọi và là các nghiệm của phương trình . Giá trị của là:
P = 2
P = 1
P = 0
P = 3 
B1/C1
2
 Biết số phức z thỏa phương trình . Giá trị của là:
P = 2
P = 1
P = 0
P = 3 
B1/C1
2
 Tập nghiệm của phương trình là:
B1/C1
3
 Cho số phức z thỏa mãn: . Tìm môđun của . 
8
4 
B1/C1
3
 Tập nghiệm của phương trình : là:
B1/C1
3
 Cho số phức z thỏa mản . Phần thực và phần ảo của z là:
2; -3
2; 3
-2; 3
-2; -3 
B1/C1
39d
 Gọi và là các nghiệm của phương trình . Gọi M, N, P lần lượt là các điểm biểu diễn của , và số phức trên mặt phẳng phức. Để tam giác MNP đều thì số phức k là:
Một đáp số khác. 
B1/C1
3
 Phần thực và phần ảo của là;
0; -1
1; 0
-1; 0
0; 1