5 Dạng toán hàm số lượng giác điển hình - Trần Đình Cư

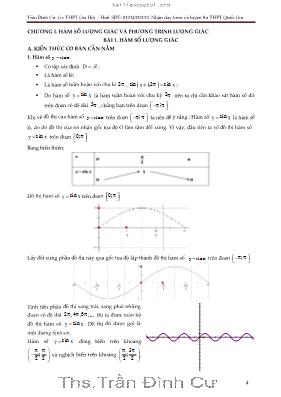
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
4
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
BÀI 1. HÀM SỐ LƯỢNG GIÁC
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Hàm số y sin x
 Cĩ tập xác định D   ;
 Là hàm số lẻ;
 Là hàm số tuần hồn với chu kì 2 ,  sin 2 sinx k x  ;
 Do hàm số siny x là hàm tuần hồn với chu kỳ 2 nên ta chỉ cần khảo sát hàm số đĩ
trên đoạn cĩ độ dài 2 , chẳng hạn trên đoạn ;    .
Khi vẽ đồ thị của hàm số y sin x trên đoạn ;    ta nên để ý rằng : Hàm số siny x là hàm số
lẻ, do đĩ đồ thị của nĩ nhận gốc tọa độ O làm tâm đối xứng. Vì vậy, đầu tiên ta vẽ đồ thị hàm số
siny x trên đoạn 0;  
Bảng biến thiên:
Đồ thị hàm số siny x trên đoạn 0;  
Lấy đối xứng phần đồ thị này qua gốc tọa độ lập thành đồ thị hàm số y sin x trên đoạn ;   
Tịnh tiến phần đồ thị sang trái, sang phải những
đoạn cĩ độ dài 2 ,4 ,6 ,...   thì ta được tồn bộ
đồ thị hàm số siny x . Đồ thị đĩ được gọi là
một đường hình sin.
Hàm số siny x đồng biến trên khoảng
;
2 2
   
  và nghịch biến trên khoảng 3;
2 2
   
  .
8
6
4
2
2
4
6
8
5π 4π 3π 2π π π 2π 3π 4π 5π
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
5
Từ đĩ do tính tuần hồn với chu kì 2 , hàm số siny x đồng biến trên khoảng
        
k2 ; k2
2 2
và nghịch biến trên khoảng 32 ; 2
2 2
k k
    
 
 
2. Hàm số y cosx
 Cĩ tập xác định D   ;
 Là hàm số chẵn;
 Là hàm số tuần hồn với chu kì 2 ;
 Do hàm số osy c x là hàm tuần hồn với chu kỳ 2 nên ta chỉ cần khảo sát hàm số đĩ
trên đoạn cĩ độ dài 2 , chẳng hạn trên đoạn ;    .
Khi vẽ đồ thị của hàm số osy c x trên đoạn ;    ta nên để ý rằng : Hàm số osy c x là hàm
số chẵn, do đĩ đồ thị của nĩ nhận trục Oy làm trục đối xứng. Vì vậy, đầu tiên ta vẽ đồ thị hàm số
osy c x trên đoạn 0;  
Bảng biến thiên:
Đồ thị hàm số osy c x trên đoạn   0;
Lấy đối xứng phần đồ thị này qua trục Oy lập thànhđồ thị hàm số osy c x trên đoạn ;   
Tịnh tiến phần đồ thị sang trái, sang phải những đoạn cĩ độ dài   2 ,4 ,6 ,... thì ta được tồn bộ đồ
thị hàm số osy c x . Đồ thị đĩ được gọi là một đường hình sin
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
6
6
5
4
3
2
1
1
2
3
4
5
6
7π
2
3π 5π
2
2π 3π
2
π π
2
π
2
π 3π
2
2π 5π
2
3π 7π
2
Hàm số y cosx đồng biến trên khoảng  ;0 và nghịch biến trên khoảng  0; . Từ đĩ do tính
tuần hồn với chu kì 2 , hàm số siny x đồng biến trên khoảng     k2 ; k2 và nghịch biến
trên khoảng  2 ; 2k k   .
3. Hàm số y tanx
 Cĩ tập xác định là \ |
2
D k k
     

  ;
 Cĩ tập giá trị là  ;
 Là hàm số lẻ;
 Hàm số tuần hồn với chu kỳ  ,  tan tanx k x  ;
Do hàm số y tan x là hàm tuần hồn với chu kỳ  nên ta chỉ cần khảo sát hàm số đĩ trên đoạn
cĩ độ dài  , chẳng hạn trên đoạn ;
2 2
   
  .
Khi vẽ đồ thị của hàm số y tan x trên đoạn ;
2 2
   
  ta nên để ý rằng : Hàm số y tan x là hàm
số lẻ, do đĩ đồ thị của nĩ nhận gốc tọa độ làm tâm đối xứng. Vì vậy, đầu tiên ta vẽ đồ thị hàm số
tany x trên đoạn    0; 2
Bảng biến thiên:
+∞
1
0
π
2
π
40
y=tanx
x
Đồ thị hàm số tany x trên 0;
2
   

tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
7
Lấy đối xứng phần đồ thị này qua gốc tọa độ lập thành đồ thị hàm số y tan x trên đoạn ;
2 2
   
 
Tịnh tiến phần đồ thị sang trái, sang phải những đoạn cĩ độ dài ,2 ,3 ,...   thì ta được tồn bộ
đồ thị hàm số tany x .
8
6
4
2
2
4
6
8
4π 7π
2
3π 5π
2
2π 3π
2
π π
2
π
2
π 3π
2
2π 5π
2
3π 7π
2
Hàm số tany x đồng biến trên khoảng ;
2 2
   
  . Từ đĩ do tính tuần hồn với chu kỳ  nên
hàm số tany x đồng biến trên khoảng         k ; k2 2 .
Đồ thị hàm số tany x nhận mỗi đường thẳng
2
x k   làm một đường tiệm cận (đứng).
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
8
4. Hàm số y cot x
 Cĩ tập xác định là    D \ k | k  ;
 Cĩ tập giá trị là  ;
 Là hàm số lẻ;
 Hàm số tuần hồn với chu kỳ  ,  cot cotx k x  ;
Do hàm số coty x là hàm tuần hồn với chu kỳ  nên ta chỉ cần khảo sát hàm số đĩ trên đoạn
cĩ độ dài  , chẳng hạn trên đoạn 0;   .
Bảng biến thiên:
-∞
+∞
0
π
π
20
y=cotx
x
Đồ thị hàm số y cot x trên 0;  
Tịnh tiến phần đồ thị sang trái, sang phải những đoạn cĩ độ dài   ,2 ,3 ,... thì ta được tồn bộ đồ
thị hàm số coty x .
8
6
4
2
2
4
6
8
5π
2
2π 3π
2
π π
2
π
2
π 3π
2
2π 5π
2
g x( ) =
1
tan x( )
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
9
Hàm số y cot x nghịch biến trên khoảng  0;  . Từ đĩ do tính tuần hồn với chu kỳ  nên hàm
số y cot x đồng biến trên khoảng  ;k k   .
Đồ thị hàm số coty x nhận mỗi đường thẳng x k  làm một đường tiệm cận (đứng).
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Tìm tập xác định của hàm số
Phương pháp: Để tìm tập xác định của hàm số ta cần lưu ý các điểm sau
  y u x cĩ nghĩa khi và chỉ khi  u x xác định và u(x) 0 .
 u(x)y
v(x)
 cĩ nghĩa khi và chỉ  u x ,  v x xác định và v(x) 0 .
 u(x)y
v(x)
 cĩ nghĩa khi và chỉ  u x ,  v x xác định và v(x) 0 .
 Hàm số y sinx, y cosx  xác định trên  và tập giá trị của nĩ là:
     1 sin x 1 ; 1 cosx 1 .
Như vậy,    y sin u x , y cos u x        xác định khi và chỉ khi  u x xác định.
  y tan u x cĩ nghĩa khi và chỉ khi  u x xác định và  u x k ,k
2
   
  y cot u x cĩ nghĩa khi và chỉ khi  u x xác định và  u x k ,k   .
I. Các ví dụ mẫu
Ví dụ 1. Tìm tập xác định của các hàm số sau :
a)
2
5xy sin
x 1
    
; b) 2y cos 4 x ;  c) y sin x; d) y 2 sin x  .
Giải
a) Hàm số
2
5xy sin
x 1
    
xác định 2x 1 0 x 1.     
Vậy   D \ 1 .
b) Hàm số 2y cos x 4  xác định  2 24 x 0 x 4 2 x 2.       
Vậy  D x | 2 x 2 .    
c) Hàm số y sin x xác định s inx 0 k2 x k2 ,k .         
Vậy  D x | k2 x k2 ,k .         
d) Ta cĩ: 1 sinx 1 2 sinx 0      .
Do đĩ, hàm sĩ luơn luơn xác định hay D .
Ví dụ 2. Tìm tập xác định của các hàm số sau:
a) y tan x
6
    
; b) y cot x ;
3
    
c) sin xy ;
cos(x )
   d)
1y .
tan x 1
 
Giải
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
10
a) Hàm số y tan x
6
    
xác định 2x k x k ,k .
6 2 3
          
Vậy       
2D \ k ,k .
3
 
b) Hàm số y cot x
3
    
xác định x k x k ,k .
3 3
         
Vậy D \ k ,k .
3
      
 
c) Hàm số   
sin xy
cos(x )
xác định   3cos x 0 x k x k ,k .
2 2
              
Vậy 3D \ k ,k .
2
      
 
d) Hàm số 1y
tan x 1
  xác định
x ktan x 1 4 ,k .
cosx 0 x k
2
            

Vậy D \ k , k ;k
4 2
         
 
Ví dụ 3. Tìm tập xác định của các hàm số sau:
a)   1y cos2x ;
cosx
b) 3cos2xy .
sin3x cos3x

Giải
a) Hàm số   1y cos2x
cosx
xác định cosx 0 x k ,k .
2
      
Vậy       D \ k ,k .2 
b) Hàm số 3cos2xy
sin3x cos3x
 xác định 
1 ksin3x cos3x 0 sin6x 0 6x k x ,k .
2 6
       
Vậy kD \ ,k .
6
    
 
Ví dụ 4. Tìm mđể hàm số sau đây xác định trên : y 2m 3cosx. 
Giải
Hàm số đã cho xác định trên R khi và chỉ khi 2m2m 3cosx 0 cosx
3
   
Bất đẳng thức trên đúng với mọi x khi 2m 31 m .
3 2
  
II. Bài tập rèn luyện
BT 1. Tìm tập xác định của các hàm số sau:
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
11
a) 2y 1 cos x  ; b)  
2 sin xy
1 cosx
.
Giải
a) Nhận thấy 20 cos x 1  nên 21 cos x 0, x .   
Vậy D .
b) Hàm số 2 sin xy
1 cosx
  xác định 1 cosx 0 x k2 ,k .        
Vậy      D \ k2 ,k . 
BT 2. Tìm tập xác định của các hàm số sau
1a) y tan 3x ; b)y tan6x ;
3 cot3x
tan2x tan5xc)y cot 3x ; d)y .
sin x 1 6 sin 4x cos3x
      
       
Giải
a) Hàm số y tan 3x
3
    
xác định 53x k x k ,k .
3 2 18 3
          
Vậy 5 kD \ ,k .
18 3
      
 
b) Hàm số 1y tan6x
cot3x
  xác định
cos6x 0
cos6x 0 ksin3x 0 sin12x 0 x ,k .
2sin6x 0
cot3x 0
              

Vậy kD \ ,k .
12
    
 
c) Hàm số       
tan2xy cot 3x
sin x 1 6
xác định khi và chỉ khi
x k2
2sinx 1
kcos2x 0 x ,k .
4 2
ksin 3x 0 x6 18 3
                             

Vậy k kD \ k2 , , ;k .
2 4 2 18 3
              
 
d) Hàm số tan5xy
sin 4x cos3x
  xác định khi và chỉ khi
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
12
kx
10 55x k
cos5x 0 2 4x 3x k2
2sin 4x cos3x cos 4x cos3x
2 4x 3x k2
2
                              
k kx x
10 5 10 5
k27x k2 x ,k
2 14 7
x k2 x k2
2 2
                             

Vậy k k2D \ , , k2 ;k .
10 5 14 7 2
            
 
BT 3. Tìm mđể hàm số sau xác định trên  :
2
3xy .
2sin x msin x 1

 
Giải
Hàm số xác định trên R khi và chỉ khi: 22sin x msin x 1 0   với mọi t 1;1   
Ta cĩ: 2m 8 
 TH 1: 20 m 8 0 2 2 m 2 2         . Khi đĩ  f t 0, t  (thỏa mãn)
 TH 2: 2 m 2 20 m 8 0
m 2 2
         
o Với m 2 2  thì    22f t 2t 2 2t 1 2t 1    
Ta thấy  f t 0 tại 1t 1;1
2
     (khơng thỏa mãn)
o Với m 2 2 thì    22f t 2t 2 2t 1 2t 1    
Ta thấy  f t 0 tại 1t 1;1
2
      (khơng thỏa mãn)
 TH 3: 2 m 2 20 m 8 0
m 2 2
         
khi đĩ tam thức  f t cĩ hai nghiệm phân biệt 1 2t , t (giả
sử 1 2t t )
Ta cĩ bảng xét dấu:
++ - 00
t2t1 +∞-∞
f(t)
t
Từ bảng xét dấu ta thấy:
  2 1f t 2t mt 1 0, t 1,1 t 1           hoặc 2t 1
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
13
Với  2 21 m 4m m 8t 1 1 m 8 m 4 Vô nghiệm4 m 3           
Với  2 22 m 4m m 8t 11 1 m 8 m 4 Vô nghiệm4 m 3                
Vậy giá trị m cần tìm là 2 2 m 2 2.  
Dạng 2. Xét tính chẵn lẻ của hàm số
Phương pháp: Giả sử ta cần xét tính chẵn, lẻ của hàm số y f(x)
 Bước 1: Tìm tập xác định D của hàm số; kiểm chứng D là tập đối xứng qua số 0 tức là
x,x D x D     (1)
 Bước 2: Tính f( x) và so sánh f( x) với f(x)
- Nếu f( x) f(x)  thì f(x) là hàm số chẵn trên D (2)
- Nếu f( x) f(x)   thì f(x) là hàm số lẻ trên D (3)
Chú ý:
- Nếuđiều kiện (1) khơng nghiệm đúng thì f(x) là hàm khơng chẵn và khơng lẻ trên D;
- Nếuđiều kiện (2) v à (3) khơng nghiệmđúng, thì f(x) là hàm khơng chẵn và cũng khơng
lẻ trên D .
Lúc đĩ, để kết luận f(x) là hàm khơng chẵn và khơng lẻ ta chỉ cần chỉ ra điểm 0x D sao
cho 0 0
0 0
f( x ) f(x )
f( x ) f(x )
     
I. Các ví dụ mẫu
Ví dụ 1. Xét tính chẵn, lẻ của các hàm số sau:
a) y = sin2x; b) y = tan x ; c) 4y sin x .
Giải
a) TXĐ: D . Suy ra x D x D     .
Ta cĩ:            f x sin 2x sin2x f x .
Do đĩ hàm số đã cho là hàm số lẻ.
b) TXĐ: D \ k ,k .
2
       
  Suy ra x D x D     .
Ta cĩ:    f x tan x tan x f x     .
Do đĩ hàm số đã cho là hàm số chẵn.
c) TXĐ: D . Suy ra x D x D     .
Ta cĩ:      4 4f x sin x sin x f x     .
Do đĩ hàm số đã cho là hàm số chẵn.
Ví dụ 2. Xét tính chẵn, lẻ của các hàm số sau:
a) y = tanx + cotx; b) y = sinx.cosx.
Giải
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
14
a) TXĐ: kD \ ,k .
2
    
  Suy ra x D x D    
Ta cĩ:                     f x tan x cot x tan x - cot x tan x cot x f x
Do đĩ hàm số đã cho là hàm số lẻ.
b) TXĐ: D  . Suy ra x D x D    
Ta cĩ:        f x sin x .cos x sin x cosx f x       
Do đĩ hàm số đã cho là hàm số lẻ.
Ví dụ 3. Xét tính chẵn, lẻ của các hàm số sau:
a) y = 2sinx + 3; b) y sinx cosx  .
Giải
a) TXĐ: D . Suy ra x D x D    
Ta cĩ:
f 2sin 3 1
2 2
             
; f 2sin 3 5
2 2
            
Nhận thấy
f f
2 2
f f
2 2
                             
Do đĩ hàm số khơng chẵn khơng lẻ.
b) TXĐ: D . Suy ra x D x D    
Ta cĩ: y sinx cosx 2 sin x
4
      
f 2 sin 0; f 2 sin 2
4 4 4 4 4 4
                                 
Nhận thấy
f f
4 4
f f
4 4
                             
Do đĩ hàm số khơng chẵn khơng lẻ.
Ví dụ 4. Xét tính chẵn, lẻ của các hàm số sau:
a)   xy sin2x cos
2
; b)
3
3
cos x 1y .
sin x

Giải
a) TXĐ: D  Suy ra x D x D    
Chọn x D D
4 4
     
Ta cĩ: xf sin cos
3 2 2
      
b) TXĐ:  D \ k ,k    Suy ra x D x D    
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
15
Ta cĩ:       
3 3 3
3 3 3
cos x 1 cos x 1 cos x 1f x f x
sin x sin x sin x
          
Do đĩ hàm số đã cho là hàm số lẻ.
Ví dụ 5. Xác định tham số m để hàm số sau:  y f x 3msin 4x cos2x   là hàm số chẵn.
Giải
TXĐ: D . Suy ra x D x D    
Ta cĩ:
     f x 3msin 4x cos 2x 3msin 4x cos2x       
Để hàm số đã cho là hàm số chẵn thì:
   f x f x , x D 3msin 4x cos2x -3msin 4x cos2x, x D
6msin 4x 0 m 0
         
   
II. Bài tập rèn luyện
BT 1. Xét tính chẵn, lẻ của các hàm số sau:
a) 2y 4x cos5x  ; b) 2y x sinx cot x  .
Giải
a) TXĐ: D  Suy ra x D x D    
Ta cĩ:               2 2f x 4 x cos 5x 4x cos5x f x
Do đĩ hàm số đã cho là hàm số chẵn.
b) TXĐ:  D \ k ,k    Suy ra     x D x D
Ta cĩ:
           2 2 2f x x sin x cot x x sin x cot x x sin x cot x f x             
Do đĩ hàm số đã cho là hàm số chẵn.
BT 2. Xét tính chẵn, lẻ của các hàm số sau:
a) 21y 3sin x
x 3
  ; b) y sin 1 x  .
Giải
a) TXĐ:  D \ 3 .
Ta cĩ: x 3 D   nhưng x 3 D   nên D khơng cĩ tính đối xứng.
Do đĩ, hàm số đã cho khơng chẵn khơng lẻ.
b) TXĐ: D 1; 
Ta cĩ:  x 3 D nhưng x 3 D    nên D khơng cĩ tính đối xứng.
Do đĩ, hàm số đã cho khơng chẵn khơng lẻ.
BT 3. Xét tính chẵn, lẻ của các hàm số sau:
a) y sinx cosx  ; b) tan3x cot 5xy .
sin3x

Giải
a) TXĐ:  D \ 3 .
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
16
Ta cĩ:
3f 3sin 2cos 5 2;
2 2 2
3f 3sin 2cos 5 8
2 2 2
                       
                    
Nhận thấy:    
20;
3
Do đĩ, hàm số đã cho khơng chẵn khơng lẻ.
b) TXĐ:  D \ k ,k .    Suy ra     x D x D
Ta cĩ:
      
   
   
tan 3x cot 5x tan 3x cot 5x
f x f x
sin 3x sin 3x
      
Vậy hàm số đã cho là hàm số chẵn.
BT 4. Tìm tham số a,b để hàm số:
     
3a 1 sinx bcosx, khix 0
y f x
asin x 3 2b cosx, khi x 0
        
là hàm số lẻ.
Giải
TXĐ:  D \ k ,k .    Suy ra x D x D    
 TH 1: Với x 0 thì      f x 3a 1 sin x bcosx
Và          f x asin x 3 2b cos x asin x 3 2b cosx         
Vì hàm số lẻ nên      f x f x hay
   
   
asin x 3 2b cosx 3a 1 sin x bcosx, x 0
2a 1 sin x 3 b cosx 0, x 0
        
      
Đẳng thức trên đúng với mọi x 0 khi
12a 1 0 a .2
3 b 0 b 3
       
 TH 2: Với x 0 thì    f x asin x 3 2b cosx  
Và          f x 3a 1 sin x bcos x 3a 1 sin x bcosx         
Vì hàm số lẻ nên      f x f x hay
   3a 1 sin x bcosx asin x 3 2b cosx      
Đẳng thức trên đúng với mọi x 0 khi
12a 1 0 a .2
3 b 0 b 3
       
Vậy hàm số đã cho lẻ khi 1a ,b 3.
2
 
Dạng 3. Tìm giá trị lớn nhất và và giá trị nhỏ nhất của hàm số lượng giác
Phương pháp: Cho hàm số y f(x) xác định trên tập D
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
17
        D 0 0
f(x) M, x D
M max f(x)
x D : f(x ) M

D 0 0
f(x) m, x D
m min f(x)
x D : f(x ) m
       
Lưu ý:
 1 sinx 1; 1 cosx 1.     
 2 20 sin x 1; 0 cos x 1.   
 0 sin x 1; 0 cosx 1.   
I. Các ví dụ mẫu
Ví dụ 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y 2sin x 1
4
      ; b) y 2 cosx 1 3   .
Giải
a) Ta cĩ:
1 sin x 1 2 2sin x 2 1 2sin x 1 3
4 4 4
                               
Hay 1 y 3   . Suy ra:
Maxy 3 khi sin x 1 x k2 ,k .
4 4
          

Miny 1  khi 3sin x 1 x k2 ,k .
4 4
            

b) Ta cĩ:
1 cosx 1 0 cosx 1 2 0 cosx 1 2
0 2 cosx 1 2 2 3 2 cosx 1 3 2 2 3
          
          
Hay    3 y 2 2 3 Suy ra
Maxy 2 2 3  khi cosx 1 x k2 ,k .    
Miny 3  khi cosx 0 x k ,k .
2
     
Ví dụ 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a)  y sinx cosx ; b) y 3 sin2x cos2x  .
Giải
a) Ta cĩ:       y sinx cosx 2 sin x 4 2 y 2   .
Suy ra:
Maxy 2 khi sin x 1 x k2 ,k .
4 4
          

Miny 2  khi             
3sin x 1 x k2 ,k .
4 4

tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
18
b) Ta cĩ: 3 1y 3 sin2x cos2x 2 sin2x cos2x 2sin 2x
2 2 6
               
Suy ra:   2 y 2 . Do đĩ:
Maxy 2 khi sin 2x 1 2x k2 x k2 ,k .
6 6 2 3
                

Miny 2  khi                    sin 2x 1 2x k2 x k2 ,k .6 6 2 6 
Ví dụ 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) 2y cos x 2sin x 2   ; b) 4 2y sin x 2cos x 1   .
Giải
a) Ta cĩ:
 
 
22 2
22
y cos x 2sin x 2 1 sin x 2sin x 2
sin x 2sin x 3 sin x 1 4
      
       
Vì  21 sinx 1 2 sin x 1 0 4 sin x 1 0           
   2 24 sin x 1 0 0 sin x 1 4 4          
Hay 0 y 4 
Do đĩ:
Maxy 4 khi sin x 1 x k2 ,k .
2
     
Miny 0 khi sin x 1 x k2 ,k .
2
       
Lưu ý:
Nếu đặt t sin x,t 1;1     . Ta cĩ (P):   2y f t t 2t 3     xác định với mọi
t 1;1    , (P) cĩ hồnh độ đỉnh t 1 và trên đoạn 1;1   hàm số đồng biến
nên hàm số đạt giá trị nhỏ nhất tại t 1 hay sin x 1    và đạt giá trị lớn
nhất khi t 1 hay sin x 1  .
b) Ta cĩ
 
 
24 2 2 2
24 2 2
y sin x 2cos x 1 1 cos x 2cos x 1
cos x 4cos x 2 cos x 2 2
      
     
Vì  22 2 20 cos x 1 2 cos x 2 1 4 cos x 2 1           
 222 cos x 2 2 1 2 y 1         
Do đĩ:
Maxy 2 khi
tailieucuatui.org
Trần Đình Cư. Gv THPT Gia Hội - Huế. SĐT: 01234332133. Nhận dạy kèm và luyện thi THPT Quốc Gia
19
2cos x 0 cosx 0 x k ,k .
2
       
Miny 1  khi
2cos x 1 sin x 0 x k ,k .      
Lưu ý:
N