300 câu hỏi trắc nghiệm môn Toán học 12

300 CÂU HỎI TRẮC NGHIỆM MÔN TOÁN 12 
Phần 1: 100 CÂU 
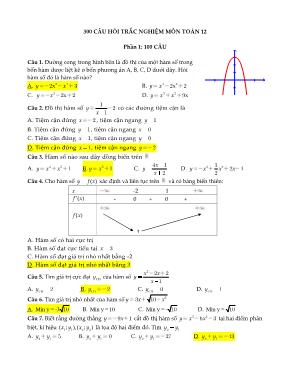
Câu 1. Đường cong trong hình bên l| đồ thị của một h|m số trong 
bốn h|m được liệt kê ở bốn phương {n A, B, C, D dưới đ}y. Hỏi 
h|m số đó l| h|m số n|o? 
A. 2 42 3xy x B. 4 22 2xy x 
C. 2 2 2xy x D. 3 2 9xy x x 
Câu 2. Đồ thị h|m số 
1
2
1
y
x
 có c{c đường tiệm cận l| 
A. Tiệm cận đứng 2x , tiệm cận ngang 1y 
B. Tiệm cận đứng 1y , tiệm cận ngang 0x 
C. Tiệm cận đứng 1x , tiệm cận ngang 0y 
D. Tiệm cận đứng 1x , tiệm cận ngang 2y 
Câu 3. H|m số n|o sau đ}y đồng biến trên 
A. 4 2 1y x x B. 3 1y x C. 
4 1
2
x
y
x
 D. 3 2
1
2 1
2
y x x x 
Câu 4. Cho h|m số ( )y f x xác định v| liên tục trên v| có bảng biến thiên: 
x -2 1 
'( )f x - 0 + 0 + 
( )f x 
A. H|m số có hai cực trị 
B. H|m số đạt cực tiểu tại 3x 
C. H|m số đạt gi{ trị nhỏ nhất bằng -2 
D. H|m số đạt gi{ trị nhỏ nhất bằng 3 
Câu 5. Tìm gi{ trị cực đại 
CD
y của h|m số 
2 2 2
1
x x
y
x
A. 
CD
2y B. 
CD
2y C. 
CD
0y D. 
CD
1y 
Câu 6. Tìm gi{ trị nhỏ nhất của h|m số 23 10y x x 
A. Min y = -3 10 B. Min y =10 C. Min y = - 10 D. Min y = 10 
Câu 7. Biết rằng đường thẳng 9 1y x cắt đồ thị h|m số 3 26 3y x x tại hai điểm ph}n 
biệt, kí hiệu 1 1 2 2( ; ),( ; )x y x y l| tọa độ hai điểm đó. Tìm 2 1y y 
A. 2 1 5y y B. 2 1 0y y C. 2 1 27y y D. 2 1 43y y 
3 
-2 -1 1 2
-1
1
2
3
x
y
Câu 8. Cho h|m số 3 26 3 2 6( )y x x m x m . Gi{ trị n|o của m để h|m số có hai cực trị 
1 2,x x thỏa điều kiện 
3 3
1 2 28x x 
A. 3m B. 2m C. 1m D. 0m 
Câu 9. Tìm m để đường thẳng 4y m cắt đồ thị h|m số (C) 4 28 3y x x tại 4 điểm ph}n 
biệt. 
A. 
13 3
4 4
m B. 
3
4
m C. 
13
4
m D. 
13 3
4 4
m 
Câu 10. Cho h|m số 
2 3
1
mx
y
x
.Với gi{ trị n|o của m thì dường tiệm cận đứng, tiệm cận 
ngang cùng với hai trục tọa độ tạo th|nh hình chữ nhật có diện tích bằng 10 
A. 2m B. 5m C. 5m D. 
1
5
m 
Câu 11. Cho 
12
1 1
2 2 1 2
y y
P x y
x x
. Biểu thức rút gọn của P là: 
A. x B. 2x C. 1x D. 1x 
Câu 12. Giải phương trình 23 8 3 7 0.
x
x 
A. 
3
0
7log
x
x
 B. 
3
0
49log
x
x
 C. 
3
0
1
7
2
log
x
x
 D. 
3
1
49log
x
x
Câu 13. Hàm số 2 6 9loga ay x nghịch biến trên khoảng 0; khi: 
A. 
3
4 2
a
a
 B. 
3
4 2
a
a
 C. 
3
4 2
a
a
 D. 
3
4 2
a
a
Câu 14. Tập nghiệm của bất phương trình 21
2
3 2 1log ( )x x là: 
A. 0 1 2 3; ; B. 0 3; C. 0 3; D. 0 3; ; 
Câu 15. Tập x{c định của h|m số 2 9 1 3lny x x là 
A. 10 1; ; B. 10 1; C. 10 1; ; D. 10 1; ; 
Câu 16. Cho 2 5log m ; 3 5log n . Khi đó 6 5log tính theo m , n là : 
A. 
2
m n
 B. 
m n
m n
 C. 2 2m n D. 
.m n
m n
Câu 17. Tìm mệnh đề đúng trong c{c mệnh đề sau: 
A. H|m số 
3
2
x
y đồng biến trên khoảng ; 
B. . H|m số 5
x
y nghịch biến trên khoảng ; 
C. Đồ thị c{c h|m số 4xy và 4logy x đối xứng nhau qua đường ph}n gi{c y x 
D. . H|m số 
x
y luôn đi qua điểm 1 0; 
Câu 18. Tìm m để phương trình 2 22 2 5log logx x m có nghiệm 1 8;x 
A. 4 5;m B. 5 8;m C. 3 8;m D. 4 8;m 
Câu 19. Tính đạo h|m của 10xy 
A. 110' . xy x B. 10 10' .lnxy C. 10' xy D. 
10
10
'
ln
x
y 
Câu 20. Một người gửi tiết kiệm với lãi suất 7,2%/năm v| lãi h|ng năm được nhập v|o vốn. 
Hỏi sau bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu 
A. 7 B. 8 C. 9 D. 10 
Câu 21. Tìm nguyên h|m của h|m số 2
2
3x x dx
x
A. 2 3 3
2 2
3 2
3
lnx x dx x x x C
x
 B. 2 3 3
2 2
3 2
3
lnx x dx x x x C
x
C. 2 3 3
2 2
3 2
3
lnx x dx x x x C
x
D. 2 3 3
2 2
3 2
3
lnx x dx x x x C
x
Câu 22. Gi{ trị của m để h|m số 3 21 2 1 3 4( ) ( ) ( )F x m x m x x l| một nguyên h|m của 
h|m số 26 2 3( )f x x x là 
A. 4m B. 0m C. 1m D. 3m 
Câu 23. Tính tích phân 
1
0
xI xe dx 
A. 1 B. 1e C. -1 D. 1e 
Câu 24. Tính diện tích hình phẳng giới hạn bởi đồ thị h|m số 3 1y x , đường thẳng 2x , 
trục ho|nh v| trục tung. 
A. 
3
2
 B. 
5
2
 C. 
9
2
 D. 
7
2
Câu 25. Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi đường thẳng 
2y x v| đồ thị h|m số 2y x là 
A. 
4
3
 B. 
3
2
 C. 
5
3
 D. 
23
15
Câu 26. Giả sử 
5
1
2 1
ln
dx
c
x
. Gi{ trị của c là: 
A. 9 B. 3 C. 81 D. 8 
Câu 27. Gi{ trị của 
2
2
0
2 xe dx là: 
 A. 4e B. 4 1e C. 44e D. 43 1e 
Câu 28. Kí hiệu (H) l| hình phẳng giới hạn bởi đồ thị h|m số 22y x x và 0y . Tính thể 
tích vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox 
A. 
16
15
 B. 
17
5
 C. 
18
5
 D. 
19
5
Câu 29. Cho số phức 5 3Z i . Tìm phần thực v| phần ảo của số phức 2Z 
A. Phần thực bằng 10 v| phần ảo bằng 6 B. Phần thực bằng 10 v| phần ảo bằng 6i 
C. Phần thực bằng 10 v| phần ảo bằng 6 D. Phần thực bằng 10 v| phần ảo bằng 6i 
Câu 30. Cho hai số phức 1 3Z i và 2 1 2Z i . Tính môđun của số phức 1 22Z Z 
A. 17 B. 7 C. 5 D. 34 
Câu 31. Trong mặt phẳng Oxy , điểm 1 3( ; )M biểu diễn cho số phức Z thỏa điều kiện n|o 
trong c{c điều kiện sau đ}y: 
A. 2 1 4 3 5( )Z i i B. 2 5 5i Z i 
C. 3 2 1 4 1( )Z i i D. 2 3 5 5 8
1
( )
Z
i i
i
Câu 32. Trong mặt phẳng Oxy , gọi M l| điểm biểu diễn cho số phức 3 4Z i ; 'M l| điểm 
biểu diễn cho số phức 
2 8 6( )
'
i
Z
Z
. Tính diện tích tam gi{c 'OMM 
A. 4 B. 9 C. 6 D. 12 
Câu 33. Trong mặt phẳng Oxy , tìm tập hợp điểm biểu diễn số phức Z thỏa mãn 
2 3( )Z i i Z 
A. Đường tròn t}m 
2
0
9
;I bán kính 
2 2
3
R 
B. Đường tròn t}m 
2
0
9
;I bán kính 
2 3
3
R 
C. Đường tròn t}m 
2
0
9
;I bán kính 
2 3
2
R 
D. Đường tròn t}m 
2
0
9
;I bán kính 
2 2
3
R 
Câu 34. Kí hiệu 1Z , 2Z l| c{c nghiệm phức của phương trình 
2 2 6 0Z Z . Tính gi{ trị biểu 
thức 
2 2
1 2A Z Z 
A. 2 6 B. 2 C. 6 D. 12 
C}u 35. Một hình lập phương có tổng diện tích tất cả c{c mặt bằng 212a . Thể tích của khối lập 
phương bằng: 
A. 34a B. 32 2a C. 32a D. 3a 
C}u 36. Cho khối chóp tam gi{c S.ABC có đ{y l| tam gi{c đều cạnh a. Đường cao SA, góc 
giữa SB v| mặt phẳng (ABC) bằng 450. Tính thể tích V của khối chóp S.ABC. 
 A. 
3 3
12
a
V B. 
3 3
4
a
V C. 
3 6
12
a
V D. 
3
3
a
V 
C}u 37. Cho khối lăng trụ ABCD.A’B’C’D’ có đ{y l| hình vuông cạnh a , AA’ bằng 3a . Góc 
giữa cạnh bên A’A v| mặt phẳng (ABCD) bằng 600. Tính thể tích V của khối lăng trụ theo a . 
A. 
3
2
a
 B. 3 3a C. 
33
2
a
 D. 33a 
C}u 38. Một hình chóp S.ABC có thể tích bằng 
34
3
a
. Tính khoảng c{ch d từ S đến mặt phẳng 
(ABC), biết SA = SB = SC v| SA, SB, SC đôi một vuông góc với nhau. 
A. 
2 3
3
d a B. 
3
3
d a C. 2 3d a D. 
3
6
d a 
C}u 39. Một mặt phẳng đi qua trục của hình nón cắt hình nón theo thiết diện l| tam gi{c đều 
cạnh 4 m. Tính 
xq
S của hình nón. 
A. 216 ( )
xq
S m B. 2
4
3
( )
xq
S m C. 24 ( )
xq
S m D. 28 ( )
xq
S m 
C}u 40. Cho hình vuông ABCD cạnh a. Gọi I, J lần lượt l| trung điểm của AB v| CD. Quay 
hình vuông ABCD quanh trục IJ sinh ra một hình trụ. Tính thể tích V của hình trụ đó. 
A. 
3
4
a
V B. 
3
2
a
V C. 
3
4
a
V D. 3V a 
C}u 41. Cho hình chóp S.ABCD có đ{y l| hình vuông cạnh bằng 4. Tam gi{c SAB đều v| nằm 
trong mặt phẳng vuông góc với mặt phẳng đ{y. Tính diện tích S của mặt cầu ngoại tiếp hình 
chóp S.ABCD. 
A. 
24
3
S B. 
56
3
S C. 
112
3
S D. 
7
3
S 
C}u 42. Một miếng tôn hình chữ nhật có chiều d|i 98 (cm), chiều rộng 30 (cm) được uốn 
th|nh mặt xung quanh của một thùng đựng nước hình trụ có đường sinh bằng 30 (cm), biết 
rằng chỗ mối ghép mất 2 (cm). Thùng đựng được bao nhiêu lít nước. 
A. 20 lít B. 22 lít C. 25 lít D. 30 lít 
C}u 43. Trong không gian với hệ trục tọa độ Oxyz . Cho mặt phẳng (P) vuông góc với đường 
thẳng 
1 2
1
2
:
x t
d y t
z
. Vectơ n|o dưới đ}y l| vectơ ph{p tuyến của (P)? 
A. 1 2 1 2( ; ; )n B. 2 2 1 2( ; ; )n C. 3 1 2 0( ; ; )n D. 4 2 1 0( ; ; )n 
C}u 44. Trong không gian với hệ trục tọa độ Oxyz . Cho mặt cầu (S) có phương trình 
2 2 2 2 4 2 0x y z x y z . Tìm tọa độ t}m I v| b{n kính R của (S). 
A. 1 2 1 6( ; ; );I R B. 1 2 1 6( ; ; );I R C. 1 2 1 6( ; ; );I R D. 
1 2 1 6( ; ; );I R 
C}u 45. Trong không gian với hệ trục tọa độ Oxyz . Cho mặt phẳng 2 2 0( ) : x y z và 
mặt phẳng 2 2 9 0( ) : x y z . Tính khoảng c{ch d giữa và . 
A. 9d B. 3d C. 6d D. 1d 
C}u 46. Trong không gian với hệ trục tọa độ Oxyz . Hình chiếu vuông góc của 1 0 2( ; ; )A trên 
mặt phẳng (P) 4 0x y z là: 
A. 1 0 2 2( ; ; )A B. 1 0 1 3( ; ; )A C. 1 4 1 1( ; ; )A D. 
1 2 1 1( ; ; )A 
C}u 47. Trong không gian với hệ trục tọa độ Oxyz . Cho mặt cầu (S) có phương trình 
2 2 2 2 4 1 0zx y z y v| hai điểm A(2;2;0) v| B(2;1;0). Có bao nhiêu mặt phẳng đi qua 
A, B v| tiếp xúc với (S)? 
A. 1 B. 2 C. 3 D. 4 
C}u 48. Trong không gian với hệ trục tọa độ Oxyz . Cho mặt phẳng (P) có phương trình 
2 2 1 0zx y . Gọi , , lần lượt l| góc hợp bởi mặt phẳng (P) với c{c mp(Oxy), 
mp(Oyz) v| mp(Oxy). Khi đó 
A. 2 2 2 3cos cos cos B. 2 2 2 2cos cos cos 
C. 2 2 2 1sin sin sin D. 
2 2 2 2sin sin sin 
C}u 49. Trong không gian với hệ trục tọa độ Oxyz . Cho ba điểm A(2;0;-1), B(1;-2;3) và 
C(0;1;2). Có bao nhiêu mặt phẳng đi qua gốc tọa độ v| c{ch đều ba điểm A, B và C? 
A. 1 B. 2 C. 3 D. 4 
C}u 50. Trong không gian với hệ trục tọa độ Oxyz . Cho mặt phẳng (P) v| (Q) lần lượt có 
phương trình 0x y z và 1 0x y . Phương trình đường thẳng d l| giao tuyến của 
hai mặt phẳng (P) v| (Q) có phương trình: 
A. 1
x t
y t
z t
 B. 1
1
x t
y t
z
 C. 
1
1
1
x t
y t
z
 D. 
3
4
2
x t
y t
z
Câu 51: Đường cong trong hình bên l| đồ thị của một h|m số n|o 
trong bốn h|m số được liệt kê ở bốn phương {n A, B, C, D dưới đ}y. 
Hỏi h|m số đó l| h|m số n|o? 
A. 3 23 1y x x B. 3 1y x x 
C. 3 1y x x D. 3 23 9 1y x x x 
Câu 52: Tìm khoảng đồng biến của h|m số 3 3 2y x x ? 
A. 1 1( ; ) B. 1 1( ; ); ( ; ) 
C. 1 1( ; ) ( ; ) D. 1 2( ; ); ( ; ) 
Câu 53: Cho h|m số ( )y f x có đạo h|m cấp hai trên khoảng ( ; )a b ; 0 ( ; )x a b và 
0 00 0( ) , ( )f x f x . Khẳng định n|o sau đ}y l| khẳng định đúng? 
A. Điểm 0x l| điểm cực tiểu của h|m số ( )y f x . 
B. Gi{ trị 0( )f x l| gi{ trị cực đại của h|m số ( )y f x . 
C. Điểm 0x l| điểm cực đại của đồ thị h|m số ( )y f x . 
D. Điểm 0 0( ; )M x y l| điểm cực đại của h|m số ( )y f x 
Câu 54: Cho hàm số ( )y f x x{c định trên khoảng 0( ; ) v| có bảng biến thiên như sau: 
x 0 1 
y - 0 + 
y 
 -3 
Khẳng định n|o sau đ}y l| khẳng định đúng? 
A. H|m số có gi{ trị nhỏ nhất l| 1. 
B. H|m số có gi{ trị nhỏ nhất l| -3. 
C. H|m số chỉ có gi{ trị cực tiểu nhưng không có gi{ trị nhỏ nhất. 
D. H|m số có gi{ trị nhỏ nhất l| 0. 
Câu 55: Tìm gi{ trị cực đại 
CĐ
y của h|m số 4 22 2017y x x ? 
A. 0
CĐ
y B. 1
CĐ
y C. 2017
CĐ
y D. 2016
CĐ
y 
Câu 56: Tìm gi{ trị lớn nhất của h|m số 4 22 1y x x trên đoạn 2 2; ? 
A. 2 B. 1 C. 0 D.9 
Câu 57: Tìm c{c tiệm cận đứng v| ngang của đồ thị h|m số 
2
2
2 3 1
1
x x
y
x
 ? 
A. 1 2;x y B. 1 2;x y C. 2 1;x y D. 
2 1;x y 
Câu 58: Biết rằng đường thẳng 3 5y x cắt đồ thị h|m số 3 4 5y x x tại điểm duy 
nhất; kí hiệu 0 0( ; )x y l| tọa độ của điểm đó. Tìm 0 02017x y . 
A. 3 B. 0 C. -5 D. 2017 
Câu 59: Tìm m để đồ thị h|m số 2 3 23 3 6y m x mx mx đi qua điểm 2 8( ; )M . 
A. 1m B. 
1
4
m C. 
1
1
4
m m D. 
1
1
4
m m 
Câu 60: Tìm m để h|m số 
2 1
2
m x
y
x
 đạt gi{ trị nhỏ nhất trên đoạn [-3;-1] bằng 1. 
A. 1m B. 2m C. 2m D. 1 3m m 
Câu 61: Một đo|n xe khởi h|nh từ bến C chở h|ng cứu trợ đến chốt M trên tuyến đường AB, 
từ đó h|ng sẽ được chuyển cho một xã D bị chia cắt bởi lũ lụt (như hình vẽ). Hỏi cần đặt chốt 
M ở vị trí n|o trên AB sao cho tổng khoảng c{ch từ C đến D qua M l| ngắn nhất, với giả sử 
chốt M có thể đặt bất cứ vị trí n|o trên tuyến đường AB v| 
20 48 60; ;AC km AB km BD km . 
A. 16 22;AM km BM km 
B. 12 36;AM km BM km 
C. 8 40;AM km BM km 
D. 24 24;AM km BM km 
Câu 62: Giải phương trình: 
2 6 8 12
2
x x 
A. 2x B. 3x C. 2x D. 3x 
Câu 63: Tìm tập x{c định của h|m số 2 3( )y x x 
A. 0 1( ; ) B. 0 1( ; ) ( ; ) C. R D. 0 1;R 
Câu 64: Giải bất phương trình 
1
3 5
5 3
x
A. 2x B. 2x C. 2x D. 2x 
Câu 15: Tính đạo h|m của h|m số 2 1xy e 
A. 22 1( ) xy x e B. 2 1
1
2
xy e C. 2 12 xy e D. 2 1xy e 
Câu 66: Trong c{c h|m số sau, h|m số n|o nghịch biến trên R? 
A. 
3
x
y B. 
5
3
x
y
e
 C. 
3x
y D. 
1
2 2
x
y 
Câu 67: Cho h|m số 2017xy e . Tính gi{ trị của 2(ln )y ? 
A. 2019 B. 2019e C. 20172e D. 2017 e 
Câu 68: Khẳng định n|o sau đ}y sai? 
A. 
1
1xe x
e
B. H|m số 2logy x x{c định khi 0x 
C. Đồ thị h|m số 3xy và 
1
3
x
y đối xứng nhau qua trục tung. 
D. Đồ thị h|m số 3logy x và 1
3
logy x đối xứng nhau qua trục tung. 
Câu 69: Biết 2 3log , loga b . Tính 4 0 12log , theo a và b. 
A. 
2 2
4
a b
 B. 
2 2
4
a b
 C. 
2 2
4
a b
 D. 
2 2
4
a b
Câu 70: Cho h|m số 
1
xe
y
x
. Chọn khẳng định đúng trong c{c khẳng định sau? 
A. 0 0y x B. 0 0y x C. 0 1y x D. 0 1y x 
Câu 71: Một người gởi tiết kiệm với lãi suất 7,5% một năm, lãi suất h|ng năm được nhập v|o 
vốn v| người n|y không rút lãi trong suốt qu{ trình gởi. Hỏi sau khoảng bao nhiêu năm thì 
người gởi n|y sẽ nhận được gấp đôi số tiến ban đầu, giả sử lãi suất không đổi trong suốt qu{ 
trình gởi tiết kiệm? 
A. 5 năm B. 16 năm C. 21 năm D. 11 năm 
Câu 72: Viết công thức tính diện tích S của hình thang cong giới hạn bởi đồ thị (C) h|m số 
( )y f x , trục ho|nh v| c{c đường thẳng ; ( )x a x b a b . 
A. ( )
b
a
S f x dx B. ( )
b
a
S f x dx C. 
2
( )
b
a
S f x dx D. ( )
a
b
S f x dx 
Câu 73: Tìm nguyên h|m của h|m số 2( ) sinf x x 
A. 
1
2
( ) cos2 +Cf x dx x B. ( ) cos2 +Cf x dx x 
C. 
1
2
( ) cos2 +Cf x dx x D. ( ) cos2 +Cf x dx x 
Câu 74: Kí hiệu (H) l| hình phẳng giới hạn bởi đồ thị h|m số 21y x v| trục ho|nh. Tính 
thể tích vật thể tròn xoay được sinh ra khi quay (H) xung quanh trục Ox. 
A. 
16
15
V B. 
16
15
V C. 
4
3
V D. 
4
3
V 
Câu 75: Giả sử h|m số ( )y f x liên tục trên khoảng K v| , ,a b c K . Khẳng định n|o sau đ}y 
l| khẳng định sai? 
 A. 0( )
a
a
f x dx B. ( ) ( )
b a
a b
f x dx f x dx 
C. ( ) ( ) ( ) , ( ; )
b b c
a c a
f x dx f x dx f x dx c a b D. ( ) ( )
b b
a a
f x dx f t dt 
Câu 76: Tính tích phân 
2
0
cosI x xdx 
A. 1
2
I B. 
2
I C. 1
2
I D. 1
2
I 
Câu 77: Tính diện tích hình phẳng giới hạn bởi đồ thi hai h|m số 3 3 2y x x và 
2 2y x x 
A. 
8
3
 B. 
9
4
 C. 
19
6
 D. 
37
12
Câu 78: Gọi H l| hình phẳng giới hạn bởi c{c đường: 0sin ; ; ;y x Ox x x . Quay H 
xung quanh trục Ox ta được khối tròn xoay có thể tích l|: 
A. 
2
 B. 
2
2
 C. D. 2 
Câu 79: Cho phương trình bậc hai 2 0 1( )ax bx c với 0, , ,a b c R a và 2 4b ac . Khi 
đó, công thức n|o l| công thức nghiệm của phương trình (1) với 0? 
A. 1 2 2,
b
x
a
 B. 1 2 2,
b i
x
a
C. 1 2 2,
b i
x
a
 D. 1 2 2,
b i
x
a
Câu 80: Cho số phức 2 3z i . Tìm số phức liên hợp của z. 
A. 3 2z i B. 2 3z i C. 2 3z i D. 2 3z i 
Câu 81: Cho số phức 4 2z i . Tính môđun của số phức z. 
A. 20z B. 12z C. 2 5z D. 2z 
Câu 82: Cho hai số phức 1 21 2 3;z i z i . Tìm phần thực của số phức 1 23z z z 
A. -1 B. 10 C. 101 D. -i 
Câu 83: Cho số phức 1 2z i . Hãy tìm một phương trình bậc hai với hệ số thực nhận z và 
z l|m nghiệm. 
A. 2 2 5 0x x B. 2 2 5 0x x C. 2 4 5 0x ix D. 2 2 3 0x x 
Câu 84: Một học sinh thực hiện đẩy tạ trong giờ thể dục. Quỹ đạo của quả tạ l| một đường 
cong parabol trong mặt phẳng Oxy có phương trình 2 4y x x v| vị trí của quả tạ được 
xem l| một điểm (như hình vẽ bên dưới). Khi đó, vị trí cao nhất của quả tạ l| điểm biểu diễn 
của số phức n|o sau đ}y? 
A. 2 4z i B. 2 4z i C. 2 4z i D. 
2 4z i 
Câu 85: Tính thể tích V của một khối tứ diện đều cạnh a? 
A. 
3 2
12
a
V B. 
3 3
6
a
V C. 
3 2
4
a
V D. 
3 3
12
a
V 
Câu 86: Tính thể tích V khối hộp chữ nhật .ABCD A B C D , biết rằng 
2 3; ;AB a AD a AA a . 
A. 37V a B. 375V a C. 36V a D. 32V a 
Câu 87: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc nhau v| 
3 5;OA a AB OC a . Gọi M, N, P lần lượt l| trung điểm của OA, OB, OC. Tính thể tích V 
của khối chóp OMNP. 
A. 310V a B. 
35
2
a
V C. 35V a D. 
35
4
a
V 
Câu 88: Người ta muốn x}y một bồn chứa nước dạng khối hộp chữ nhật có hai mặt dựa v|o 
hai bức tường vuông góc nhau có sẵn. Biết chiều d|i, chiều rộng v| chiều cao của bồn lần lượt 
l| 6m, 2m, 3m (như hình vẽ). Biết mỗi viên gạch có chiều d|i 20cm, chiều rộng 10cm, chiều 
cao 5cm. Hỏi thể tích thực của bồn sau khi x}y l| bao nhiêu? (giả sử lượng vữa x}y l| không 
đ{ng kể). 
A. 336m B. 333 63, m C. 331 26, m D. 333 6, m 
Câu 89: Cắt một khối trụ bởi một mặt phẳng song song với trục thì thiết diện nhận được l| 
hình gì? 
A. Hình vuông B. Hình chữ nhật C. Hình tròn D. Hình trụ 
Câu 90: Cho hình lập phương .ABCD A B C D có cạnh bằng a. Tính b{n kính r của mặt cầu 
ngoại tiếp hình lập phương .ABCD A B C D . 
A. 
5
2
a
r B. 3r a C. 
3
2
a
r D. 5r a 
Câu 91: Cắt một hình nón đỉnh S bởi một mặt phẳng đi qua trục ta nhận được một tam gi{c 
vuông c}n có cạnh huyền bằng 2a . Tính diện tích xung quanh 
xq
S của khối nón tương ứng. 
A. 2 2
xq
S a B. 
2 2
2xq
a
S 
C. 
2 2
6xq
a
S D. 
2 1 2
2xq
a
S 
Câu 92: Một quả bóng tennis hình cầu được đặt tiếp xúc với tất cả c{c mặt của một c{i hộp 
hình lập phương. Tính tỉ số thể tích của quả bóng v| thể tích của hộp? 
A. 
6
6
 B. 
2
 C. 
4
3
 D. 
6
Câu 93: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng (d): 
11 2
5 3 1
yx z
. 
Vectơ n|o dưới đ}y l| một vectơ chỉ phương u của (d)? 
A. 1 1 2( ; ; )u B. 5 3 1( ; ; )u C. 1 1 2( ; ; )u D. 1 3 5( ; ; )u 
Câu 94: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng (d): 
2
3
2
( )
x t
y t t R
z t
. Viết 
phương trình mặt phẳng (P) đi qua điểm 1 2 3( ; ; )M v| vuông góc với (d)? 
A. 2 4 0( ) :P x y z B. 2 3 7 0( ) :P x y z 
C. 2 3 4 0( ) :P x y z D. 2 7 0( ) :P x y z 
Câu 95: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): 2 2 22 3 1 25( ) ( ) ( )x y z 
v| mặt phẳng 3 4 12 7 0( ) : x y z . Xét vị trí tương đối của ( ) v| mặt cầu (S)? 
A. ( ) cắt (S) B. ( ) v| (S) không có điểm chung 
C. ( ) tiếp xúc (S) D. Không kết luận được. 
Câu 96: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình: 
4 3 5 6 0x y z . Xét mặt phẳng (Q): 8 6 10 3 3 0x y z m , m l| tham số thực. Tìm c{c 
gi{ trị của m để mặt phẳng (P) song song với mặt phẳng (Q)? 
A. 1m B. 1m C. 3m D. 3m 
Câu 97: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có t}m 2 1 3( ; ; )I , bán kính 5R 
v| mặt phẳng (P): 2 2 2 0x y z cắt (S) theo giao tuyến l| một đường tròn (C). Tìm tọa 
độ t}m J v| b{n kính r của đường tròn (C). 
A. 
2 5 1
3
3 3 3
; ; ,J r B. 
10 11 17
3
3 3 3
; ; ,J r 
C. 
2 5 1
4
3 3 3
; ; ,J r D. 
10 11 17
4
3 3 3
; ; ,J r 
Câu 98: Trong không gian với hệ tọa độ Oxyz, cho bốn điểm 
2 6 3 1 0 6 0 2 1 1 4 0( ; ; ), ( ; ; ), ( ; ; ), ( ; ; )A B C D . Viết phương trình mặt phẳng ( ) chứa AB v| 
song song với CD. 
A. 5 0( ) :x y B. 5 0( ) : x z 
C. 4 0( ) :y z D. 5 0( ) :x z 
Câu 99: Trong không gian với hệ tọa độ Oxyz, tính thể tích tứ diện OABC với A, B ,C lần lượt 
l| giao điểm của mặt phẳng 2x – 3y + 5z – 30 = 0 với trục Ox ,Oy ,Oz là: 
A. 78 B. 120 C. 91 D. 150 
 Câu 100: Trong không gian với hệ tọa độ Oxyz, cho điểm 1 0 7( ; ; )A và đường thẳng (d) có 
phương trình 
1 2
1 2 2
yx z
 . Viết phương trình đường thẳng ( ) đi qua A, vuông góc 
với (d) v| cắt (d). 
A. 
1 7
2 4 5
( ) :
yx z
 B. 
1 7
2 4 5
( ) :
yx z
C 
C. 
1 7
1 2 2
( ) :
yx z
 D. 
1 7
1 2 2
( ) :
yx z
Câu 101. Đồ thị hình bên l| của h|m số n|o? 
 A. 3 3 1y x x B. 3 23 1y x x 
 C. 3 3 1y x x D. 3 23 1y x x 
Câu 102. Cho h|m số ( )y f x có 
3
2 2
lim ( ) à lim ( )
x x
f x v f x . Khẳng định n|o sau đ}y 
đúng. 
A.Đồ thị h|m số đã cho không có tiệm cận ngang. 
B. Đồ thị h|m số đã cho có đúng một tiệm cận ngang. 
C. Đồ thị h|m số đã cho có hai tiệm cận đứng:
3
2 2
 à x v x . 
D. Đồ thị h|m số đã cho có hai tiệm cận đứng: 
3
2 2
 à yy v . 
Câu 103. Khoảng nghịch biến của h|m số 4 2
1
3 3
2
y x x là: 
 A. 3 0 3; ; B. 
3 3
0
2 2
; ; 
 C. 3(