3 Đề kiểm tra Chương I môn Giải tích Lớp 12 - Bùi Văn Thanh

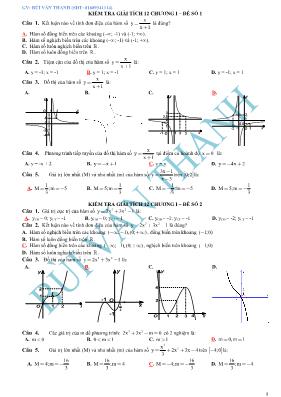
GV: BÙI VĂN THANH (SĐT: 01689341114) 
 1 
KIỂM TRA GIẢI TÍCH 12 CHƯƠNG I – ĐỀ SỐ 1 
Câu 1. Kết luận nào về tính đơn điệu của hàm số 
x
y
x 1


 là đúng? 
A. Hàm số đồng biến trên các khoảng (–; -1) và (-1; +). 
B. Hàm số nghịch biến trên các khoảng (–; -1) và (-1; +). 
C. Hàm số luôn nghịch biến trên  . 
D. Hàm số luôn đồng biến trên  . 
Câu 2. Tiệm cận của đồ thị của hàm số 
x
y
x 1


 là: 
A. y = -1; x = -1 B. y = 1; x = -1 C. y = 1; x = 1 D. y = -1; x = 1 
Câu 3. Đồ thị của hàm số 
x
y
x 1


 là: 
A. 
x
y
1
-4
-1
-2
-3
2O
B. 
C. 
x
y
1
2
2,5
3
3
2
-1 O 1
D. 
x
y
1
-1 O 1
2
-2
0.5
Câu 4. Phương trình tiếp tuyến của đồ thị hàm số 
x
y
x 1


 tại điểm có hoành độ x 0 là: 
A. y = -x + 2 B. y x 1  C. y = x D. y 4x 2  
Câu 5. Giá trị lớn nhất (M) và nhỏ nhất (m) của hàm số 
3x 1
y
x 3



trên  0;2 là: 
 A. 
1
M ;m 5
3
  B. 
1
M 5;m
3
  C. 
1
M ;m 5
3
  D. 
1
M 5;m
3
  
KIỂM TRA GIẢI TÍCH 12 CHƯƠNG I – ĐỀ SỐ 2 
Câu 1. Giá trị cực trị của hàm số 3 2y 2x 3x 1   là: 
A. yCĐ = 0; yCT = -1 B. yCĐ = 0; yCT = 1 C. yCĐ = -1; yCT = -1 D. yCĐ = -2; yCT = -1 
Câu 2. Kết luận nào về tính đơn điệu của hàm số 3 2y 2x 3x 1   là đúng? 
A. Hàm số nghịch biến trên các khoảng ( ; 1),(0; )  , đồng biến trên khoảng ( 1;0) 
B. Hàm số luôn đồng biến trên  . 
C. Hàm số đồng biến trên các khoảng ( ; 1),(0; )  , nghịch biến trên khoảng ( 1;0) 
D. Hàm số luôn nghịch biến trên  . 
Câu 3. Đồ thị của hàm số 3 2y 2x 3x 1   là: 
A. 
x
y
2
2
1
I
O 1
B. 
x
y
1
2
-1
O-1
C. 
x
y
2
3 4
4
2O 1
D. 
Câu 4. Các giá trị của m để phương trình: 3 22x 3x m 0   có 2 nghiệm là: 
A. m 0 B. 0 m 1  C. m 1 D. m 0,m 1  
Câu 5. Giá trị lớn nhất (M) và nhỏ nhất (m) của hàm số 
3
2xy 2x 3x 4
3
    trên  4;0 là: 
 A. 
16
M 4;m
3
  B. 
16
M ;m 4
3
  C. 
16
M 4;m
3
  D. 
16
M ;m 4
3
  
GV: BÙI VĂN THANH (SĐT: 01689341114) 
 2 
KIỂM TRA GIẢI TÍCH 12 CHƯƠNG I – ĐỀ SỐ 3 
Câu 1. Kết luận nào về tính đơn điệu của hàm số 
2x 1
y
x 1



 là đúng? 
A. Hàm số đồng biến trên các khoảng (–; 1) và (1; +). 
B. Hàm số nghịch biến trên các khoảng (–; 1) và (1; +). 
C. Hàm số luôn nghịch biến trên  . 
D. Hàm số luôn đồng biến trên  . 
Câu 2. Tiệm cận của đồ thị của hàm số 
2x 1
y
x 1



 là: 
A. y = 2; x = -1 B. y = -2; x = 1 C. y = -2; x = -1 D. y = 2; x = 1 
Câu 3. Đồ thị của hàm số 
2x 1
y
x 1



 là: 
A. 
x
y
1
-4
-1
-2
-3
2O
B. 
C. 
x
y
1
2
2,5
3
3
2
-1 O 1
D. 
x
y
1
-1 O 1
2
-2
0.5
Câu 4. Phương trình tiếp tuyến của đồ thị hàm số 
2x 1
y
x 1



 tại điểm có hoành độ 
1
x
2
 là: 
A. y = -x + 2 B. y x 1  C. y = x D. y 4x 2  
Câu 5. Giá trị lớn nhất (M) và nhỏ nhất (m) của hàm số 
x 1
y
x 4



trên  1;10 là: 
 A. 
11 2
M ;m
4 5
  B. 
2 11
M ;m
5 4
  C. 
11 2
M ;m
4 5
  D. 
2 11
M ;m
5 4
  
KIỂM TRA GIẢI TÍCH 12 CHƯƠNG I – ĐỀ SỐ 4 
Câu 1. Giá trị cực trị của hàm số 4 2y x 4x 3   là: 
A. yCT = 1 B. yCĐ = 3; yCT = -1 C. yCĐ = -3 D. yCĐ = 1; yCT = -3 
Câu 2. Kết luận nào về tính đơn điệu của hàm số 4 2y x 4x 3   là đúng? 
A. Hàm số đồng biến trên khoảng (0; ) , nghịch biến trên khoảng ( ;0) 
B. Hàm số nghịch biến trên khoảng ( 1; )  , đồng biến trên khoảng ( ; 1) . 
C. Hàm số đồng biến trên các khoảng ( ; 2),(0; 2) , nghịch biến trên các khoảng ( 2;0),( 2; )  
D. Hàm số nghịch biến trên các khoảng ( ; 2),(0; 2) , đồng biến trên các khoảng ( 2;0),( 2; )  
Câu 3. Đồ thị của hàm số 4 2y x 4x 3   là: 
A. 
B. 
C. 
D. 
Câu 4. Các giá trị của m để phương trình: 4 2x 4x m  có 4 nghiệm là: 
A. 1 m 3   B. 4 m 0   C. 1 m 3   D. 4 m 0   
Câu 5. Giá trị lớn nhất (M) và nhỏ nhất (m) của hàm số 4 2y 2x 4x 3   trên  0;2 là: 
 A. M 5;m 13  B. M 13;m 5  C. M 13;m 5  D. M 5;m 13 