Đại số và giải tích – Hình học 11 (các công thức cơ bản)

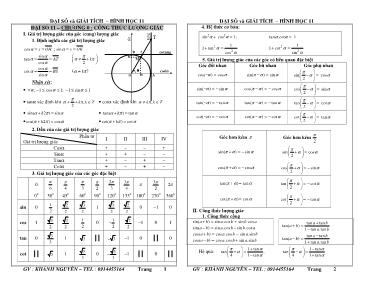
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 1 
ĐẠI SỐ 11 – CHƯƠNG 0 : CÔNG THỨC LƯỢNG GIÁC 
I. Giá trị lượng giác của góc (cung) lượng giác 
 1. Định nghĩa các giá trị lượng giác 
( )
cos ; sin
sintan
cos 2
coscot
sin
x OH y OK
AT k
BS k
α α
α pi
α α pi
α
α
α α pi
α
= = = =
 
= = ≠ + 
 
= = ≠
 Nhận xét: 
• , 1 cos 1; 1 sin 1α α α∀ − ≤ ≤ − ≤ ≤ 
• tanα xác định khi ,
2
k k Z
pi
α pi≠ + ∈ • cotα xác định khi ,k k Zα pi≠ ∈ 
• sin( 2 ) sinkα pi α+ = • tan( ) tankα pi α+ = 
• cos( 2 ) coskα pi α+ = • cot( ) cotkα pi α+ = 
 2. Dấu của các giá trị lượng giác 
Phần tư 
Giá trị lượng giác I II III IV 
Cosα + – – + 
Sinα + + – – 
Tanα + – + – 
Cotα + – + – 
 3. Giá trị lượng giác của các góc đặc biệt 
0 
6
pi
4
pi
3
pi
2
pi
2
3
pi
3
4
pi
pi 
3
2
pi
2pi 
00 300 450 600 900 1200 1350 1800 2700 3600 
sin 0 1
2
2
2
3
2
1 3
2
2
2
0 –1 0 
cos 1 3
2
2
2
1
2
0 1
2
− 
2
2
− 
–1 0 1 
tan 0 3
3
1 3 3− –1 0 0 
cot 3 1 3
3
0 3
3
− 
–1 0 
cosin 
O 
cotang 
s
i
n
t
a
n
g
H A 
M 
K 
B S 
α 
T 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 2 
 4. Hệ thức cơ bản: 
2 2sin cos 1α α+ = ; tan .cot 1α α = 
2
2
11 tan
cos
α
α
+ = 2
2
11 cot
sin
α
α
+ = 
 5. Giá trị lượng giác của các góc có liên quan đặc biệt 
Góc đối nhau Góc bù nhau Góc phụ nhau 
cos( ) cosα α− = sin( ) sinpi α α− = sin cos
2
pi
α α
 
− = 
 
sin( ) sinα α− = − cos( ) cospi α α− = − cos sin
2
pi
α α
 
− = 
 
tan( ) tanα α− = − tan( ) tanpi α α− = − tan cot
2
pi
α α
 
− = 
 
cot( ) cotα α− = − cot( ) cotpi α α− = − cot tan
2
pi
α α
 
− = 
 
Góc hơn kém pi Góc hơn kém 
2
pi
sin( ) sinpi α α+ = − sin cos
2
pi
α α
 
+ = 
 
cos( ) cospi α α+ = − cos sin
2
pi
α α
 
+ = − 
 
tan( ) tanpi α α+ = tan cot
2
pi
α α
 
+ = − 
 
cot( ) cotpi α α+ = cot tan
2
pi
α α
 
+ = − 
 
II. Công thức lượng giác 
 1. Công thức cộng 
sin( ) sin .cos sin .cosa b a b b a+ = + 
sin( ) sin .cos sin .cosa b a b b a− = − 
cos( ) cos .cos sin .sina b a b a b+ = − 
cos( ) cos .cos sin .sina b a b a b− = + 
 tan tantan( )
1 tan .tan
a b
a b
a b
+
+ =
−
tan tantan( )
1 tan .tan
a b
a b
a b
−
− =
+
Hệ quả: 1 tan 1 tantan , tan
4 1 tan 4 1 tan
pi α pi α
α α
α α
   + −
+ = − =   
− +   
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 3 
2. Công thức nhân đôi 
• sin2 2sin .cosα α α= • 2 2 2 2cos2 cos sin 2cos 1 1 2sinα α α α α= − = − = − 
•
2
2 tantan2
1 tan
α
α
α
=
−
 •
2cot 1cot 2
2cot
α
α
α
−
= 
Công thức hạ bậc Công thức nhân ba (*) 
2
2
2
1 cos2sin
2
1 cos2cos
2
1 cos2tan
1 cos2
α
α
α
α
α
α
α
−
=
+
=
−
=
+
3
3
3
2
sin3 3sin 4sin
cos3 4cos 3cos
3tan tantan3
1 3tan
α α α
α α α
α α
α
α
= −
= −
−
=
−
2. Công thức biểu diễn sina, cosa, tana theo t = tan
2
α
: 
2
2sin
1
t
t
α =
+
2
2
1cos
1
t
t
α
−
=
+
2
2tan
1
t
t
α =
−
 3. Công thức biến đổi tổng thành tích 
 cos cos 2cos .cos
2 2
a b a b
a b
+ −
+ = 
 cos cos 2sin .sin
2 2
a b a b
a b
+ −
− = −
sin sin 2sin .cos
2 2
a b a b
a b
+ −
+ =
sin sin 2cos .sin
2 2
a b a b
a b
+ −
− = 
sin( )tan tan
cos .cos
a b
a b
a b
+
+ = 
sin( )
tan tan
cos .cos
a b
a b
a b
−
− = 
sin( )cot cot
sin .sin
a b
a b
a b
+
+ = 
sin( )
cot cot
sin .sin
b a
a b
a b
−
− = 
sin cos 2.sin 2.cos
4 4
pi pi
α α α α
   
+ = + = −   
   
sin cos 2 sin 2 cos
4 4
pi pi
α α α α
   
− = − = − +   
   
 4. Công thức biến đổi tích thành tổng 
 1co s . c o s co s ( ) co s ( )
2
1s in . s in c o s ( ) co s ( )
2
1s in . co s s in ( ) s in ( )
2
a b a b a b
a b a b a b
a b a b a b
 = − + + 
 = − − + 
 = − + + 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 4 
ĐẠI SỐ 11 – CHƯƠNG 1 : HÀM SỐ LƯỢNG GIÁC – 
PHƯƠNG TRÌNH LƯỢNG GIÁC 
I –HÀM SỐ LƯỢNG GIÁC 
TẬP XÁC ĐỊNH, TẬP GIÁ TRỊ, TÍNH CHẴN – LẺ, CHU KỲ 
HÀM SIN HÀM COSIN 
siny x= 
*Tập xác định D = R; 
*Tập giá trị 1, 1T  = −  ; hàm lẻ 
*Chu kỳ 0 2T pi= 
*y = sin(ax + b) có CK : 0
2
T
a
pi
= 
* y = sin(f(x)) xác định 
( )f x⇔ xác định. 
cosy x= 
*TXĐ : D = R 
*Tập giá trị 1, 1T  = −  ; hàm chẵn, 
* Chu kỳ 0 2T pi= . 
* y = cos(ax + b) có CK : 0
2
T
a
pi
= 
* y = cos(f(x)) xác định 
 ( )f x⇔ xác định. 
HÀM TANG HÀM COTANG 
tany x= 
*TXĐ \ ,
2
D R k k Z
pi
pi
 
= + ∈ 
 
*Tập giá trị T = R, hàm lẻ, 
* Chu kỳ 0T pi= . 
*y = tan(ax + b) có chu kỳ 0T a
pi
= 
*y = tan(f(x)) xác định 
( )f x⇔ ( )
2
k k Z
pi
pi≠ + ∈ 
coty x= 
*TXĐ { }\ ,D R k k Zpi= ∈ ; 
*Tập giá trị T = R, hàm lẻ 
*Chu kỳ 0T pi= . 
*y = cot(ax + b) có chu kỳ 0T a
pi
= 
*y = cot(f(x)) xác định 
( ) ( )f x k k Zpi⇔ ≠ ∈ 
* y = f1(x) có chu kỳ T1 ; y = f2(x) có chu kỳ T2 thì hàm số 
1 2( ) ( )y f x f x= ± có chu kỳ T0 là bội chung NN của T1 và T2. 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 5 
ĐỒ THỊ CỦA HÀM SỐ LƯỢNG GIÁC 
1) Vẽ đồ thị hàm số lượng giác: 
– Tìm tập xác định D. – Tìm chu kỳ T0 của hàm số. 
– Xác định tính chẵn – lẻ (nếu cần). 
– Lập bảng biến thiên trên một đoạn có độ dài bằng chu kỳ T0 có thể 
chọn : 00,x T ∈   hoặc 
0 0,
2 2
T T
x
 
∈ − 
  
– Vẽ đồ thị trên đoạn có độ dài bằng chu kỳ. 
– Rồi suy ra phần đồ thị còn lại bằng phép tịnh tiến theo vectơ 0. .v k T i=



về bên trái và phải song song với trục hoành Ox (với i


 là véc tơ đơn 
vị trên trục Ox). 
2) Một số phép biến đổi đồ thị: 
a) Từ đồ thị hàm số y = f(x), suy ra đồ thị hàm số y = f(x) + a bằng cách 
tịnh tiến đồ thị y = f(x) lên trên trục hoành a đơn vị nếu a > 0 và tịnh 
tiến xuống phía dưới trục hoành a đơn vị nếu a < 0. 
b) Từ đồ thị y = f(x), suy ra đồ thị y = –f(x) bằng cách lấy đối xứng đồ thị 
y = f(x) qua trục hoành. 
c) Đồ thị ( ), ( ) 0( )
( ), ( ) 0
f x neáu f x
y f x
f x neáu f x
 ≥
= = 
− <
 được suy từ đồ thị y = f(x) 
bằng cách giữ nguyên phần đồ thị y = f(x) ở phía trên Ox và lấy đối 
xứng phần đồ thị y = f(x) nằm ở phía dưới trục hoành qua Ox. 
Ví dụ 1: Vẽ đồ thị hàm số y = f(x) = sinx. 
– Tập xác định: D = R. – Tập giá trị: 1, 1 . −  
– Chu kỳ: T = 2pi . –Bảng biến thiên trên đoạn 0, 2pi   
x 0 
2
pi
pi 
3
2
pi
2pi 
y 
1 
0 
–1 
0 0 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 6 
– Tịnh tiến theo véctơ 2 .v k ipi=

 

 ta được đồ thị y = sinx. 
Nhận xét: 
– Đồ thị là một hàm số lẻ nên nhận gốc tọa độ O làm tâm đối xứng. 
– Hàm số ĐB trên khoảng 0,
2
pi 
 
 
 và nghịch biến trên , .
2
pi
pi
 
 
 
Ví dụ 2: Vẽ đồ thị hàm số y = f(x) = cosx. 
– Tập xác định: D = R. – Tập giá trị: 1, 1 . −  
– Chu kỳ: T = 2pi . – Bảng biến thiên trên 0, 2 :pi   
– Tịnh tiến theo véctơ 2 .v k ipi=

 

 ta được đồ thị y = cosx. 
Nhận xét: 
– Đồ thị là một hàm số chẵn nên nhận Oy làm trục đối xứng. 
– Hàm số ĐB trên khoảng 0,
2
pi 
 
 
 và NB trên khoảng 3, .
2
pi
pi
 
 
 
x 0 
2
pi
pi 
3
2
pi
2pi 
y 
0 
–1 
0 
1 1 
1 
3
2
pi
−
−pi
2
pi
−
0 
2
pi 3
2
pi pi 2pi 5
2
pi
y = cosx 
–1 
y 
x 
1 
3
2
pi
−
−pi
2
pi
−
0 
2
pi 3
2
pi pi 2pi 5
2
pi
y = sinx 
–1 
y 
x 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 7 
Ví dụ 3: Vẽ đồ thị hàm số y = f(x) = tanx. 
– Tập xác định: D = R \ ,
2
k k Z
pi
pi
 
+ ∈ 
 
 – Tập giá trị: R. 
– Giới hạn: 
/2
lim
x
y
pi→±
= ∞ :
2
x
pi
⇒ = ± là tiệm cận đứng. 
– Chu kỳ: T = pi . – Bảng biến thiên trên ,
2 2
pi pi 
− 
 
 : 
– Tịnh tiến theo véctơ .v k ipi=

 

 ta được đồ thị y = tanx. 
Nhận xét: 
– Đồ thị là một hàm số lẻ nên nhận gốc tọa độ O làm tâm đối xứng. 
– Hàm số luôn đồng biến trên tập xác định D. 
Ví dụ 4: Vẽ đồ thị hàm số y = f(x) = cotx. 
– Tập xác định: D = R { }\ ,k k Zpi ∈ – Tập giá trị: R. 
– Giới hạn: 
0
lim , lim
x x x
y y
→ →
= +∞ = −∞ ,tiệm cận đứng: x = 0, x =pi 
– Chu kỳ: T = pi . – BBT trên đoạn 0, pi   
x 
2
pi
− 0 
2
pi
y 
0 
–∞ 
+∞ 
x 0 / 2pi pi 
y 
0 
+∞ 
–∞ 
x 
y 
3
2
pi
−
pi 
2
pi
−
O 
2
pi pi 3
2
pi 2pi 5
2
pi
y = tanx 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 8 
– Tịnh tiến theo véctơ .v k ipi=

 

 ta được đồ thị y = cotx. 
Nhận xét: 
– Đồ thị là một hàm số lẻ nên nhận gốc tọa độ O làm tâm đối xứng. 
– Hàm số luôn giảm trên tập xác định D. 
Ví dụ 5: Vẽ đồ thị y = – sinx. 
–Vẽ đồ thị y = sinx. 
– Từ đồ thị y = sinx, ta suy ra đồ thị y = –sinx bằng cách lấy đ/xứng qua Ox. 
Ví dụ 6: Vẽ đồ thị sin , neu sin x 0sin
-sin x, neu sin x < 0.
x
y x
 ≥
= = 

Ví dụ 7: Vẽ đồ thị hàm số y = 1 + cosx. 
– Vẽ đồ thị y = cosx. 
– Từ đồ thị y = cosx, ta suy ra đồ thị 1 cosy x= + bằng cách tịnh tiến đồ 
thị cosy x= lên trục hoành 1 đơn vị. 
x 
y 
2− pi 3
2
pi
−
O 
2
pi
− 
2
pi pi 3
2
pi 
y = cotx 
−pi 2pi 
y 
x –2 3
2
pi
−
3
2
pi
2pi 
2
pi
pi O −pi 
2
pi
− 
y = –sinx 1 
–1 
pi 
2
pi
−
3
2
pi
2pi 
2
pi
pi O 
y = /sinx/ 
y 
1 
x 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 9 
– Bảng biến thiên trên đoạn 0, 2pi   : 
Ví dụ 8: Vẽ đồ thị y = sin2x. 
– y = sin2x có chu kỳ T = pi - BBT trên đoạn 0, 2pi   : 
x 0 
2
pi
pi 
3
2
pi
2pi 
y = cosx 
1 
0 
–1 
0 
1 
y = 1 + cosx 
2 
1 
0 
1 
2 
2
pi
− O 
y = 1 + cosx 
y 
x −pi 
2
pi pi 3
2
pi 
y = cosx 
2 
1 
–1 
x 
2
−
pi
4
−
pi
0 
2
pi
2
pi
2x −pi 
2
pi
− 0 
2
pi
pi 
y = sin2x 
0 
–1 
0 
1 
0 
2
pi
−
O 
y 
x pi 
4
pi
− 
4
pi 
1 
3
2
pi 
2
pi 5
4
pi 
y = sin2x 
–1 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 10 
Ví dụ 9: Vẽ đồ thị y = cos2x. 
– y = cos2x có chu kỳ T = pi 
– Bảng biến thiên trên đoạn 0, 2pi   : 
II. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN 
1. Phương trình sinx = sinα 
•
2
sin sin ( )
2
x k
x k Z
x k
α pi
α
pi α pi
 = +
= ⇔ ∈
= − +
• 
arcsin 2
sin ( ) ( 1 1)
arcsin 2
x a k
x a k Z a
x a k
pi
pi pi
 = +
= ⇔ ∈ − ≤ ≤
= − +
Các trường hợp đặc biệt 
• sin sin sin sin( )u v u v= − ⇔ = − 
• sin 1 2
2
x x k
pi
pi= − ⇔ = − + 
• sin cos sin sin
2
u v u v
pi 
= ⇔ = − 
 
• sin 0 ( )x x k k Zpi= ⇔ = ∈ 
• sin cos sin sin
2
u v u v
pi 
= − ⇔ = − 
 
 • sin 1 2 ( )
2
x x k k Z
pi
pi= ⇔ = + ∈ 
• 
2 2sin 1 sin 1 cos 0 cos 0 ( )
2
x x x x x k k Z
pi
pi= ± ⇔ = ⇔ = ⇔ = ⇔ = + ∈ 
O 
y 
x 
2
pi
4
pi
1 
2
pi
4
pi
y = cos2x 
–1 
3
4
pi
x 
2
pi
− 
4
pi
− 0 
4
pi
2
pi
2x −pi 
2
pi
− 0 
2
pi
pi 
y = cos2x 
–1 
0 
1 
0 
–1 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 11 
2. Phương trình cosx = cosα 
• cos cos 2 ( )x x k k Zα α pi= ⇔ = ± + ∈ 
• cos arccos 2 ( )( 1 1)x a x a k k Z api= ⇔ = ± + ∈ − ≤ ≤ 
Các trường hợp đặc biệt 
• cos cos cos cos( )u v u vpi= − ⇔ = − • cos 1 2 ( )x x k k Zpi= ⇔ = ∈ 
• cos sin cos cos
2
u v u v
pi 
= ⇔ = − 
 
 • cos 0 ( )
2
x x k k Z
pi
pi= ⇔ = + ∈ 
• cos sin cos cos
2
u v u v
pi 
= − ⇔ = + 
 
• cos 1 2 ( )x x k k Zpi pi= − ⇔ = + ∈ 
•
2 2cos 1 cos 1 sin 0 sin 0 ( )x x x x x k k Zpi= ± ⇔ = ⇔ = ⇔ = ⇔ = ∈ 
3. Phương trình tan x = tanα 
• tan tanx x kα α pi= ⇔ = + • tan arctanx a x a kpi= ⇔ = + 
Các trường hợp đặc biệt 
• tan tan tan tan( )u v u v= − ⇔ = − • tan 0 ( )x x k k Zpi= ⇔ = ∈ 
• tan cot tan tan
2
u v u v
pi 
= ⇔ = − 
 
 • tan 1 ( )
4
x x k k Z
pi
pi= ± ⇔ = ± + ∈ 
• tan cot tan tan
2
u v u v
pi 
= − ⇔ = + 
 
 • tan 3 ( )
3
x x k k Z
pi
pi= ± ⇔ = ± + ∈ 
4. Phương trình cotx = cotα 
• cot cotx x kα α pi= ⇔ = + • cot arccotx a x a kpi= ⇔ = + 
Các trường hợp đặc biệt 
• cot cot cot cot( )u v u v= − ⇔ = − 
• cot 0 ( )
2
x x k k Z
pi
pi= ⇔ = + ∈ 
• cot 1 ( )
4
x x k k Z
pi
pi= ± ⇔ = ± + ∈ • cot 3 ( )
6
x x k k Z
pi
pi= ± ⇔ = ± + ∈ 
5. Một số điều cần chú ý: 
a) Khi giải phương trình có chứa các hàm số tang, cotang, có mẫu số 
hoặc chứa căn bậc chẵn, thì nhất thiết phải đặt điều kiện để 
phương trình xác định. 
* Phương trình chứa tanx thì điều kiện: ( ).
2
x k k Z
pi
pi≠ + ∈ 
* Phương trình chứa cotx thì điều kiện: ( )x k k Zpi≠ ∈ 
* PT chứa cả tanx và cotx thì điều kiện ( )
2
x k k Z
pi
≠ ∈ 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 12 
* Phương trình có mẫu số: 
• sin 0 ( )x x k k Zpi≠ ⇔ ≠ ∈ 
• cos 0 ( )
2
x x k k Z
pi
pi≠ ⇔ ≠ + ∈ 
• tan 0 ( )
2
x x k k Z
pi
≠ ⇔ ≠ ∈ • cot 0 ( )
2
x x k k Z
pi
≠ ⇔ ≠ ∈ 
b) Khi tìm được nghiệm phải kiểm tra điều kiện. Ta thường dùng 
một trong các cách sau để kiểm tra điều kiện: 
1.Kiểm tra trực tiếp bằng cách thay giá trị của x vào điều kiện. 
2.Dùng đường tròn lượng giác. 
3.Giải các phương trình vô định. 
II. PT BẬC HAI ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC 
Dạng Đặt Điều kiện 
2 sin 0asin x b x c+ + = t = sinx 1 1t− ≤ ≤ 
2cos cos 0a x b x c+ + = t = cosx 1 1t− ≤ ≤ 
2tan tan 0a x b x c+ + = t = tanx ( )
2
x k k Z
pi
pi≠ + ∈ 
2cot cot 0a x b x c+ + = t = cotx ( )x k k Zpi≠ ∈ 
Nếu đặt: 2sin sin 0 1.t x hay t x thì t= = ≤ ≤ 
III. PHƯƠNG TRÌNH BẬC NHẤT THEO SINX VÀ COSX 
DẠNG: a sinx + b cosx = c (1) 
• Điều kiện để PT có nghiệm là : 2 2 2 .a b c+ ≥ 
Cách 1: 
(1) ⇔ 
2 2 2 2 2 2
sin cosa b cx x
a b a b a b
+ =
+ + +
⇔
2 2
cos( ) cos− = =
+
c
x
a b
α β 2 ( )x k k Zα β pi⇔ = ± + ∈ 
(với ( )
2 2 2 2
sin , cos 0, 2a b
a b a b
α α α pi = = ∈  
+ +
 ) 
Cách 2: a) Xét 2
2 2
x
x k k
pi
pi pi pi= + ⇔ = + có là nghiệm hay không? 
b) Xét 2 cos 0.
2
x
x kpi pi≠ + ⇔ ≠ 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 13 
Đặt: 
2
2 2
2 1tan , sin , cos ,
2 1 1
x t t
t thay x x
t t
−
= = =
+ +
 ta được PT bậc hai theo t: 2( ) 2 0 (3)b c t at c b+ − + − = 
 Giải (3), với mỗi nghiệm t0, ta có phương trình: 0tan .2
x
t= 
DẠNG: a sin2x + b sinx.cosx + c cos2x = d (1) 
Cách 1: 
• Kiểm tra cosx = 0 có thoả mãn (1) hay không? 
 Lưu ý: cosx = 0 2sin 1 sin 1.
2
x k x x
pi
pi⇔ = + ⇔ = ⇔ =± 
• Khi cos 0x ≠ , chia hai vế phương trình (1) cho 2cos 0x ≠ ta được: 
2 2. tan .tan (1 tan )a x b x c d x+ + = + 
Cách 2: Dùng công thức hạ bậc 
1 cos2 sin2 1 cos2(1) . . .
2 2 2
x x x
a b c d
− +
⇔ + + = 
 .sin2 ( ).cos2 2b x c a x d a c⇔ + − = − − 
(đây là PT bậc nhất đối với sin2x và cos2x) 
V. PHƯƠNG TRÌNH ĐỐI XỨNG 
Dạng 1: a.(sinx ± cosx) + b.sinx.cosx + c = 0 
• Đặt: cos sin 2.cos ; 2.
4
t x x x t
pi 
= ± = ≤ 
 
∓ 
2 211 2sin .cos sin .cos ( 1).
2
t x x x x t⇒ = ± ⇒ = ± − 
• Thay vào PT đã cho, ta được PT bậc hai theo t. Giải PT này tìm t thỏa 
2.t ≤ Suy ra x. 
Dạng 2: a.|sinx ± cosx| + b.sinx.cosx + c = 0 
• Đặt: cos sin 2. cos ; : 0 2.
4
t x x x Ñk t
pi 
= ± = ≤ ≤ 
 
∓ 
21sin .cos ( 1).
2
x x t⇒ = ± − 
• Tương tự dạng trên. Khi tìm x cần lưu ý PT chứa dấu giá trị tuyệt đối. 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 14 
ĐẠI SỐ 11 – CHƯƠNG 2 : TỔ HỢP – XÁC SUẤT 
I. Qui tắc đếm 
1. Qui tắc cộng: 
 Một công việc nào đó có thể được thực hiện theo một trong hai 
phương án A hoặc B. Nếu phương án A có m cách thực hiện, phương 
án B có n cách thực hiện và không trùng với bất kì cách nào trong 
phương án A thì công việc đó có m + n cách thực hiện. 
2. Qui tắc nhân: 
 Một công việc nào đó có thể bao gồm hai công đoạn A và B. Nếu 
công đoạn A có m cách thực hiện và ứng với mỗi cách đó có n cách 
thực hiện công đoạn B thì công việc đó có m.n cách thực hiện. 
II. Hoán vị 
1. Giai thừa: 
•n! = 1.2.3n •Qui ước: 0! = 1 • n! = (n–1)!n 
•
!
!
n
p
= (p+1).(p+2)n . (với n>p) • !
( )!
n
n p−
= (n–p+1).(n–p+2)n 
(với n>p) 
2. Hoán vị (không lặp): Một tập hợp gồm n phần tử (n ≥ 1). Mỗi cách sắp 
xếp n phần tử này theo một thứ tự nào đó được gọi là một hoán vị của n 
phần tử. Số các hoán vị của n phần tử là: Pn = n! 
3. Hoán vị lặp : Cho k phần tử khác nhau: a1, a2, , ak. Một cách sắp xếp 
n phần tử trong đó gồm n1 phần tử a1, n2 phần tử a2, , nk phần tử ak 
(n1+n2+ + nk = n) theo một thứ tự nào đó được gọi là một hoán vị lặp cấp 
n và kiểu (n1, n2, , nk) của k phần tử. Số các hoán vị lặp cấp n, kiểu (n1, 
n2, , nk) của k phần tử là: Pn(n1, n2, , nk) = 
1 2
!
! !... !k
n
n n n
4. Hoán vị vòng quanh : Cho tập A gồm n phần tử. Một cách sắp xếp n 
phần tử của tập A thành một dãy kín được gọi là một hoán vị vòng 
quanh của n phần tử. Số các hoán vị vòng quanh của n phần tử là: 
Qn = (n – 1)! 
III. Chỉnh hợp 
1. Chỉnh hợp (không lặp): Cho tập hợp A gồm n phần tử. Mỗi cách sắp 
xếp k phần tử của A (1 ≤ k ≤ n) theo một thứ tự nào đó được gọi là 
một chỉnh hợp chập k của n phần tử của tập A.Số chỉnh hợp chập k 
của n phần tử: !( 1)( 2)...( 1)
( )!
k
n
n
A n n n n k
n k
= − − − + =
−
 • Công thức trên cũng đúng cho trường hợp k = 0 hoặc k = n. 
 • Khi k = n thì nnA = Pn = n! 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 15 
2. Chỉnh hợp lặp: 
 Cho tập A gồm n phần tử. Một dãy gồm k phần tử của A, trong đó mỗi 
phần tử có thể được lặp lại nhiều lần, được sắp xếp theo một thứ tự 
nhất định được gọi là một chỉnh hợp lặp chập k của n phần tử của tập 
A. Số chỉnh hợp lặp chập k của n phần tử: k knA n= 
IV. Tổ hợp 
1. Tổ hợp (không lặp) : Cho tập A gồm n phần tử. Mỗi tập con gồm k (1 
≤ k ≤ n) phần tử của A được gọi là một tổ hợp chập k của n phần tử. 
 Số các tổ hợp chập k của n phần tử: !
! !( )!
k
k n
n
A n
C
k k n k
= =
−
 • Qui ước: 0 nn nC C= = 1 
 Tính chất: 
0 1;n k n kn n n nC C C C
−
= = = 
1
1 1
k k k
n n nC C C
−
− −
= + 11k k
n n
n k
C C
k
−
− +
= 
2. Tổ hợp lặp: Cho tập A = { }1 2; ;...; na a a và số tự nhiên k bất kì. Một tổ 
hợp lặp chập k của n phần tử là một hợp gồm k phần tử, trong đó mỗi phần 
tử là một trong n phần tử của A. Số tổ hợp lặp chập k của n phần tử: 
1
1 1
k k m
n n k n kC C C
−
+ − + −= = 
3. Phân biệt chỉnh hợp và tổ hợp: 
 • Chỉnh hợp và tổ hợp liên hệ nhau bởi công thức: !k kn nA k C= 
 • Chỉnh hợp: có thứ tự. Tổ hợp: không có thứ tự. 
⇒ Những bài toán mà kết quả phụ thuộc vào vị trí các phần tử –> chỉnh 
hợp . Ngược lại, là tổ hợp. 
 • Cách lấy k phần tử từ tập n phần tử (k ≤ n): 
 + Không thứ tự, không hoàn lại: knC 
+ Có thứ tự, không hoàn lại: knA + Có thứ tự, có hoàn lại: 
k
nA 
V. Nhị thức Newton 
1. Công thức khai triển nhị thức Newton: 
Với mọi n∈N và với mọi cặp số a, b ta có: 
0
( )
n
n k n k k
n
k
a b C a b−
=
+ = ∑ 
2. Tính chất: 
 1) Số các số hạng của khai triển bằng n + 1 
 2) Tổng các số mũ của a và b trong mỗi số hạng bằng n 
 3) Số hạng tổng quát (thứ k+1) có dạng: 
Tk+1 = k n k knC a b
−
 ( k =0, 1, 2, , n) 
ĐẠI SỐ và GIẢI TÍCH – HÌNH HỌC 11 
GV : KHÁNH NGUYÊN – TEL : 0914455164 Trang 16 
 4) Các hệ số của các cặp số hạng cách đều số hạng đầu và cuối thì 
bằng nhau: k n kn nC C
−
= 
 5) 0 1nn nC C= = , 1 1k k kn n nC C C− ++ = 
Nhận xét : Nếu trong khai triển nhị thức Newton, ta gán cho a và b những 
giá trị đặc biệt thì ta sẽ thu được những công thức đặc biệt. Chẳng hạn: 
(1+x)n = 0 1 1 ...n n nn n nC x C x C−+ + + ⇒ 0 1 ... 2n nn n nC C C+ + + = 
(x–1)n = 0 1 1 ... ( 1)n n n nn n nC x C x C−− + + − ⇒ 0 1 ... ( 1) 0n nn n nC C C− + + − = 
VI. Biến cố và xác suất 
1. Biến cố 
• Không gian mẫu Ω: là tập các kết quả có thể xảy ra của một phép thử. 
• Biến cố A: là tập các kết quả của phép thử làm xảy ra A. A ⊂ Ω. 
• Biến cố không: ∅ • Biến cố chắc chắn: Ω 
• Biến cố đối của A: \A A= Ω • Hợp hai biến cố: A ∪ B