Bài tập Thể tích khối đa diện

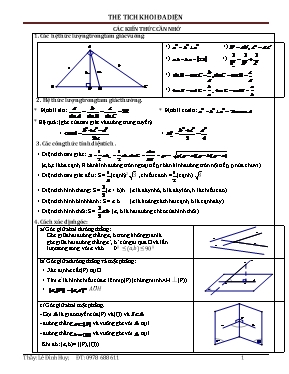
 CÁC KIẾN THỨC CẦN NHỚ 
1. Các hệ thức lượng trong tam giác vuông:
+) +) 
+) +) 
+) 
+) 
 2. Hệ thức lượng trong tam giác thường.
* Định lí sin: * Định lí cosin: 
* Hệ quả: (góc của tam giác và đường trung tuyến)
 + + 
 3. Các công thức tính diện tích . 
 + Diện tích tam giác: 
 (a,b,c là ba cạnh, R bán kính đường tròn ngoại tiếp, r bán kính đường tròn nội tiếp, p nửa chu vi)
 + Diện tích tam giác đều: S =(cạnh)2.3 , chiều cao h =(cạnh). 3
 + Diện tích hình thang: S =(a + b)h (a là đáy nhỏ, b là đáy lớn, h là chiều cao)
 + Diện tích hình bình hành: S = a.b (a là koảng cách hai cạnh, b là cạnh đáy)
 + Diện tích hình thôi: S = (a, b là hai đường chéo của hình thôi)
4. Cách xác định góc:
a/ Góc giữa hai đường thẳng:
 Góc giữa hai đường thẳng a, b trong không gian là 
 góc giữa hai đường thẳng a’, b’ cùng đi qua O và lần 
 lượt song song với a và b. 00 ≤(a,b)≤900 
b/ Góc giữa đường thẳng và mặt phẳng:
 + Xác định a cắt (P) tại O
 + Tìm a’ là hình chiếu của a lên mp(P) (chứng minh AH ⏊ (P))
 + = AOH 
c/ Góc giữa hai mặt phẳng. 
- Gọi là giao tuyến của (P) và (Q) và 
- đường thẳng và vuông góc với tại I
- đường thẳng và vuông góc với tại I
 Khi đó: (a,b) = ((P),(Q))
5. Các cách xác định khoảng cách: d
 a/ Khoảng cách từ điểm M đến mặt phẳng (P) M
 Cách 1: Nếu đường thẳng d vuông góc (P), ta tìm hình chiếu H
 của M lên mp(P) song song với d, nên MH vuông góc (P). H
 Suy ra: MH = d(M,(P)) P
 Cách 2: Xác định mp(Q) qua điểm M 
 Chứng minh (P) vuông góc (Q) theo giao tuyến d 
 Kẽ MH vuông góc với d, nên MH vuông góc (P) M
 Suy ra: MH = d(M,(P))
 Q H P
 b/ Khoảng cách từ đường thẳng a đến mặt phẳng (P) song song. 
 Chọn điểm M thuộc a, tìm hình chiếu H của M lên mp(P). Suy ra: MH = d(M,(P)) = d(a,(P)).
 c/ Khoảng cách giữa hai mp song song. (tương tự b)
 d/ Khoảng cách giữa hai đường thẳng a và b chéo nhau.
 A b b
 a 
 H a A 
 P P H
 Cách 1: Xác định mp(P) chứa a và song song với đường thẳng b. Suy ra: d(a,b) = d(b,(P)) = AH
 Cách 2: Xác định mp(P) chứa a và chứng minh b cắt và vuông góc mp(P) tại A
 Từ A kẽ AH vuông góc a tại H, nên AH ⏊ a và AH ⏊ b. Suy ra: d(a,b) = AH 
 THỂ TÍCH KHỐI CHÓP VÀ KHỐI LĂNG TRỤ
1. Thể tích của một khối đa diện
 + Hai khối đa diện bằng nhau thì có thể tích bằng nhau.
 + Nếu một khối đa diện được phân chia thành nhiều khối đa diện nhỏ, thì thể tích của nó bằng 
 tổng thể tích của các khối đa diện nhỏ đó.
 + Khối lập phương có cạnh bằng 1 thì có thể tích bằng 1.
2. Thể tích của khối hộp chữ nhật: Thể tích của một khối hộp chữ nhật bằng tích số của 3 kích
 thước : V = a.b.c 
3. Thể tích của khối lăng trụ: Thể tích của khối lăng trụ bằng tích số của diện tích mặt đáy và 
 chiều cao : V = Sđáy.h
4. Thể tích của khối chóp: Thể tích của một khối chóp bằng một phần ba tích số của diện tích 
 mặt đáy và chiều cao : V = Sđáy.h
 PHƯƠNG PHÁP TÍNH THỂ TÍCH HÌNH CHÓP, HÌNH LĂNG TRỤ
 B1: Xác định chiều cao hình chóp (hình lăng trụ) hạ từ đỉnh vuông góc mp đáy S
 B2: Xác định các yêu cầu bài toán cho
 B3: Xác định công thức tính thể tích và tính thể tích đó A1 C1
Chú ý: + Nếu khối chóp không tính được thể tích V, ta có thể xác định V = kV1
 Ta tính thể tích V1 và suy ra V B1
 + Ta có thể áp dụng công thức tính tỉ số thể tích của khối chóp A C
 tam giác suy ra V = kV1 B
 PHẦN 1 – KHỐI CHÓP
1. Hình chóp đều: Là hình chóp có đáy là đa giác đều và có các cạnh bên bằng nhau.
• Đáy ABC là tam giác đều, SO = h là chiều cao.
• SAO là góc giữa SA với mặt đáy (ABCD)
• SEO là góc giữa mặt bên (SBC) với mặt đáy.
• Đáy ABCD là hình vuông, SO = h là chiều cao.
• SAO là góc giữa SA với mặt đáy (ABCD)
• SEO là góc giữa mặt bên (SCD) với mặt đáy.
1) Cho hình chóp đều SABC có cạnh bên bằng a hợp với đáy ABC một góc 60o . Tính thể tích hình chóp. 
2) Cho hình chóp tứ giác đều S.ABCD có cạnh bằng , và SH là đường cao của hình chóp. Khoảng cách 
 từ trung điểm I của SH đến mặt bên (SDC) bằng . Tìm thể VS.ABCD = ? 
3) (CĐ-09) Cho hình chóp đều S.ABCD có Gọi M, N và P lần lượt là trung điểm của 
 SA, SB, CD. Chứng minh . Tính thể tích của khối tư diện 
4) Cho hình chóp tam giác đều S.ABC có cạch AB = a, các cạnh bên SA, SB, SC tạo với đáy một góc 600. 
 Gọi D là giao điểm của SA với mp qua BC và vuông góc với SA.
 a, Tính tỉ số thể tích của hai khối chóp S.DBC và S.ABC. 
 b, Tính thể tích của khối chóp S.DBC 
5) Cho hình chóp tứ giác đều S.ABCD, có đáy là hình vuông tâm O cạnh bằng a, mặt bên tạo với mặt đáy 
 một góc 600.
 a, Tính thể tích của tứ giác S.ABCD và tính khoảng cách từ từ O đến mp(SCD).
 b, M là trung điểm của cạnh SB, mp() qua CD và trung điểm M của SB chia khối chóp thành hai phần.
 Tính tỉ số thể tích hai phần đó.
 ĐS:1, 2, 3, 4, , V = 5,, d = ,
2. Hình chóp có cạnh bên vuông góc với mặt đáy 
 (có hai mặt bên cùng vuông góc với đáy, có mặt bên vuông góc với đáy)
 S S S
 A D A D 
 A C H 
 H
 B C C
 B B
 - Cạnh bên vuông góc với đáy: Là chiều cao của khối chóp
 - Mặt bên vuông góc với đáy: Đường cao của khối chóp = đường cao của mặt đó và chân đường cao 
 thuộc giao tuyến
 - Hai mặt bên vuông góc với đáy: Đường cao là giao tuyến của hai mặt bên đó
1)(TN–13) Cho hình chóp có đáy là hình vuông cạnh , cạnh bên vuông góc với 
 mặt phẳng đáy. Đường thẳng tạo với mp một góc .Tính thể tích của khối chóp 
2)(KD-13) Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, SA vuông góc với đáy, BÂD = 1200, 
 M là trung điểm cạnh BC và SMA = 450. Tính theo a thể tích của khối chóp S.ABCD và d[D;(SBC)] .
3)(KA – 11) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a, hai mp(SAB)
 và (SAC) cùng vuông góc với mp(ABC). Gọi M là trung điểm của AB, mặt phẳng qua SM và song song 
 với BC, cắt AC tại N. Biết góc giữa 2mp(SBC) và (ABC) bằng 600. Tính thể tích khối chóp S.BCNM và 
 khoảng cách giữa hai đường thẳng AB và SN theo a. 
4)(KA-13) Cho hình chóp S.ABC có đáy là tam giác vuông tại A, ABC = 300, SBC là tam giác đều cạnh a 
 và mặt bên SBC vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC và tính d[C;(SAB)]
5)(KA -12) Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên
 mp(ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB. Góc giữa đường thẳng SC và mp(ABC) bằng
 600. Tính thể tích của khối chóp S.ABC và tính khoảng cách giữa hai đường thẳng SA và BC theo a. 
6)(KA – 10) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm 
 của các cạnh AB và AD, H là giao điểm của CN và DM. Biết SH vuông góc mp(ABCD) và SH = 
 Tính thể tích của khối chóp SCDNM và khoảng cách giữa hai đường thẳng DM và SC theo a.
 ĐS: 1. V = 2. V =, d = 3. V =, d = 4. V =, d = 
 5. 6. V = , d = 
⍟ Bài tập tương tự:
 1)(KB -12) Cho hình chóp tam giác đều S.ABC với SA = 2a, AB = a. Gọi H là hình chiếu vuông góc của A 
 trên cạnh SC. Chứng minh SC vuông góc với mp(ABH). Tính thể tích của khối chóp S.ABH theo a. 
 2)(KD – 10) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = a, hình chiếu 
 vuông góc của đỉnh S trên mp(ABCD) là điểm H thuộc đoạn AC, AH = . Gọi CM là đường cao của 
 tam giác SAC. CMR: M là trung điểm của SA và tính thể tích khối tứ diện SMBC theo a. 
 3)(KD – 11) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a, mp(SBC) 
 vuông góc mp(ABC). Biết SB = 2a và . Tính thể tích khối chóp S.ABC và khoảng cách từ 
 điểm B đến mp(SAC) theo a.
 4)(KA – 07) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm 
 trong mp vuông góc với mp đáy. Gọi M, N, P lần lượt là trung điểm của SB, BC, CD. Tính thể tích khối 
 tứ diện CMNP và chứng minh AM vuông góc BP.
 5)(KB-13) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm
 trong mặt phẳng vuông góc với mặt phẳng đáy. Tính theo a thể tính của khối chóp S.ABCD và khoảng
 cách từ điểm A đến mặt phẳng (SCD).
 6) Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a, SA = 2a và SA vuông góc mp(ABC). 
 Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Tính VA.BCNM.
 7) (KA – 09) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, 
 CD = a, góc giữa hai mp(SBC) và (ABCD) bằng 600. Gọi I là trung điểm của cạnh AD. Biết hai 
 mp(SBI) và (SCI) cùng vuông góc với mp(ABCD), tính thể tích khối chóp SABCD theo a. 
 ĐS: 1. 2. 3.,h = 4. 5.,d = 6. 7. 
 PHẦN 2: KHỐI LĂNG TRỤ 
 a. Lăng trụ đứng: Là lăng trụ có cạnh bên vuông góc
 với đáy. Các mặt bên là các hình chữ nhật. Cạnh bên
 bằng đường cao của lăng trụ.
 b. Lăng trụ đều: Là lăng trụ đứng và có đáy là đa 
 giác đều. Các mặt bên của lăng trụ đều là các hình 
 chữ nhật và bằng nhau.
 c. Lăng trụ xiên: Là lăng trụ có các cạnh bên không 
 vuông góc đáy, mặt bên là các hình bình hành
 d. Hình hộp: Là hình lăng trụ có đáy là hình bình hành. 
 - 6 mặt của hình hộp là các hình bình hành.
 - Hai mặt đối diện song song và bằng nhau.
 - Bốn đường chéo của hình hộp đồng quy tại 
 trung điểm của mỗi đường
 1)(TN-12) Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B và BA= BC = a. Góc 
 giữa đường thẳng A’B với mặt phẳng (ABC) bằng 60o. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a. 
 2) Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, BC = , mặt bên 
 (A’BC) hợp với mặt đáy (ABC) một góc 300 .Tính thể tích khối lăng trụ.
3) Cho khối lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều cạnh a, điểm A’ cách đều 3 đỉnh A, B, C, 
 cạnh bên AA’ tạo với mp đáy một góc 600.
 a/ Tính thể tích lăng trụ ABC.A’B’C’.
 b/ CMR: mặt bên BCC’B’ là một hình chữ nhật.
 c/ Tính tổng diện tích các mặt bên của hình lăng trụ ABC.A’B’C’.
4) Cho lăng trụ tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt đáy 
 là 600 và hình chiếu H của điểm A’ trên mp(ABC) trùng với trung điểm của cạch BC.
 a/ Tính thể tích khối tứ diện A’ABC. b/ Tính góc giữa hai mp(ABB’A’) và (ABC).
 5) Cho lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a.
 a/ Tính thể tích khối tứ diện A’BB’C. 
 b/ Mặt phẳng đi qua A’B’ và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Tính thể 
 tích hình chóp CA’B’FE.
6)(KB-11) Cho lăng trụ ABCD.A1B1C1D1 có đáy ABCD là hình chữ nhật, AB = a, AD = a. Hình chiếu 
 vuông góc của điểm A1 trên mp(ABCD) trùng với giao điểm của AC và BD. Góc giữa 2 mp(ADD1A1) và 
 (ABCD) bằng 600. Tính thể tích khối lăng trụ đã cho và khoảng cách từ điểm B1 đến mp(A1BD) theo a.
7) Cho lăng trụ ABC.A’B’C’ có độ dài cạnh bên bằng 2a, đáy ABC là tam giác vuông tại A, AB = a , 
 AC = . Hình chiếu vuông góc của A’ trên mp(ABC) là trung điểm của cạnh BC. Tính theo a thể tích
 khối chóp A’.BCC’B’ và khoảng cách từ B’ đến mp(AA’C’C).
8) (KB- 09) Cho hình lăng trụ tam giác ABC.A’B’C’ có BB’ = a, góc giữa đường thẳng BB’ và mp(ABC) 
 bằng 600, tam giác ABC vuông tại C và BÂC = 600. Hình chiếu vuông góc của điểm B’ lên mp(ABC) 
 trùng với trọng tâm của ABC. Tính thể tích hình chóp A’ABC theo a.
 ĐS: 1, 2, 3, a, c, 4, a, b, 
 5, a, b, 6,, 7, V = a3, h = 8, V = 
 Bài tập rèn luyện. 
 1) Cho chóp tam giác đều S.ABC cạnh đáy bằng a và cạnh bên bằng 2a. Chứng minh rằng chân đường 
 cao kẻ từ S của hình chóp là tâm của tam giác đều ABC. Tính thể tích chóp đều SABC .
 2) Cho hình chóp tứ giác đều S.ABCD có mặt bên hợp với đáy một góc 450 và khoảng cách từ chân đường 
 cao của hình chóp đến mặt bên bằng a. Tính thể tích hình chóp .
 3) Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a. Mặt bên SAB là tam giác đều nằm 
 trong mặt phẳng vuông góc với đáy ABCD. Chứng minh rằng chân đường cao khối chóp trùng với 
 trung điểm cạnh AB. Tính thể tích khối chóp SABCD. 
 4) Cho hình chóp S.ABC có ∆ABC vuông cân ở B,, SA vuông góc với đáy ABC ,
 Gọi G là trọng tâm tam giác ABC, mặt phẳng () qua AG và song song với BC cắt SC, SB lần lượt tại 
 M, N. Tính thể tích của khối chóp S.AMN 
 5) Cho hình chóp tam giác S.ABC có AB = 5a, BC = 6a, CA = 7a. Các mặt bên SAB, SBC, SCA tạo với 
 đáy một góc 600. Tính thể tích khối chóp S.ABC theo a. 
 6) Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA = a, SB = a và mp(SAB) vuông góc với 
 mp đáy. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Tính thể tích của khối chóp S.BMDN 
 7) Cho hình chóp S.ABCD đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mp 
 vuông góc với đáy. Gọi E, F lần lượt là trọng tâm các tam giác ABD và SBC. Tính thể tích của khối tứ
 diện CDEF và chứng minh mp(SAF) vuông góc mp(SDE).
 8) Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a , hình chiếu vuông góc của A’ lên 
 mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC, cạnh A’A hợp với mặt đáy (ABC) một góc
 300. Tính thể tích khối lăng trụ.
 9) Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Gọi M,N lần lượt là trung 
 điểm của các cạnh BC, CC’. Tính thể tích tứ diện AA’MN và khoảng cách từ điểm A’ đến mp(AMN).
10) (KD- 09) Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, AA’ = 2a,
 A’C = 3a. Gọi M là trung điểm của đoạn thẳng A’C’, I là giao điểm của AM và A’C. Tính theo a thể 
 tích khối tứ diện IABC và khoảng cách từ điểm A đến mp(IBC).
11) (KD -12) Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông, A’AC vuông cân, A’C = a. 
 Tính thể tích khối tứ diện ABB’C’ và khoảng cách từ điểm A đến mp(BCD’) theo a. 
12) Cho lăng trụ ABC A'B'C' có đáy ABC là tam giác đều với tâm O. Cạnh bên CC' = a hợp với đáy ABC
 một góc 600 và C' có hình chiếu trên ABC trùng với O. Chứng minh rằng AA'B'B là hình chữ nhật.
 Tính diện tích AA'B'B. Tính thể tích lăng trụ ABCA'B'C'. 
 ĐS : 1. 2. 3. 4. 5. 6. 7. 8, 
 9, ,h = 10, , d = 11, 12,